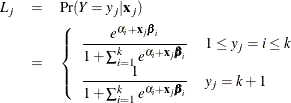The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
If you use the events/trials syntax, each observation is split into two observations. One has the response value 1 with a frequency equal to the value of the events variable. The other observation has the response value 2 and a frequency equal to the value of (trials – events). These two observations have the same explanatory variable values and the same WEIGHT values as the original observation.
For either the single-trial or the events/trials syntax, let j index all observations. In other words, for the single-trial syntax, j indexes the actual observations. And, for the events/trials syntax, j indexes the observations after splitting (as described previously). If your data set has 30 observations and you use the single-trial syntax, j has values from 1 to 30; if you use the events/trials syntax, j has values from 1 to 60.
Suppose the response variable in a cumulative response model can take on the ordered values ![]() , where k is an integer
, where k is an integer ![]() . The likelihood for the jth observation with ordered response value
. The likelihood for the jth observation with ordered response value ![]() and explanatory variables vector ( row vectors)
and explanatory variables vector ( row vectors) ![]() is given by
is given by
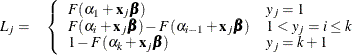
where ![]() is the logistic, normal, or extreme-value distribution function;
is the logistic, normal, or extreme-value distribution function; ![]() are ordered intercept parameters; and
are ordered intercept parameters; and ![]() is the slope parameter vector.
is the slope parameter vector.
For the generalized logit model, letting the ![]() st level be the reference level, the intercepts
st level be the reference level, the intercepts ![]() are unordered and the slope vector
are unordered and the slope vector ![]() varies with each logit. The likelihood for the jth observation with ordered response value
varies with each logit. The likelihood for the jth observation with ordered response value ![]() and explanatory variables vector
and explanatory variables vector ![]() (row vectors) is given by
(row vectors) is given by