Confidence Limits :: SAS/STAT(R) 13.1 User's Guide

Confidence Limits

Subsections:

MLS Confidence Limits
Generalized Confidence Limits

When no exact confidence limits exist, it is common practice to use approximate confidence limits. Two such approximations are the modified large-sample (MLS) method and the generalized confidence limit (GCL) method as discussed in Burdick, Borror, and Montgomery (2005). When analyzing a balanced one-way or two-way design, if you specify the CL= option with METHOD=TYPE1 or GRR, the VARCOMP procedure computes confidence limits by using either the MLS method (the default) or the GCL method. Generalized confidence limits are obtained by specifying the CL=GCL option in the MODEL statement.

MLS Confidence Limits

The method of MLS confidence limits was first introduced by Graybill and Wang (1980). It starts with approximate large-sample confidence limits; then it modifies the limits to be exact under certain parameter conditions.

For a balanced two-way crossed random model with interaction, formulas for the MLS method are given in Table 105.6. See Burdick, Borror, and Montgomery (2005) for the formulas for one-way or balanced two-way with no interaction models.

Confidence limits for parameters such as variances and their ratios might not contain the corresponding point estimates, because negative confidence bounds are increased to zero.

Table 105.6: 100( $1-\alpha$ )% MLS Confidence Limits

Parameter	Lower Bound	Upper Bound
$\mu _ y$	$\bar{y}_{\cdot \cdot \cdot } - C\sqrt {\frac{K}{por}}$	$\bar{y}_{\cdot \cdot \cdot } + C\sqrt {\frac{K}{por}}$
$\gamma _ P$	$\hat{\gamma }_ P - \sqrt {V_{LP}}/(or)$	$\hat{\gamma }_ P + \sqrt {V_{UP}}/(or)$
$\gamma _ M$	$\hat{\gamma }_ M - \sqrt {V_{LM}}/(pr)$	$\hat{\gamma }_ M + \sqrt {V_{UM}}/(pr)$
$\gamma _ y$	$\hat{\gamma }_ y - \sqrt {V_{LT}}/(por)$	$\hat{\gamma }_ y + \sqrt {V_{UT}}/(por)$
$\gamma _ R$	$L_ R$	$U_ R$
$\rho _ P$	$L_ R/(1 + L_ R)$	$U_ R/(1 + U_ R)$
$\rho _ M$	$1/(1 + U_ R)$	$1/(1 + L_ R)$

The terms in Table 105.6 are defined as follows:

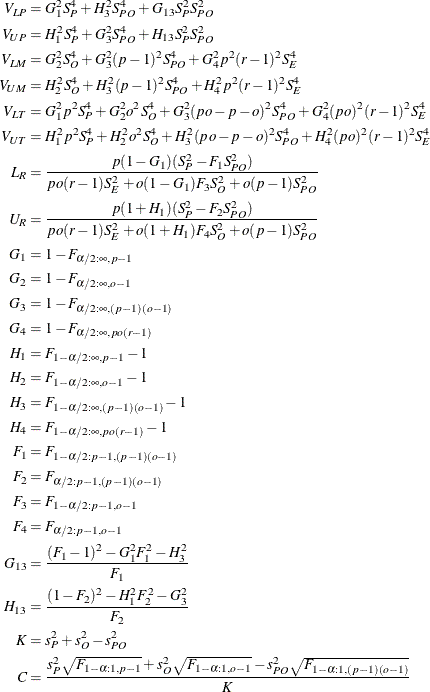
$\begin{align*} V_{LP} & = G^2_1 S^4_ P + H^2_3 S^4_{PO} + G_{13} S^2_ P S^2_{PO} \\ V_{UP} & = H^2_1 S^4_ P + G^2_3 S^4_{PO} + H_{13} S^2_ P S^2_{PO} \\ V_{LM} & = G^2_2 S^4_ O + G^2_3(p-1)^2 S^4_{PO} + G^2_4 p^2 (r-1)^2 S^4_ E \\ V_{UM} & = H^2_2 S^4_ O + H^2_3(p-1)^2 S^4_{PO} + H^2_4 p^2 (r-1)^2 S^4_ E \\ V_{LT} & = G^2_1 p^2 S^4_ P + G^2_2 o^2 S^4_ O + G^2_3(po-p-o)^2 S^4_{PO} + G^2_4(po)^2 (r-1)^2 S^4_ E \\ V_{UT} & = H^2_1 p^2 S^4_ P + H^2_2 o^2 S^4_ O + H^2_3(po-p-o)^2 S^4_{PO} + H^2_4(po)^2 (r-1)^2 S^4_ E \\ L_ R & = \frac{p(1-G_1)(S^2_ P - F_1 S^2_{PO})}{ po(r-1)S^2_ E + o(1-G_1)F_3 S^2_ O + o(p-1)S^2_{PO}} \\ U_ R & = \frac{p(1+H_1)(S^2_ P - F_2 S^2_{PO})}{ po(r-1)S^2_ E + o(1+H_1)F_4 S^2_ O + o(p-1)S^2_{PO}} \\ G_1 & = 1 - F_{\alpha /2:\infty ,p-1} \\ G_2 & = 1 - F_{\alpha /2:\infty ,o-1} \\ G_3 & = 1 - F_{\alpha /2:\infty ,(p-1)(o-1)} \\ G_4 & = 1 - F_{\alpha /2:\infty ,po(r-1)} \\ H_1 & = F_{1-\alpha /2:\infty ,p-1} - 1 \\ H_2 & = F_{1-\alpha /2:\infty ,o-1} - 1 \\ H_3 & = F_{1-\alpha /2:\infty ,(p-1)(o-1)} - 1 \\ H_4 & = F_{1-\alpha /2:\infty ,po(r-1)} - 1 \\ F_1 & = F_{1-\alpha /2:p-1,(p-1)(o-1)} \\ F_2 & = F_{\alpha /2:p-1,(p-1)(o-1)} \\ F_3 & = F_{1-\alpha /2:p-1,o-1} \\ F_4 & = F_{\alpha /2:p-1,o-1} \\ G_{13} & = \frac{(F_1 - 1)^2 - G^2_1 F^2_1 - H^2_3}{F_1} \\ H_{13} & = \frac{(1 - F_2)^2 - H^2_1 F^2_2 - G^2_3}{F_2} \\ K & = s^2_ P + s^2_ O - s^2_{PO} \\ C & = \frac{s^2_ P\sqrt {F_{1-\alpha :1,p-1}} + s^2_ O\sqrt {F_{1-\alpha :1,o-1}} - s^2_{PO}\sqrt {F_{1-\alpha :1,(p-1)(o-1)}}}{K} \\ \end{align*}$

The symbol $F_{\alpha :\mi {df1},\mi {df2}}$ represents the percentile of an F distribution with df1 and df2 degrees of freedom and area $\alpha$ to the left.

Generalized Confidence Limits

The method of generalized confidence limits was first introduced by Weerahandi (1993). The 100(1- $\alpha$ )% generalized confidence limits are determined as follows:

Initialize the random number generator with the seed. The seed value is specified by the SEED= option.
Sample N generalized pivot quantities (GPQ), defined to have a distribution that is independent of the parameters under study. The value N is specified by the NSAMPLE= option.
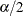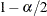Define the lower and upper limits as the $\alpha /2$ and $1-\alpha /2$ quantiles of the sampled GPQ values.

Formulas for generalized confidence limits are given in Table 105.7, where Z denotes a standard normal random variable and $W_1, W_2, W_3,$ and $W_4$ denote jointly independent chi-square random variables that are independent of Z with degrees of freedom $p-1, o-1, (p-1)(o-1)$ and $po(r-1)$ , respectively. The value of $\epsilon$ in Table 105.7 is specified by the EPSILON= option.

Table 105.7: 100( $1-\alpha$ )% Generalized Confidence Limits

Parameter	GPQ
$\mu _ y$	$\bar{y}_{\cdot \cdot \cdot } - Z\sqrt {\max \left[ \epsilon , \frac{(p-1)s^2_ p}{porW_1} + \frac{(o-1)s^2_ O}{porW_2} - \frac{(p-1)(o-1)s^2_{PO}}{porW_3}\right]}$
$\gamma _ P$	$\max \left[ 0,\frac{(p-1)s^2_ p}{orW_1} - \frac{(p-1)(o-1)s^2_{po}}{prW_3}\right]$
$\gamma _ M$	$\frac{(o-1)s^2_ o}{prW_2} + \frac{(p-1)^2(0-1)s^2_ po}{prW_3} + \frac{po(r-1)^2s^2_ E}{rW_4}$
$\gamma _ y$	$\frac{(p-1)s^2_ p}{orW_1} + \frac{(o-1)s^2_ O}{prW_2} + \frac{(po-p-o)(p-1)(o-1)s^2_{PO}}{porW_3} + \frac{po(r-1)^2s^2_ E}{rW_4}$
$\gamma _ R$	$\frac{\mbox{GPQ}(\gamma _ P)}{\mbox{GPQ}(\gamma _ M)}$

In general, the GCL method provides a more accurate confidence interval with a shorter interval width than the MLS method. However, the greater accuracy comes at the cost of being somewhat nondeterministic, because of the reliance on simulation.

The VARCOMP Procedure