The CALIS Procedure
-
Overview
-
Getting Started
-
SyntaxClasses of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
-
DetailsInput Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
-
ExamplesEstimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
- References
While fitting structural equation models is mostly a confirmatory analytic procedure, it does not prevent you from exploring what might have been a better model given the data. After fitting your theoretical structural equation model, you might want to modify the original model in order to do one of the following:
-
add free parameters to improve the model fit significantly
-
reduce the number of parameters without affecting the model fit too much
The first kind of model modification can be achieved by using the Lagrange multiplier (LM) test indices. Parameters that have the largest LM indices would increase the model fit the most. In general, adding more parameters to your model improves the overall model fit, as measured by those absolute or standalone fit indices (see the section Overall Model Fit Indices for more details). However, adding parameters liberally makes your model more prone to sampling errors. It also makes your model more complex and less interpretable in most cases. A disciplined use of LM test indices is highly recommended. In addition to the model fit improvement indicated by the LM test indices, you should also consider the theoretical significance when adding particular parameters. See Example 29.28 for an illustration of the use of LM test indices for improving model fit.
The second kind of model modification can be achieved by using the Wald statistics. Parameters that are not significant in your model may be removed from the model without affecting the model fit too much. In general, removing parameters from your model decreases the model fit, as measured by those absolute or standalone fit indices (see the section Overall Model Fit Indices for more details). However, for just a little sacrifice in model fit, removing non-significant parameters increases the simplicity and precision of your model, which is the virtue that any modeler should look for.
Whether adding parameters by using the LM test indices or removing unnecessary parameters by the Wald statistics, you should not treat your modified model as if it were your original hypothesized model. That is, you should not publish your modified model as if it were hypothesized a priori. It is perfectly fine to use modification indices to gain additional insights for future research. But if you want to publish your modified model together with your original model, you should report the modification process that leads to your modified model. Theoretical justifications of the modified model should be supplemented if you want to make strong statements to support your modified model. Whenever possible, the best practice is to show reasonable model fit of the modified model with new data.
To modify your model either by LM test indices or Wald statistics, you can use the MODIFICATION or MOD option in the PROC CALIS statement. To customize the LM tests by setting specific regions of parameters, you can use the LMTESTS statements. PROC CALIS computes and displays the following default set of modification indices:
-
univariate Lagrange multiplier (LM) test indices for parameters in the modelThese are second-order approximations of the decrease in the
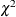value that would result from allowing the fixed parameter values in the model to be freed to estimate. LM test indices are ranked within their own parameter regions in the model. The ones
that suggest greatest model improvements (that is, greatest 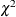drop) are ranked first. Depending on the type of your model, the set of possible parameter regions varies. For example, in
a RAM model, modification indices are ranked in three different parameter regions for the covariance structures: path coefficients,
variances of and covariances among exogenous variables, and the error variances and covariances. In addition to the value
of the Lagrange multiplier, the corresponding p-value (df = 1) and the approximate change of the parameter value are displayed.
If you use the LMMAT option in the LMTESTS statement, LM test indices are shown as elements in model matrices. Not all elements in a particular model matrix will have LM test indices. Elements that are already free parameters in the model do not have LM test indices. Instead, the parameter names are shown. Elements that are model restricted values (for example, direct path from a variable to itself must be zero) are labeled
Excludedin the matrix output. When you customize your own regions of LM tests, some elements might also be excluded from a custom set of LM tests. These elements are also labeled asExcludedin the matrix output. If an LM test for freeing a parameter would result in a singular information matrix, the corresponding element in the matrix is labeled asSingular. -
univariate Lagrange multiplier test indices for releasing equality constraintsThese are second-order approximations of the decrease in the
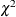value that would result from the release of equality constraints. Multiple equality constraints containing n > 2 parameters are tested successively in n steps, each assuming the release of one of the equality-constrained parameters. The expected change of the parameter values
of the separated parameter and the remaining parameter cluster are displayed, too.
-
univariate Lagrange multiplier test indices for releasing active boundary constraintsThese are second-order approximations of the decrease in the
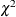value that would result from the release of the active boundary constraints specified in the BOUNDS
statement.
-
stepwise multivariate Wald statistics for constraining free parameters to 0These are second-order approximations of the increases in
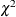value that would result from constraining free parameters to zero in a stepwise fashion. In each step, the parameter that
would lead to the smallest increase in the multivariate 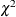value is set to 0. Besides the multivariate 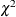value and its p-value, the univariate increments are also displayed. The process stops when the univariate p-value is smaller than the specified value in the SLMW=
option, of which the default value is 0.05.
All of the preceding tests are approximations. You can often obtain more accurate tests by actually fitting different models and computing likelihood ratio tests. For more details about the Wald and the Lagrange multiplier test, see MacCallum (1986), Buse (1982), Bentler (1986), or Lee (1985). Note that relying solely on the LM tests to modify your model can lead to unreliable models that capitalize purely on sampling errors. See MacCallum, Roznowski, and Necowitz (1992) for the use of LM tests.
For large model matrices, the computation time for the default modification indices can considerably exceed the time needed for the minimization process.
The modification indices are not computed for unweighted least squares or diagonally weighted least squares estimation.