The CLUSTER Procedure
In some biological applications, the organisms that are being clustered can be at different stages of growth. Unless it is the growth process itself that is being studied, differences in size among such organisms are not of interest. Therefore, distances among organisms should be computed in such a way as to control for differences in size while retaining information about differences in shape.
If coordinate data are measured on an interval scale, you can control for size by subtracting a measure of the overall size of each observation from each data item. For example, if no other direct measure of size is available, you could subtract the mean of each row of the data matrix, producing a row-centered coordinate matrix. An easy way to subtract the mean of each row is to use PROC STANDARD on the transposed coordinate matrix:
proc transpose data= coordinate-datatype; run; proc standard m=0; run; proc transpose out=row-centered-coordinate-data; run;
Another way to remove size effects from interval-scale coordinate data is to do a principal component analysis and discard the first component (Blackith and Reyment, 1971).
If the data are measured on a ratio scale, you can control for size by dividing each observation by a measure of overall size; in this case, the geometric mean is a more natural measure of size than the arithmetic mean. However, it is often more meaningful to analyze the logarithms of ratio-scaled data, in which case you can subtract the arithmetic mean after taking logarithms. You must also consider the dimensions of measurement. For example, if you have measures of both length and weight, you might need to cube the measures of length or take the cube root of the weights. Various other complications can also arise in real applications, such as different growth rates for different parts of the body (Sneath and Sokal, 1973).
Issues of size and shape are pertinent to many areas besides biology (for example, Hamer and Cunningham 1981). Suppose you have data consisting of subjective ratings made by several different raters. Some raters tend to give higher overall ratings than other raters. Some raters also tend to spread out their ratings over more of the scale than other raters. If it is impossible for you to adjust directly for rater differences, then distances should be computed in such a way as to control for differences both in size and variability. For example, if the data are considered to be measured on an interval scale, you can subtract the mean of each observation and divide by the standard deviation, producing a row-standardized coordinate matrix. With some clustering methods, analyzing squared Euclidean distances from a row-standardized coordinate matrix is equivalent to analyzing the matrix of correlations among rows, since squared Euclidean distance is an affine transformation of the correlation (Hartigan; 1975, p. 64).
If you do an analysis of row-centered or row-standardized data, you need to consider whether the columns (variables) should be standardized before centering or standardizing the rows, after centering or standardizing the rows, or both before and after. If you standardize the columns after standardizing the rows, then strictly speaking you are not analyzing shape because the profiles are distorted by standardizing the columns; however, this type of double standardization might be necessary in practice to get reasonable results. It is not clear whether iterating the standardization of rows and columns can be of any benefit.
The choice of distance or correlation measure should depend on the meaning of the data and the purpose of the analysis. Simulation studies that compare distance and correlation measures are useless unless the data are generated to mimic data from your field of application. Conclusions drawn from artificial data cannot be generalized, because it is possible to generate data such that distances that include size effects work better or such that correlations work better.
You can standardize the rows of a data set by using a DATA step or by using the TRANSPOSE and STANDARD procedures. You can also use PROC TRANSPOSE and then have PROC CORR create a TYPE=CORR data set containing a correlation matrix. If you want to analyze a TYPE=CORR data set with PROC CLUSTER, you must use a DATA step to perform the following steps:
-
Set the data set TYPE= to DISTANCE.
-
Convert the correlations to dissimilarities by computing
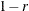 ,
, 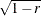 ,
, 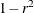 , or some other decreasing function.
, or some other decreasing function.
-
Delete observations for which the variable
_TYPE_does not have the value ’CORR’.
