The DISCRIM Procedure
In the following discussion, let

The amount of temporary storage required depends on the discriminant method used and the options specified. The least amount of temporary storage in bytes needed to process the data is approximately
A parametric method (METHOD=NORMAL) requires an additional temporary memory of ![]() bytes. When you specify the CROSSVALIDATE option, this temporary storage must be increased by
bytes. When you specify the CROSSVALIDATE option, this temporary storage must be increased by ![]() bytes. When a nonparametric method (METHOD=NPAR) is used, an additional temporary storage of
bytes. When a nonparametric method (METHOD=NPAR) is used, an additional temporary storage of ![]() bytes is needed if you specify METRIC=FULL to evaluate the distances.
bytes is needed if you specify METRIC=FULL to evaluate the distances.
With the MANOVA option, the temporary storage must be increased by ![]() bytes. The CANONICAL option requires a temporary storage of
bytes. The CANONICAL option requires a temporary storage of ![]() bytes. The POSTERR option requires a temporary storage of
bytes. The POSTERR option requires a temporary storage of ![]() bytes. Additional temporary storage is also required for classification summary and for each output data set.
bytes. Additional temporary storage is also required for classification summary and for each output data set.
Consider the following statements:
proc discrim manova; class gp; var x1 x2 x3; run;
If the CLASS variable gp has a length of 8 and the input data set contains two class levels, the procedure requires a temporary storage of 1992 bytes.
This includes 1104 bytes for processing data, 480 bytes for using a parametric method, and 408 bytes for specifying the MANOVA
option.
The following factors determine the time requirements of discriminant analysis:
-
The time needed for reading the data and computing covariance matrices is proportional to
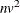 . PROC DISCRIM must also look up each class level in the list. This is faster if the data are sorted by the CLASS variable.
The time for looking up class levels is proportional to a value ranging from n to
. PROC DISCRIM must also look up each class level in the list. This is faster if the data are sorted by the CLASS variable.
The time for looking up class levels is proportional to a value ranging from n to 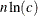 .
.
-
The time for inverting a covariance matrix is proportional to
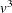 .
.
-
With a parametric method, the time required to classify each observation is proportional to
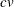 for a linear discriminant function and
for a linear discriminant function and 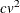 for a quadratic discriminant function. When you specify the CROSSVALIDATE option, the discriminant function is updated for
each observation in the classification. A substantial amount of time is required.
for a quadratic discriminant function. When you specify the CROSSVALIDATE option, the discriminant function is updated for
each observation in the classification. A substantial amount of time is required.
-
With a nonparametric method, the data are stored in a tree structure (Friedman, Bentley, and Finkel, 1977). The time required to organize the observations into the tree structure is proportional to
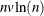 . The time for performing each tree search is proportional to
. The time for performing each tree search is proportional to 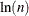 . When you specify the normal KERNEL= option, all observations in the training sample contribute to the density estimation
and more computer time is needed.
. When you specify the normal KERNEL= option, all observations in the training sample contribute to the density estimation
and more computer time is needed.
-
The time required for the canonical discriminant analysis is proportional to
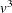 .
.
Each of the preceding factors has a different machine-dependent constant of proportionality.
