The GLMSELECT Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Model-Selection MethodsModel Selection IssuesCriteria Used in Model Selection MethodsCLASS Variable Parameterization and the SPLIT OptionMacro Variables Containing Selected ModelsUsing the STORE StatementBuilding the SSCP MatrixModel AveragingUsing Validation and Test DataCross ValidationExternal Cross ValidationScreeningDisplayed OutputODS Table NamesODS Graphics
Model-Selection MethodsModel Selection IssuesCriteria Used in Model Selection MethodsCLASS Variable Parameterization and the SPLIT OptionMacro Variables Containing Selected ModelsUsing the STORE StatementBuilding the SSCP MatrixModel AveragingUsing Validation and Test DataCross ValidationExternal Cross ValidationScreeningDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
This example shows how you can use multimember effects to build predictive models. It also demonstrates several features of the OUTDESIGN= option in the PROC GLMSELECT statement.
The simulated data for this example describe a two-week summer tennis camp. The tennis ability of each camper was assessed and ratings were assigned at the beginning and end of the camp. The camp consisted of supervised group instruction in the mornings with a number of different options in the afternoons. Campers could elect to participate in unsupervised practice and play. Some campers paid for one or more individual lessons from 30 to 90 minutes in length, focusing on forehand and backhand strokes and volleying. The aim of this example is to build a predictive model for the rating improvement of each camper based on the times the camper spent doing each activity and several other variables, including the age, gender, and initial rating of the camper.
The following statements produce the TennisCamp data set:
data TennisCamp;
length forehandCoach $6 backhandCoach $6 volleyCoach $6 gender $1;
input forehandCoach backhandCoach volleyCoach tLessons tPractice tPlay
gender inRating nPastCamps age tForehand tBackhand tVolley
improvement;
label forehandCoach = "Forehand lesson coach"
backhandCoach = "Backhand lesson coach"
volleyCoach = "Volley lesson coach"
tForehand = "time (1/2 hours) of forehand lesson"
tBackhand = "time (1/2 hours) of backhand lesson"
tVolley = "time (1/2 hours) of volley lesson"
tLessons = "time (1/2 hours) of all lessons"
tPractice = "total practice time (hours)"
tPlay = "total play time (hours)"
nPastCamps = "Number of previous camps attended"
age = "age (years)"
inRating = "Rating at camp start"
improvement = "Rating improvement at end of camp";
datalines;
. . Tom 1 30 19 f 44 0 13 0 0 1 6
Greg . . 2 12 33 f 48 2 15 2 0 0 14
. . Mike 2 12 24 m 53 0 15 0 0 2 13
. Mike . 1 12 28 f 48 0 13 0 1 0 11
. Bruna . 2 13 34 f 57 0 16 0 2 0 12
... more lines ...
. . . 0 12 38 m 47 1 15 0 0 0 8
Greg Tom Tom 6 3 41 m 48 2 15 2 1 3 19
. Greg Mike 5 30 16 m 52 0 13 0 2 3 18
;
A multimember effect (see the section EFFECT Statement in Chapter 19: Shared Concepts and Topics) is appropriate for modeling the effect of coaches on the campers’ improvement, because campers might have worked with multiple coaches. Furthermore, since the time a coach spent with each camper varies, it is appropriate to use these times to weight each coach’s contribution in the multimember effect. It is also important not to exclude campers from the analysis if they did not receive any individual instruction. You can accomplish all these goals by using a multimember effect defined as follows:
class forehandCoach backhandCoach volleyCoach;
effect coach = MM(forehandCoach backhandCoach volleyCoach/ noeffect
weight=(tForehand tBackhand tVolley));
Based on similar previous studies, it is known that the time spent practicing should not be included linearly, because there are diminishing returns and perhaps even counterproductive effects beyond about 25 hours. A spline effect with a single knot at 25 provides flexibility in modeling effect of practice time.
The following statements use PROC GLMSELECT to select effects for the model.
proc glmselect data=TennisCamp outdesign=designCamp;
class forehandCoach backhandCoach volleyCoach gender;
effect coach = mm(forehandCoach backhandCoach volleyCoach / noeffect
details weight=(tForehand tBackhand tVolley));
effect practice = spline(tPractice/knotmethod=list(25) details);
model improvement = coach practice tLessons tPlay age gender
inRating nPastCamps;
run;
Output 48.4.1 shows the class level and MM level information. The levels of the constructed MM effect are the union of the levels of its constituent classification variables. The MM level information is not displayed by default—you request this table by specifying the DETAILS suboption in the relevant EFFECT statement.
Output 48.4.1: Levels of MM EFFECT Coach
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| forehandCoach | 5 | Bruna Elaine Greg Mike Tom |
| backhandCoach | 5 | Bruna Elaine Greg Mike Tom |
| volleyCoach | 5 | Andy Bruna Greg Mike Tom |
| gender | 2 | f m |
| Level Details for MM Effect coach | |
|---|---|
| Levels | Values |
| 6 | Andy Bruna Elaine Greg Mike Tom |
Output 48.4.2 shows the parameter estimates for the selected model. You can see that the constructed multimember effect coach and the spline effect practice are both included in the selected model. All coaches provided benefit (all the parameters of the multimember effect coach are positive), with Greg and Mike being the most effective.
Output 48.4.2: Parameter Estimates
| Parameter Estimates | ||||
|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value |
| Intercept | 1 | 0.379873 | 0.513431 | 0.74 |
| coach Andy | 1 | 1.444370 | 0.318078 | 4.54 |
| coach Bruna | 1 | 1.446063 | 0.110179 | 13.12 |
| coach Elaine | 1 | 1.312290 | 0.281877 | 4.66 |
| coach Greg | 1 | 3.042828 | 0.112256 | 27.11 |
| coach Mike | 1 | 2.840728 | 0.121166 | 23.45 |
| coach Tom | 1 | 1.248946 | 0.115266 | 10.84 |
| practice 1 | 1 | 2.538938 | 1.015772 | 2.50 |
| practice 2 | 1 | 3.837684 | 1.104557 | 3.47 |
| practice 3 | 1 | 2.574775 | 0.930816 | 2.77 |
| practice 4 | 1 | -0.034747 | 0.717967 | -0.05 |
| practice 5 | 0 | 0 | . | . |
| tPlay | 1 | 0.139409 | 0.023043 | 6.05 |
Suppose you want to examine regression diagnostics for the selected model. PROC GLMSELECT does not support such diagnostics, so you might want to use the REG procedure to produce these diagnostics. You can overcome the difficulty that PROC REG does not support CLASS and EFFECT statements by using the OUTDESIGN= option in the PROC GLMSELECT statement to obtain the design matrix that you can use as an input data set for further analysis with other SAS procedures.
The following statements use PROC PRINT to produce Output 48.4.3, which shows the first five observations of the design matrix designCamp.
proc print data=designCamp(obs=5); run;
Output 48.4.3: First Five Observations of the designCamp Data Set
| Obs | Intercept | coach_Andy | coach_Bruna | coach_Elaine | coach_Greg | coach_Mike | coach_Tom | tPlay | practice_1 | practice_2 | practice_3 | practice_4 | practice_5 | improvement |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 19 | 0.00000 | 0.00136 | 0.05077 | 0.58344 | 0.36443 | 6 |
| 2 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 33 | 0.20633 | 0.50413 | 0.25014 | 0.03940 | 0.00000 | 14 |
| 3 | 1 | 0 | 0 | 0 | 0 | 2 | 0 | 24 | 0.20633 | 0.50413 | 0.25014 | 0.03940 | 0.00000 | 13 |
| 4 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 28 | 0.20633 | 0.50413 | 0.25014 | 0.03940 | 0.00000 | 11 |
| 5 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 34 | 0.16228 | 0.49279 | 0.29088 | 0.05405 | 0.00000 | 12 |
To facilitate specifying the columns of the design matrix corresponding to the selected model, you can use the macro variable
named _GLSMOD that PROC GLMSELECT creates whenever you specify the OUTDESIGN= option. The following statements use PROC REG to produce
a panel of regression diagnostics corresponding to the model selected by PROC GLMSELECT.
ods graphics on; proc reg data=designCamp; model improvement = &_GLSMOD; quit; ods graphics off;
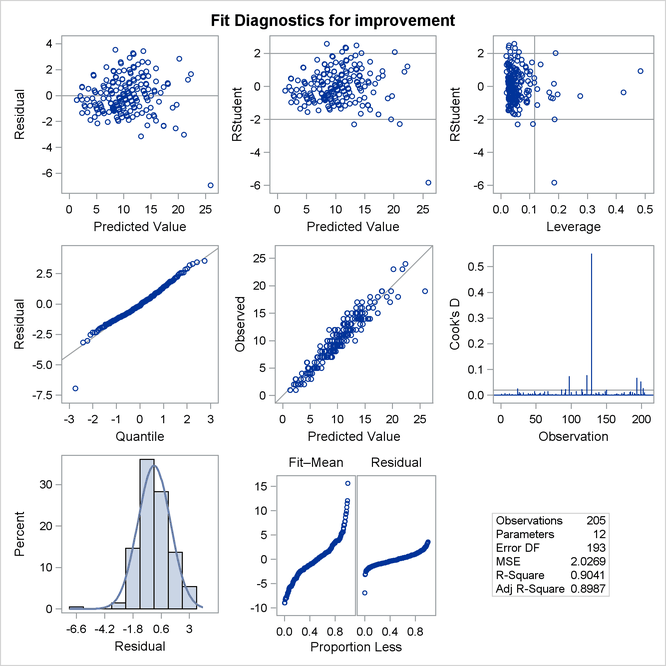
The regression diagnostics shown in Output 48.4.4 indicate a reasonable model. However, they also reveal the presence of one large outlier and several influential observations that you might want to investigate.
Sometimes you might want to use subsets of the columns of the design matrix. In such cases, it might be convenient to produce a design matrix with generic names for the columns. You might also want a design matrix containing the columns corresponding to the full model that you specify in the MODEL statement. By default, the design matrix includes only the columns that correspond to effects in the selected model. The following statements show how to do this.
proc glmselect data=TennisCamp
outdesign(fullmodel prefix=parm names)=designCampGeneric;
class forehandCoach backhandCoach volleyCoach gender;
effect coach = mm(forehandCoach backhandCoach volleyCoach / noeffect
details weight=(tForehand tBackhand tVolley));
effect practice = spline(tPractice/knotmethod=list(25) details);
model improvement = coach practice tLessons tPlay age gender
inRating nPastCamps;
run;
The PREFIX=parm suboption of the OUTDESIGN= option specifies that columns in the design matrix be given the prefix parm with a trailing index. The NAMES suboption requests the table in Output 48.4.5 that associates descriptive labels with the names of columns in the design matrix. Finally, the FULLMODEL suboption specifies
that the design matrix include columns corresponding to all effects specified in the MODEL
statement.
Output 48.4.5: Descriptive Names of Design Matrix Columns
| Parameter Names | |
|---|---|
| Name | Parameter |
| parm1 | Intercept |
| parm2 | coach Andy |
| parm3 | coach Bruna |
| parm4 | coach Elaine |
| parm5 | coach Greg |
| parm6 | coach Mike |
| parm7 | coach Tom |
| parm8 | practice 1 |
| parm9 | practice 2 |
| parm10 | practice 3 |
| parm11 | practice 4 |
| parm12 | practice 5 |
| parm13 | tLessons |
| parm14 | tPlay |
| parm15 | age |
| parm16 | gender f |
| parm17 | gender m |
| parm18 | inRating |
| parm19 | nPastCamps |
The following statements produce Output 48.4.6, displaying the first five observations of the designCampGeneric data set:
proc print data=designCampGeneric(obs=5); run;
Output 48.4.6: First Five Observations of designCampGeneric Data Set
| Obs | parm1 | parm2 | parm3 | parm4 | parm5 | parm6 | parm7 | parm8 | parm9 | parm10 | parm11 | parm12 | parm13 | parm14 | parm15 | parm16 | parm17 | parm18 | parm19 | improvement |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0.00000 | 0.00136 | 0.05077 | 0.58344 | 0.36443 | 1 | 19 | 13 | 1 | 0 | 44 | 0 | 6 |
| 2 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0.20633 | 0.50413 | 0.25014 | 0.03940 | 0.00000 | 2 | 33 | 15 | 1 | 0 | 48 | 2 | 14 |
| 3 | 1 | 0 | 0 | 0 | 0 | 2 | 0 | 0.20633 | 0.50413 | 0.25014 | 0.03940 | 0.00000 | 2 | 24 | 15 | 0 | 1 | 53 | 0 | 13 |
| 4 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0.20633 | 0.50413 | 0.25014 | 0.03940 | 0.00000 | 1 | 28 | 13 | 1 | 0 | 48 | 0 | 11 |
| 5 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 0.16228 | 0.49279 | 0.29088 | 0.05405 | 0.00000 | 2 | 34 | 16 | 1 | 0 | 57 | 0 | 12 |