Shared Concepts and Topics
This example uses data from Kutner (1974, p. 98) to illustrate a two-way analysis of variance. The original data source is Afifi and Azen (1972, p. 166). The following statements create the data set a:
data a;
input drug disease @;
do i=1 to 6;
input y @;
output;
end;
datalines;
1 1 42 44 36 13 19 22
1 2 33 . 26 . 33 21
1 3 31 -3 . 25 25 24
2 1 28 . 23 34 42 13
2 2 . 34 33 31 . 36
2 3 3 26 28 32 4 16
3 1 . . 1 29 . 19
3 2 . 11 9 7 1 -6
3 3 21 1 . 9 3 .
4 1 24 . 9 22 -2 15
4 2 27 12 12 -5 16 15
4 3 22 7 25 5 12 .
;
In the following statements, PROC GENMOD fits two classification variables and their interaction to Y. The first EFFECTPLOT statement displays the default graphic, which plots the predicted values against Disease for each of the three Drug levels. The OBS
option also displays the observations in the plot. The second EFFECTPLOT statement modifies the default to plot the predicted
values against Drug for each of the three Disease levels. The CLM
option is specified to produce 95% confidence bars for the means.
ods graphics on; proc genmod data=a; class drug disease; model y=disease drug disease*drug / d=n; effectplot / obs; effectplot interaction(sliceby=disease) / clm; run; ods graphics off;
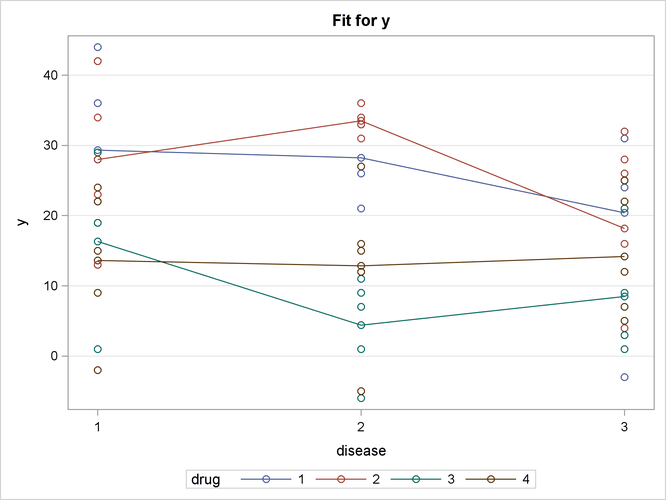
In Output 19.2.1, the default interaction plot is produced, and the observations are also displayed. From this plot, you can compare the performance of the drugs for a given disease. The predicted values are connected with a line to provide something for your eye to follow; obviously a line has no intrinsic meaning in this graphic. Drugs 3 and 4 are consistently outperformed by the first two drugs.
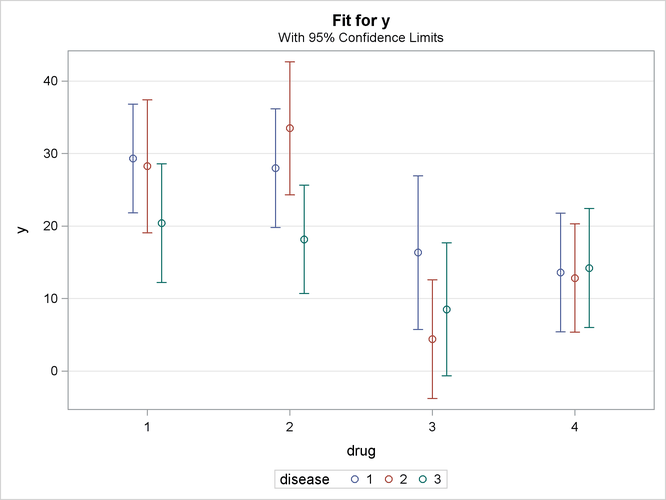
By default, the first classification variable is displayed on the X axis and the second classification variable is used for grouping. Specifying the SLICEBY= DISEASE option in the second EFFECTPLOT statement does the reverse: it displays the classification variable that has the most levels on the X axis, and slices by fewer levels, resulting in a more readable display. Output 19.2.2 shows how well a given drug performs for each disease.
In the following statements, the BOX
plot-type is requested to display box plots of the predictions by each combination of drug and disease. The second EFFECTPLOT statement
displays the same information by using an INTERACTION
plot-type and specifies the OBS
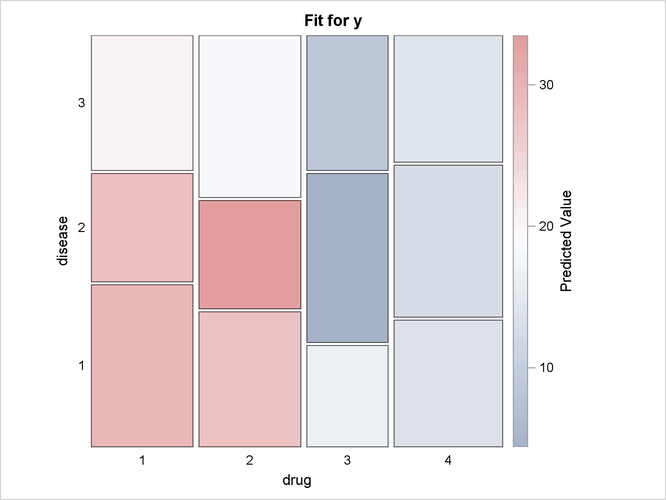
option to display the individual observations. The third EFFECTPLOT statement displays the predictions in a MOSAIC
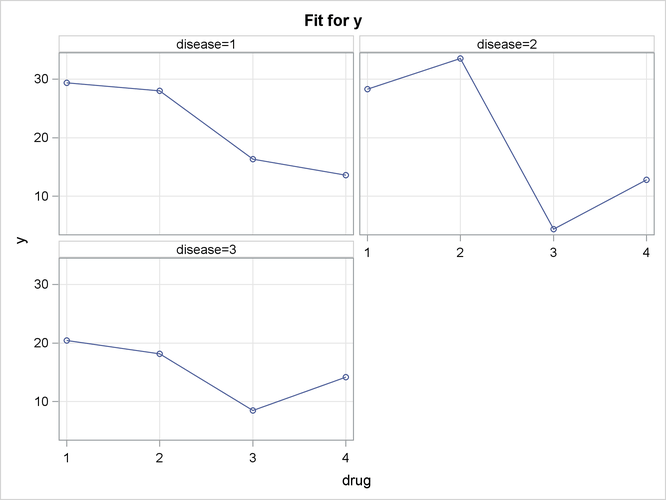
plot. The fourth EFFECTPLOT statement creates an interaction plot of predictions versus drug for each of the Disease levels and displays them in a panel.
ods graphics on; proc genmod data=a; class drug disease; model y=drug disease drug*disease / d=n; effectplot box; effectplot interaction(x=drug*disease) / obs; effectplot mosaic; effectplot interaction(plotby=disease); run; ods graphics off;
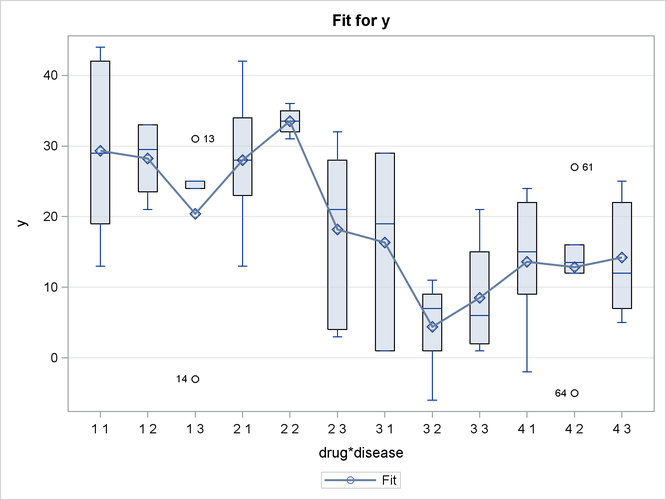
In the box plot in Output 19.2.3, the predicted values are displayed as circles; they coincide with the mean of the data at each level, all of which are displayed as diamonds. The predicted values are again connected by lines. It is difficult to draw any conclusions from this graphic.
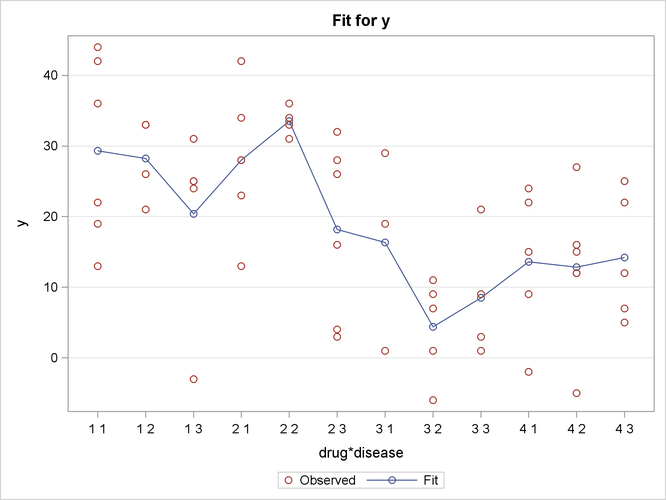
Output 19.2.4 shows the interaction plot at every combination of Drug and Disease. This plot is identical to the box plot in Output 19.2.3, except the boxes are replaced by the actual observations. Again, it is difficult to see any pattern in the plot.
Output 19.2.5 displays the mosaic plot. You can see that drugs 1 and 2 consistently outperform the other two drugs.
Output 19.2.6 groups the observations by Disease, and for each disease displays the effectiveness of the four drugs in a panel of plots.