Introduction to Regression Procedures

Introductory Example: Linear Regression

Regression analysis models the relationship between a response or outcome variable and another set of variables. This relationship is expressed through a statistical model equation that predicts a response variable (also called a dependent variable or criterion) from a function of regressor variables (also called independent variables, predictors, explanatory variables, factors, or carriers) and parameters. In a linear regression model, the predictor function is linear in the parameters (but not necessarily linear in the regressor variables). The parameters are estimated so that a measure of fit is optimized. For example, the equation for the ith observation might be

$Y_ i = \beta _0 + \beta _1 x_ i + \epsilon _ i$

where $Y_ i$ is the response variable, $x_ i$ is a regressor variable, $\beta _0$ and $\beta _1$ are unknown parameters to be estimated, and $\epsilon _ i$ is an error term. This model is called the simple linear regression (SLR) model, because it is linear in $\beta _0$ and $\beta _1$ and contains only a single regressor variable.

Suppose you are using regression analysis to relate a child’s weight to the child’s height. One application of a regression model that contains the response variable Weight is to predict a child’s weight for a known height. Suppose you collect data by measuring heights and weights of 19 randomly selected schoolchildren. A simple linear regression model that contains the response variable Weight and the regressor variable Height can be written as

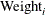
$\mr{Weight}_ i = \beta _0 + \beta _1\, \mr{Height}_ i + \epsilon _ i$

where

$\mr{Weight}_ i$: is the response variable for the ith child
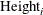
$\mr{Height}_ i$: is the regressor variable for the ith child
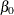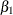
$\beta _0$ , $\beta _1$: are the unknown regression parameters
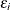
$\epsilon _ i$: is the unobservable random error associated with the ith observation

The data set Sashelp.class, which is available in the Sashelp library, identifies the children and their observed heights (the variable Height) and weights (the variable Weight). The following statements perform the regression analysis:

ods graphics on;
proc reg data=sashelp.class;
   model Weight = Height;
run;

Figure 4.1 displays the default tabular output of PROC REG for this model. Nineteen observations are read from the data set, and all observations are used in the analysis. The estimates of the two regression parameters are $\widehat{\beta }_0 = -143.02692$ and $\widehat{\beta _1} = 3.89903$ . These estimates are obtained by the least squares principle. For more information about the principle of least squares estimation and its role in linear model analysis, see the sections Classical Estimation Principles and Linear Model Theory in Chapter 3: Introduction to Statistical Modeling with SAS/STAT Software. Also see an applied regression text such as Draper and Smith (1998); Daniel and Wood (1999); Johnston and DiNardo (1997); Weisberg (2005).

Figure 4.1: Regression for Weight and Height Data

The REG Procedure

Model: MODEL1

Dependent Variable: Weight

Number of Observations Read	19
Number of Observations Used	19

Analysis of Variance
Source	DF	Sum of Squares	Mean Square	F Value	Pr > F
Model	1	7193.24912	7193.24912	57.08	<.0001
Error	17	2142.48772	126.02869
Corrected Total	18	9335.73684

Root MSE	11.22625	R-Square	0.7705
Dependent Mean	100.02632	Adj R-Sq	0.7570
Coeff Var	11.22330

Parameter Estimates
Variable	DF	Parameter Estimate	Standard Error	t Value	Pr > \|t\|
Intercept	1	-143.02692	32.27459	-4.43	0.0004
Height	1	3.89903	0.51609	7.55	<.0001

Based on the least squares estimates shown in Figure 4.1, the fitted regression line that relates height to weight is described by the equation

$\widehat{\mr{Weight}} = -143.02692 + 3.89903 \times \mr{Height}$

The "hat" notation is used to emphasize that $\widehat{\mr{Weight}}$ is not one of the original observations but a value predicted under the regression model that has been fit to the data. In the least squares solution, the following residual sum of squares is minimized and the achieved criterion value is displayed in the analysis of variance table as the error sum of squares (2142.48772):

$\mr{SSE} = \sum _{i=1}^{19} \left(\mr{Weight}_ i - \beta _0 - \beta _1 \mr{Height}_ i\right)^2$

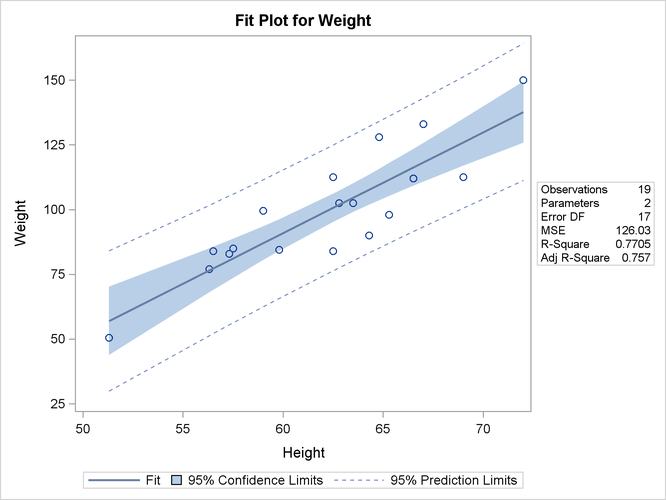
Figure 4.2 displays the fit plot that is produced by ODS Graphics. The fit plot shows the positive slope of the fitted line. The average weight of a child changes by $\widehat{\beta }_1 = 3.89903$ units for each unit change in height. The 95% confidence limits in the fit plot are pointwise limits that cover the mean weight for a particular height with probability 0.95. The prediction limits, which are wider than the confidence limits, show the pointwise limits that cover a new observation for a given height with probability 0.95.

Figure 4.2: Fit Plot for Regression of Weight on Height

Regression is often used in an exploratory fashion to look for empirical relationships, such as the relationship between Height and Weight. In this example, Height is not the cause of Weight. You would need a controlled experiment to confirm the relationship scientifically. For more information, see the section Comments on Interpreting Regression Statistics. 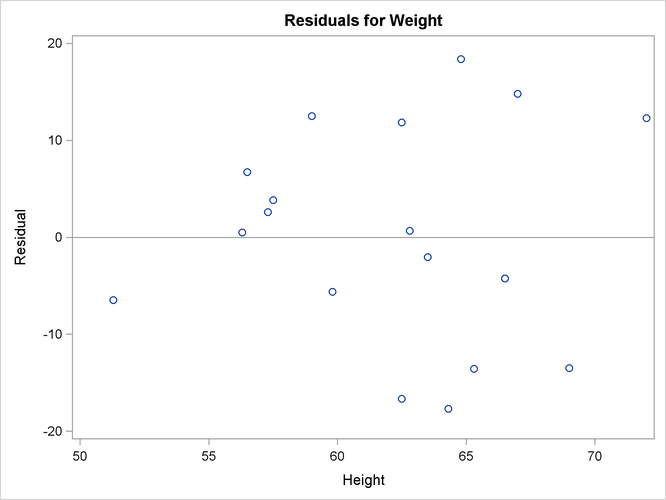A separate question from whether there is a cause-and-effect relationship between the two variables that are involved in this regression is whether the simple linear regression model adequately describes the relationship among these data. If the SLR model makes the usual assumptions about the model errors $\epsilon _ i$ , then the errors should have zero mean and equal variance and be uncorrelated. Because the children were randomly selected, the observations from different children are not correlated. If the mean function of the model is correctly specified, the fitted residuals $\mr{Weight}_ i - \widehat{\mr{Weight}}_ i$ should scatter around the zero reference line without discernible structure. The residual plot in Figure 4.3 confirms this.

Figure 4.3: Residual Plot for Regression of Weight on Height

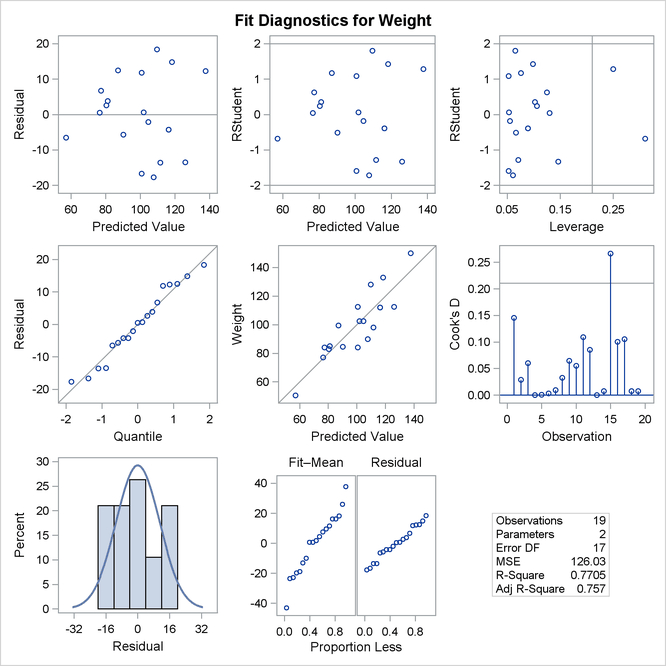
The panel of regression diagnostics in Figure 4.4 provides an even more detailed look at the model-data agreement. The graph in the upper left panel repeats the raw residual plot in Figure 4.3. The plot of the RSTUDENT residuals shows externally studentized residuals that take into account heterogeneity in the variability of the residuals. RSTUDENT residuals that exceed the threshold values of $\pm 2$ often indicate outlying observations. The residual-by-leverage plot shows that two observations have high leverage—that is, they are unusual in their height values relative to the other children. The normal-probability Q-Q plot in the second row of the panel shows that the normality assumption for the residuals is reasonable. The plot of the Cook’s D statistic shows that observation 15 exceeds the threshold value, indicating that the observation for this child has a strong influence on the regression parameter estimates.

Figure 4.4: Panel of Regression Diagnostics

For more information about the interpretation of regression diagnostics and about ODS statistical graphics with PROC REG, see Chapter 85: The REG Procedure.

SAS/STAT regression procedures produce the following information for a typical regression analysis:

parameter estimates that are derived by using the least squares criterion
estimates of the variance of the error term
estimates of the variance or standard deviation of the sampling distribution of the parameter estimates
tests of hypotheses about the parameters

SAS/STAT regression procedures can produce many other specialized diagnostic statistics, including the following:

collinearity diagnostics to measure how strongly regressors are related to other regressors and how this relationship affects the stability and variance of the estimates (REG procedure)
influence diagnostics to measure how each individual observation contributes to determining the parameter estimates, the SSE, and the fitted values (GENMOD, GLM, LOGISTIC, MIXED, NLIN, PHREG, REG, and RSREG procedures)
lack-of-fit diagnostics that measure the lack of fit of the regression model by comparing the error variance estimate to another pure error variance that does not depend on the form of the model (CATMOD, LOGISTIC, PROBIT, and RSREG procedures)
diagnostic plots that check the fit of the model (GLM, LOESS, PLS, REG, RSREG, and TPSPLINE procedures)
predicted and residual values, and confidence intervals for the mean and for an individual value (GLIMMIX, GLM, LOESS, LOGISTIC, NLIN, PLS, REG, RSREG, TPSPLINE, and TRANSREG procedures)
time series diagnostics for equally spaced time series data that measure how closely errors might be related across neighboring observations. These diagnostics can also measure functional goodness of fit for data that are sorted by regressor or response variables (REG and SAS/ETS procedures).

Many SAS/STAT procedures produce general and specialized statistical graphics through ODS Graphics to diagnose the fit of the model and the model-data agreement, and to highlight observations that strongly influence the analysis. Figure 4.2, Figure 4.3, and Figure 4.4, for example, show three of the ODS statistical graphs that are produced by PROC REG by default for the simple linear regression model. For general information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS. For specific information about the ODS statistical graphs available with a SAS/STAT procedure, see the PLOTS option in the "Syntax" section for the PROC statement and the "ODS Graphics" section in the "Details" section of the individual procedure documentation.