-
COVOUT
-
writes the parameter estimate covariance matrix to the OUTEST= data set.
-
C=rate
OPTC
-
controls how the natural response is handled. Specify the OPTC option to request that the natural response rate C be estimated. Specify the C=rate option to set the natural response rate or to provide the initial estimate of the natural response rate. The natural response
rate value must be a number between 0 and 1.
-
If you specify neither the OPTC nor the C= option, a natural response rate of zero is assumed.
-
If you specify both the OPTC and the C= option, the C= option should be a reasonable initial estimate of the natural response
rate. For example, you could use the ratio of the number of responses to the number of subjects in a control group.
-
If you specify the C= option but not the OPTC option, the natural response rate is set to the specified value and not estimated.
-
If you specify the OPTC option but not the C= option, PROC PROBIT’s action depends on the response variable, as follows:
-
If you specify either the LN or LOG10 option and some subjects have the first independent variable (dose) values less than
or equal to zero, these subjects are treated as a control group. The initial estimate of C is then the ratio of the number of responses to the number of subjects in this group.
-
If you do not specify the LN or LOG10 option or if there is no control group, then one of the following occurs:
-
If all responses are greater than zero, the initial estimate of the natural response rate is the minimal response rate (the
ratio of the number of responses to the number of subjects in a dose group) across all dose levels.
-
If one or more of the responses is zero (making the response rate zero in that dose group), the initial estimate of the natural
rate is the reciprocal of twice the largest number of subjects in any dose group in the experiment.
-
DATA=SAS-data-set
-
specifies the SAS data set to be used by PROC PROBIT. By default, the procedure uses the most recently created SAS data set.
-
GOUT=graphics-catalog
-
specifies a graphics catalog in which to save graphics output.
-
HPROB=p
-
specifies a minimum probability level for the Pearson’s chi-square to indicate a good fit. The default value is 0.10. The LACKFIT option must also be specified
for this option to have any effect. For Pearson’s goodness-of-fit chi-square values with probability greater than the HPROB=
value, the fiducial limits, if requested with the INVERSECL option, are computed by using a critical value of 1.96. For chi-square
values with probability less than the value of the HPROB= option, the critical value is a 0.95 two-sided quantile value taken
from the t distribution with degrees of freedom equal to 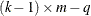 , where k is the number of levels for the response variable, m is the number of different sets of independent variable values, and q is the number of parameters fit in the model. Note that the HPROB= option can also appear in the MODEL statement.
, where k is the number of levels for the response variable, m is the number of different sets of independent variable values, and q is the number of parameters fit in the model. Note that the HPROB= option can also appear in the MODEL statement.
-
INEST=SAS-data-set
-
specifies an input SAS data set that contains initial estimates for all the parameters in the model. See the section INEST= SAS-data-set for a detailed description of the contents of the INEST= data set.
-
INVERSECL<(PROB=rates)>
-
computes confidence limits for the values of the first continuous independent variable (such as dose) that yield selected response rates. You can optionally specify a list
of response rates as rates. The response rates must be between zero and one, and can be a list separated by blanks, commas, or in the form of a DO list.
For example,
PROB = .1 TO .9 by .1
PROB = .1 .2 .3 .4
PROB = .01, .25, .75, .9
are valid lists of response rates.
If the algorithm fails to converge (this can happen when C is nonzero), missing values are reported for the confidence limits. See the section Inverse Confidence Limits for details. Note that the INVERSECL option can also appear in the MODEL statement.
-
LACKFIT
-
performs two goodness-of-fit tests (a Pearson’s chi-square test and a log-likelihood ratio chi-square test) for the fitted model.
To compute the test statistics, proper grouping of the observations into subpopulations is needed. You can use the AGGREGATE
or AGGREGATE= option for this end. See the entry for the AGGREGATE and AGGREGATE= options under the MODEL statement. If neither
AGGREGATE nor AGGREGATE= is specified, PROC PROBIT assumes each observation is from a separate subpopulation and computes
the goodness-of-fit test statistics only for the events/trials syntax.
Note: This test is not appropriate if the data are very sparse, with only a few values at each set of the independent variable
values.
If the Pearson’s chi-square test statistic is significant, then the covariance estimates and standard error estimates are
adjusted. See the section Lack-of-Fit Tests for a description of the tests. Note that the LACKFIT option can also appear in the MODEL statement.
-
LOG
LN
-
analyzes the data by replacing the first continuous independent variable with its natural logarithm. This variable is usually the level of some treatment such as dosage. In addition
to the usual output given by the INVERSECL option, the estimated dose values and 95% fiducial limits for dose are also displayed.
If you specify the OPTC option, any observations with a dose value less than or equal to zero are used in the estimation as
a control group. If you do not specify the OPTC option with the LOG or LN option, then any observations with the first continuous
independent variable values less than or equal to zero are ignored.
-
LOG10
-
specifies an analysis like that of the LN or LOG option, except that the common logarithm (log to the base 10) of the dose value is used rather than the natural logarithm.
-
NAMELEN=n
-
specifies the length of effect names in tables and output data sets to be n characters, where n is a value between 20 and 200. The default length is 20 characters.
-
NOPRINT
-
suppresses the display of all output including graphics. Note that this option temporarily disables the Output Delivery System (ODS). For more information, see Chapter 20: Using the Output Delivery System.
-
OPTC
-
controls how the natural response is handled. See the description of the C= option
on for details.
-
ORDER=DATA | FORMATTED | FREQ | INTERNAL
-
specifies the sort order for the levels of the classification variables (which are specified in the CLASS
statement).
This option applies to the levels for all classification variables, except when you use the (default) ORDER=FORMATTED option
with numeric classification variables that have no explicit format. In that case, the levels of such variables are ordered
by their internal value.
The ORDER= option can take the following values:
|
Value of ORDER=
|
Levels Sorted By
|
|
DATA
|
Order of appearance in the input data set
|
|
FORMATTED
|
External formatted value, except for numeric variables with no explicit format, which are sorted by their unformatted (internal)
value
|
|
FREQ
|
Descending frequency count; levels with the most observations come first in the order
|
|
INTERNAL
|
Unformatted value
|
By default, ORDER=FORMATTED. For ORDER=FORMATTED and ORDER=INTERNAL, the sort order is machine-dependent.
This order also applies to the levels of the response variable. Response level ordering is important because PROC PROBIT always
models the probability of response levels at the beginning of the ordering. See the section Response Level Ordering for further details.
For more information about sort order, see the chapter on the SORT procedure in the
Base SAS Procedures Guide and the discussion of BY-group processing in
SAS Language Reference: Concepts.
-
OUTEST=SAS-data-set
-
specifies a SAS data set to contain the parameter estimates and, if the COVOUT option is specified, their estimated covariances. If you omit this option, the output data set
is not created. The contents of the data set are described in the section OUTEST= SAS-data-set.
-
PLOT | PLOTS <=plot-request>
PLOT | PLOTS <=(plot-request <…plot-request > )>
-
specifies options that control details of the plots created by ODS Graphics. These plots are related to a dose variable, which is identified as the first single continuous independent variable in the
MODEL statement. If there are interaction terms with this variable in the model, the PROBIT procedure will not produce any
plot.
You can specify more than one plot request within the parentheses after PLOTS=. For a single plot request, you can omit the
parentheses.
ODS Graphics must be enabled before plots can be requested. For example:
proc probit plots=predplot;
model r/n = dose;
run;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
The following plot-requests are available.
-
ALL
-
creates all appropriate plots.
-
CDFPLOT<(LEVEL=(character-list))>
-
requests the plot of predicted cumulative distribution function (CDF) of the multinomial response variable as a function of
a single continuous independent variable (dose variable). This single continuous independent variable must be the first single
continuous independent variable listed in the MODEL statement. You can request this plot only with a multinomial model.
The LEVEL= suboption specifies the levels of the multinomial response variable for which the CDF curves are requested. There
are k – 1 curves for a k-level multinomial response variable (for the highest level, it is the constant line 1). You can specify any of them to be
plotted by the LEVEL= suboption.
-
IPPPLOT
-
requests the inverse plot of the predicted probability against the first single continuous variable (dose variable) in the
MODEL statement for the binomial model. You can request this plot only with a binomial model. The confidence limits for the
predicted values of the dose variable are the computed fiducial limits, not the inverse of the confidence limits of the predicted
probabilities. See the section Inverse Confidence Limits for more details.
-
LPREDPLOT<(LEVEL=(character-list))>
-
requests the plot of the linear predictor 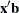 against the first single continuous variable (dose variable) in the MODEL statement for either the binomial model or the
multinomial model. The confidence limits for the predicted values are available only for the binomial model.
against the first single continuous variable (dose variable) in the MODEL statement for either the binomial model or the
multinomial model. The confidence limits for the predicted values are available only for the binomial model.
For the multinomial model, you can use the LEVEL= suboption to specify the levels for which the linear predictor lines are
plotted.
-
NONE
-
suppresses all plots.
-
PREDPPLOT<(LEVEL=(character-list))>
-
requests the plot of the predicted probability against the first single continuous variable (dose variable) in the MODEL statement
for both the binomial model and the multinomial model. Confidence limits are available only for the binomial model.
For the multinomial model, you can use the LEVEL= suboption to specify the levels for which the linear predictor lines are
plotted.
-
XDATA=SAS-data-set
-
specifies an input SAS data set that contains values for all the independent variables in the MODEL statement and variables in the CLASS statement. If there are covariates specified in a
MODEL statement, you specify fixed values for the effects in the MODEL statement by the XDATA= data set when predicted values
and/or fiducial limits for a single continuous variable (dose variable) are required. These specified values for the effects
in the MODEL statement are also used for generating plots. See the section XDATA= SAS-data-set for a detailed description of the contents of the XDATA= data set.

 PROC PROBIT StatementBY StatementCDFPLOT StatementCLASS StatementEFFECTPLOT StatementESTIMATE StatementINSET StatementIPPPLOT StatementLPREDPLOT StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementPREDPPLOT StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PROBIT StatementBY StatementCDFPLOT StatementCLASS StatementEFFECTPLOT StatementESTIMATE StatementINSET StatementIPPPLOT StatementLPREDPLOT StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementPREDPPLOT StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement Missing ValuesResponse Level OrderingComputational MethodDistributionsINEST= SAS-data-setModel SpecificationLack-of-Fit TestsRescaling the Covariance MatrixTolerance DistributionInverse Confidence LimitsOUTEST= SAS-data-setXDATA= SAS-data-setTraditional High-Resolution GraphicsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingComputational MethodDistributionsINEST= SAS-data-setModel SpecificationLack-of-Fit TestsRescaling the Covariance MatrixTolerance DistributionInverse Confidence LimitsOUTEST= SAS-data-setXDATA= SAS-data-setTraditional High-Resolution GraphicsDisplayed OutputODS Table NamesODS Graphics