-
ANGLE=angle | (angle1, …, anglek)
-
specifies the angle of the major axis for anisotropic models, measured in degrees clockwise from the N–S axis. The default is ANGLE=0.
In the case of a nested semivariogram model with k nestings, you have the following two ways to specify the anisotropy major axis: you can specify only one angle which is then applied to all nested forms, or you can specify one angle for each of the k nestings.
Note: The syntax makes it possible to specify different angles for different forms of the nested model, but this practice is rarely
used.
-
FORM=form | (form1, …, formk)
-
specifies the functional form (type) of the semivariogram model. Use the syntax with the single form to specify a non-nested model. Use the syntax with forms formi, 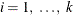 , to specify a nested model with k structures. Each of the forms can be any of the following:
, to specify a nested model with k structures. Each of the forms can be any of the following:
-
CUBIC | EXPONENTIAL | GAUSSIAN | MATERN |
PENTASPHERICAL | SINEHOLEEFFECT | SPHERICAL
CUB | EXP | GAU | MAT | PEN | SHE | SPH
-
specify the functional form (type).
For example, the syntax
FORM=GAU
specifies a model with a single Gaussian structure. Also, the syntax
FORM=(EXP,SHE,MAT)
specifies a nested model with an exponential, a sine hole effect, and a Matérn structure. Finally
FORM=(EXP,EXP)
specifies a nested model with two structures both of which are exponential.
Note: In the documentation, models are named either by using their full names or by using the first three letters of their structures.
Also, the names of different structures in a nested model are separated by a hyphen (-). According to this convention, the
previous examples illustrate how to specify a GAU, an EXP-SHE-MAT, and an EXP-EXP model, respectively, with the FORM= option.
All the supported model forms have two parameters specified by the SCALE=
and RANGE=
options, except for the MATERN model which has a third parameter specified by the SMOOTH=
option. A FORM= value is required, unless you specify the MDATA=
option or the STORESELECT
option.
Computation of the MATERN covariance is numerically demanding. As a result, simulations that use Matérn covariance structures
can be time-consuming.
-
MDATA=SAS-data-set
-
specifies the input data set that contains parameter values for the covariance or semivariogram model. The MDATA= option cannot be combined with any of the FORM=
or STORESELECT
options.
The MDATA= data set must contain variables named SCALE, RANGE, and FORM, and it can optionally contain variables NUGGET, ANGLE, and RATIO. If you specify the MATERN form, then you must also include a variable named SMOOTH in the MDATA= data set.
The FORM variable must be a character variable, and it can assume only the values allowed in the explicit FORM=
syntax described previously. The RANGE, SCALE and SMOOTH variables must be numeric. The optional variables ANGLE, RATIO, and NUGGET must also be numeric if present.
The number of observations present in the MDATA=
data set corresponds to the level of nesting of the covariance or semivariogram model. For example, to specify a non-nested
model that uses a spherical covariance, an MDATA=
data set might contain the following statements:
data md1;
input scale range form $;
datalines;
25 10 SPH
;
The PROC SIM2D statement to use the MDATA=
specification is of the form shown in the following:
proc sim2d data=...;
sim var=.... mdata=md1;
run;
This is equivalent to the following explicit specification of the covariance model parameters:
proc sim2d data=...;
sim var=.... scale=25 range=10 form=sph;
run;
The following MDATA=
data set is an example of an anisotropic nested model:
data md2;
input scale range form $ nugget angle ratio smooth;
datalines;
20 8 SPH 5 35 .7 .
12 3 MAT 5 0 .8 2.8
4 1 GAU 5 45 .5 .
;
proc sim2d data=...;
sim var=.... mdata=md2;
run;
This is equivalent to the following explicit specification of the covariance model parameters:
proc sim2d data=...;
sim var=.... scale=(20,12,4) range=(8,3,1) form=(SPH,MAT,GAU)
angle=(35,0,45) ratio=(.7,.8,.5) nugget=5 smooth=2.8;
run;
This example is somewhat artificial in that it is usually hard to detect different anisotropy directions and ratios for different
nestings by using an experimental semivariogram.
Note: The NUGGET variable value is the same for all nestings. This is always the case; the nugget effect is a single additive term for all
models. For further details, see the section The Nugget Effect in Chapter 55: The KRIGE2D Procedure.
The example also shows that if you specify a MATERN form in the nested model, then the SMOOTH variable must be specified for all nestings in the MDATA= data set. You simply specify the SMOOTH value as missing for nestings other than MATERN.
The SIMULATE
statement can be given a label. This is useful for identification in the OUTSIM=
data set when multiple SIMULATE
statements are specified. For example:
proc sim2d data=...;
gauss1: sim var=.... form=gau;
mean ....;
gauss2: sim var=.... form gau;
mean ....;
exp1: sim var=.... form=exp;
mean ....;
exp2: sim var=.... form=exp;
mean ....;
run;
In the OUTSIM=
data set, the values "GAUSS1," "GAUSS2," "EXP1," and "EXP2" for the LABEL variable help to identify the realizations that correspond to the four SIMULATE
statements. If you do not provide a label for a SIMULATE
statement, a default label of SIMn is given, where n is the number of unlabeled SIMULATE
statements seen so far.
-
NUGGET=number
-
specifies the nugget effect for the model. This effect is due to a discontinuity in the semivariogram as determined by plotting the sample semivariogram (see the section
The Nugget Effect in Chapter 55: The KRIGE2D Procedure, for details). For models without any nugget effect, the NUGGET= option is left out. The default is NUGGET=0.
-
RANGE=range | (range1, …, rangek)
-
specifies the range parameter in the semivariogram models. In the case of a nested semivariogram model with k nestings, you must specify a range for each nesting.
The range parameter is the divisor in the exponent in all supported models. It has the units of distance or distance squared
for these models, and it is related to the correlation scale for the underlying spatial process.
See the section Theoretical Semivariogram Models in Chapter 55: The KRIGE2D Procedure, for details about how the RANGE= values are determined.
-
RATIO=ratio | (ratio1, …, ratiok)
-
specifies the ratio of the length of the minor axis to the length of the major axis for anisotropic models. The value of the RATIO= option must be between 0 and 1. In the
case of a nested semivariogram model with k nestings, you can specify a ratio for each nesting. The default is RATIO=1.
-
SCALE=scale | (scale1, …, scalek)
-
specifies the scale (or sill) parameter in semivariogram models. In the case of a nested semivariogram model with k nestings, you must specify a scale for each nesting. The scale parameter is the multiplicative factor in all supported models;
it has the same units as the variance of the VAR=
variable.
See the section Theoretical Semivariogram Models in Chapter 55: The KRIGE2D Procedure, for details about how the SCALE= values are determined.
-
SEED=seed-value
-
specifies the seed to use for the random number generator. The SEED= option seed-value has to be an integer.
-
SINGULAR=number
-
gives the singularity criterion for solving the set of linear equations involved in the computation of the mean and covariance of the conditional distribution associated
with a given SIMULATE
statement. The larger the value of the SINGULAR= option, the easier it is for the covariance matrix system to be declared
singular. The default is SINGULAR=1E–8.
For more details about the use of the SINGULAR= option, see the section Computational and Theoretical Details of Spatial Simulation.
-
SMOOTH=smooth | (smooth1, …, smoothm)
-
specifies the smoothness parameter 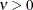 in the Matérn type of semivariance structures. The special case
in the Matérn type of semivariance structures. The special case 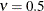 is equivalent to the exponential model, whereas
is equivalent to the exponential model, whereas 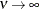 gives the Gaussian model.
gives the Gaussian model.
When you specify m different MATERN forms in the FORM=
option, you must also provide m smoothness values in the SMOOTH option. If you must specify more than one smoothness value, the values are assigned sequentially
to the MATERN nestings in the order the nestings are specified. If you specify more smoothness values than necessary, then
values in excess are ignored.
-
STORESELECT(ssel-options)
SSEL(ssel-options)
-
specifies that information from an input item store be used for the prediction. You cannot combine the STORESELECT option with any of the FORM=
or MDATA=
options. The STORESELECT option has the following ssel-options:
-
TYPE=field-type
-
specifies whether to perform isotropic or anisotropic simulation. You can choose the field-type from one of the following:
-
ISO
-
specifies isotropic field for the simulation.
-
ANIGEO | GEO
-
specifies a field with geometric anisotropy for the simulation.
-
ANIZON(zonal-form1, …, zonal-formn)
ZON(zonal-form1, …, zonal-formn)
-
specifies a field with zonal anisotropy for the simulation. Each zonal-formi, 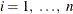 , can be any of the following:
, can be any of the following:
-
CUB | EXP | GAU | MAT | PEN | SHE | SPH
-
specify a form for the simulation.
Each zonal-formi, 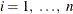 , is a structure in the purely zonal component of the correlation model in the direction angle of the minor anisotropy axis.
For this reason, when you specify the TYPE=ANIZON suboption you must also specify the nonzonal component of the correlation
model in the MODEL=
suboption of the STORESELECT option. Assume the nonzonal component has k structures; these are common across all directions and each one has the same scale in all directions. In that sense, you
use the TYPE=ANIZON suboption to specify only the n zonal anisotropy structures of an input store (
, is a structure in the purely zonal component of the correlation model in the direction angle of the minor anisotropy axis.
For this reason, when you specify the TYPE=ANIZON suboption you must also specify the nonzonal component of the correlation
model in the MODEL=
suboption of the STORESELECT option. Assume the nonzonal component has k structures; these are common across all directions and each one has the same scale in all directions. In that sense, you
use the TYPE=ANIZON suboption to specify only the n zonal anisotropy structures of an input store (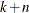 )-structure nested model in the direction angle of the minor anisotropy axis.
)-structure nested model in the direction angle of the minor anisotropy axis.
Given this specification, 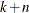 must be up to the maximum number of nested model structures that is supported by the item store. See also the MODEL=
suboption of the STORESELECT option.
must be up to the maximum number of nested model structures that is supported by the item store. See also the MODEL=
suboption of the STORESELECT option.
In conclusion, you can use an input item store for prediction with zonal anisotropy if you know that every structure in the
nonzonal model component has the same scale across all directions. When this condition does not apply for the item store models,
specify the model parameters explicitly in the SIMULATE
statement.
Computation of the MATERN covariance is numerically demanding. As a result, predictions that use Matérn covariance structures
can be time-consuming.
If you omit the TYPE= option, the default behavior is TYPE=ISO when the input item store contains information for only one
angle or for the omnidirectional case. If you specify an item store with information for more than one direction, then the
default behavior is TYPE=ANIGEO.
When you specify TYPE=ISO to request isotropic analysis in the presence of an item store with information for multiple directions,
you must specify the ANGLEID=
suboption of the STORESELECT option with one argument. This argument specifies which of the direction angles information
to use for the isotropic analysis.
When you indicate the presence of anisotropy with the TYPE=ANIGEO or TYPE=ANIZON suboptions of the STORESELECT option, the
following conditions apply:
-
You must specify the ANGLEID=
suboption of the STORESELECT option to designate the major and minor anisotropy axes. See the ANGLEID=
suboption of the STORESELECT option for details.
-
-
For TYPE=ANIGEO, ensure that you have the same scale in all anisotropy directions.
-
For TYPE=ANIZON, ensure that the nonzonal component scale is the same in all anisotropy directions.
If you import a nested model, these rules also apply to each one of the nested structures.
-
Model ranges in the major anisotropy axis must be longer than ranges in the minor anisotropy axis.
-
Any Matérn covariance structure must maintain its smoothness parameter value in all anisotropy directions.
-
ANGLEID=angleid1 | (angleid1, angleid2)
-
specifies which direction angles in the input item store be used for simulation. The angles are identified by the corresponding number in the AngleID column of the "Store Models Information" table, or by the AngleID parameter in the table title when you specify the INFO
(DETAILS
) option in the RESTORE
statement.
If you request isotropic prediction in the TYPE=
suboption of the STORESELECT option and the item store has omnidirectional contents or information about only one angle,
then the ANGLEID= option is ignored. The simulation input comes from the omnidirectional information. In the case of a single
angle, you still perform isotropic simulation and the model parameters are provided by the model in the single direction angle
in the item store. However, if the item store contains information for more than one angle, then you must specify one angle
ID in angleid1. The model information from the corresponding angle is then used in your isotropic simulation.
When you specify an anisotropic simulation in the TYPE=
option of the STORESELECT option, you need to have information about two perpendicular direction angles. One of them is the
major and the other is the minor anisotropy axis. You must always specify the major anisotropy axis angle ID in angleid1 and the minor anisotropy axis angle ID in angleid2. This means that the range parameters of the model forms in the angle designated by the angleid1 need to be larger than the corresponding ranges of the forms in the angle designated by the angleid2. Conveniently, if the item store has only two angles, then you only need to specify the ID angleid1 of the major anisotropy axis angle. If the item store has only one angle, then you cannot perform anisotropic simulation
with input from the item store.
Note: You can perform geometric anisotropic analysis even if the item store does not contain information about a direction that
is perpendicular to the one specified by angleid1. This is possible due to the geometry of the ellipse. In particular, when you specify the major axis with angleid1 and an angle ID for a second direction with a corresponding smaller range, then PROC SIM2D automatically computes the minor
anisotropy axis range and the necessary range ratio parameter.
Anisotropic analysis is not possible when you specify instances of the same angle in the input item store. It is possible
that PROC VARIOGRAM produces an item store where two or more directions can be the same if their corresponding correlation
models were obtained for different angle tolerances or bandwidths in the VARIOGRAM procedure. Consequently, you cannot specify
anisotropic simulation if the input store contains only two angles that are the same or if you specify angleid1 and angleid2 that correspond to equal angles.
-
MODEL=form | (form1, …, formk)
-
specifies the theoretical semivariogram model selection to use for the simulation. Use any combination of one, two, or three forms to describe a model in the input item store because up to
three nested structures are supported. Each formi, 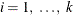 , can be any of the following:
, can be any of the following:
-
CUB | EXP | GAU | MAT | PEN | SHE | SPH
-
specify the selection model.
Computation of the MATERN covariance is numerically demanding. As a result, simulations that use Matérn covariance structures
can be time-consuming.
All fitted models that are stored in the input item store contain information about their component parameters and also about
the nugget effect if any. The SIM2D procedure retrieves this information when you make a model selection in the MODEL= option,
and you do not need to individually specify a nugget effect or any other parameter of the model.
By default, the model that is ranked first among the models for a given angle in the item store is used for the simulation
task. If more than one model is available in the item store, then you can specify the MODEL= option to use a different model
for the simulation.
In an anisotropic simulation, the default selection is the model that is ranked first in the direction angle of the major
anisotropy axis. If you specify the TYPE=
ANIGEO option, then a model that consists of identical structures needs to be present in the selected minor anisotropy axis
angle in the item store. If you specify the TYPE=
ANIZON option, then a model with the exact same first k structures must be present in the selected minor anisotropy axis angle, and it must feature at least one more structure as
a zonal component. The zonal component is specified separately in the TYPE=
ANIZON suboption of the STORESELECT option. Consequently, remember that in zonal anisotropy the MODEL= suboption designates
only the nonzonal component of the correlation model in the minor anisotropy axis direction. In all, if there are k common structures and n structures in the purely zonal component, then 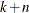 must be up to the maximum number of nested model structures that is supported by the item store.
must be up to the maximum number of nested model structures that is supported by the item store.
-
SVAR=store-var | (store-varlist)
-
specifies one store-var item store variable or a list store-varlist of variables that are present in the item store. This option selects one or more item store variables whose correlation models
you want to use in the current simulation task.
If you are performing a conditional simulation, then PROC SIM2D searches the input item store for the variable that is specified
in the VAR=
option of the SIMULATE
statement. Then, the procedure selects the appropriate correlation model for the task. In this case, if you specify the SVAR=
option, it is ignored. However, when you request an unconditional simulation and specify input from an item store, then you
must also use SVAR= to specify a source for your correlation model.
In comparison to the other two ways of specifying a correlation model in PROC SIM2D, the STORESELECT option is quite different
because you can avoid explicit specification of all parameter values of a model. When you specify the STORESELECT option,
then the corresponding scale, range, nugget effect, and smoothness (if appropriate) parameter values are invoked as saved
attributes of the model that you select from the item store.
In the case of anisotropy, you specify the angles indirectly with the ANGLEID=
option of the STORESELECT option, and the ratios are computed implicitly by using the selected model ranges. Explore how
to specify valid anisotropical models imported from an input item store with the two examples that follow.
In the first example, assume the input item store InStoreGeo contains exponential models in the angles 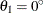 ,
, 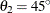 , and
, and 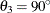 . You know in advance that all models have the same scale
. You know in advance that all models have the same scale 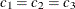 across these directions and that the respective ranges are
across these directions and that the respective ranges are 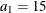 ,
, 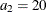 , and
, and 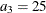 in distance units. Hence, you have a case of geometric anisotropy where the major anisotropy axis is in the direction of
angle
in distance units. Hence, you have a case of geometric anisotropy where the major anisotropy axis is in the direction of
angle 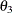 and the minor anisotropy axis is in the direction of angle
and the minor anisotropy axis is in the direction of angle 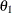 . The following statements in PROC SIM2D use the information in the item store
. The following statements in PROC SIM2D use the information in the item store InStoreGeo to perform simulation under the assumption of geometric anisotropy:
proc sim2d data=...;
restore in=InStoreGeo;
simulate storeselect(model=exp type=anigeo angleid=(3,1));
run;
For the second example, assume a case of zonal anisotropy. Consider the input item store InStoreZon, which contains models in the two angles, 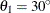 and
and 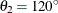 . Specifically, in
. Specifically, in 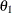 you have an exponential-spherical model: the exponential structure has scale
you have an exponential-spherical model: the exponential structure has scale 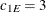 and range
and range 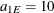 ; the spherical structure has scale
; the spherical structure has scale 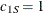 and range
and range 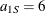 . In direction
. In direction 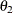 you have an exponential model with scale
you have an exponential model with scale 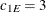 and range
and range 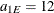 . Hence, the zonal anisotropy major axis is in the direction of the lowest total variance, which is in angle
. Hence, the zonal anisotropy major axis is in the direction of the lowest total variance, which is in angle 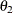 ; then, the minor axis is in the direction of angle
; then, the minor axis is in the direction of angle 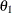 . The following statements in PROC SIM2D use the information in the store
. The following statements in PROC SIM2D use the information in the store InStoreZon to perform simulation under the assumption of zonal anisotropy:
proc sim2d data=...;
restore in=InStoreZon;
simulate storeselect(model=exp type=anizon(sph) angleid=(2,1));
run;
