The SURVEYREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC SURVEYREG StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement
PROC SURVEYREG StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement -
Details

-
Examples

- References
You can use PROC SURVEYREG to perform domain analysis in a subgroup of your interest. To illustrate, this example uses a data set from the National Health and Nutrition Examination Survey I (NHANES I) Epidemiologic Followup Study (NHEFS), described in Example 100.2 in Chapter 100: The SURVEYPHREG Procedure.
The NHEFS is a national longitudinal survey that is conducted by the National Center for Health Statistics, the National Institute on Aging, and some other agencies of the Public Health Service in the United States. Some important objectives of this survey are to determine the relationships between clinical, nutritional, and behavioral factors; to determine the relationship between mortality and hospital utilization; and to monitor changes in risk factors for the initial cohort that represents the NHANES I population. A cohort of size 14,407, which includes all persons 25 to 74 years old who completed a medical examination at NHANES I in 1971–1975, was selected for the NHEFS. Personal interviews were conducted for every selected unit during the first wave of data collection from the year 1982 to 1984. Follow-up studies were conducted in 1986, 1987, and 1992. In the year 1986, only nondeceased persons 55 to 74 years old (as reported in the base year survey) were interviewed. The 1987 and 1992 NHEFS contain the entire nondeceased NHEFS cohort. Vital and tracing status data, interview data, health care facility stay data, and mortality data for all four waves are available for public use. See http://www.cdc.gov/nchs/nhanes/nhefs/nhefs.htm for more information about the survey and the data sets.
For illustration purposes, 1,018 observations from the 1987 NHEFS public use interview data are used to create the data set
cancer. The observations are obtained from 10 strata that contain 596 PSUs. The sum of observation weights for these selected units
is over 19 million. Observation weights range from 359 to 129,359 with a mean of 18,747.69 and a median of 11,414.
The following variables are used in this example:
-
ObsNo, unit identification -
Strata, stratum identification -
PSU, identification for primary sampling units -
ObservationWt, sampling weight associated with each unit -
Age, the event-time variable, defined as follows:-
age of the subject when the first cancer was reported for subjects with reported cancer
-
age of the subject at death for deceased subjects without reported cancer
-
age of the subject as reported in 1987 follow-up (this value is used for nondeceased subjects who never reported cancer)
-
age of the subject for the entry year 1971–1975 survey if the subject has cancer (or is deceased) but the date of incident is not reported
-
-
Cancer, cancer indicator (1 = cancer reported, 0 = cancer not reported) -
BodyWeight, body weight of the subject as reported in the 1987 follow-up, or an imputed body weight based on the subject’s age in the entry year 1971–1975 survey
The following SAS statements create the data set cancer. Note that BodyWeight for a few observations (8%) is imputed based on Age by using a deterministic regression imputation model (Särndal and Lundström (2005, chapter 12)). The imputed values are treated as observed values in this example. In other words, this example treats the
data set Cancer as the observed data set.
data cancer; input ObsNo Strata PSU ObservationWt Age Cancer BodyWeight; datalines; 1 3 002 3805 53 1 175 2 3 002 6107 77 0 175 3 3 039 2968 50 0 160 4 3 084 30438 52 0 145 5 3 007 5081 80 0 127 6 3 009 3891 62 0 180 7 3 009 3580 50 0 157 8 3 022 2968 56 0 142 9 3 050 23748 60 0 140 10 3 060 48264 69 0 168 ... more lines ... 1016 4 002 2689 40 0 120 1017 4 092 45888 52 0 166 1018 4 035 4347 58 0 156 ;
Suppose you want to study how aging affects body weight in the subgroup of cancer patients for the base year survey population. Because whether an individual has cancer or not is unrelated to the design of the sample, this kind of analysis is called domain analysis (subgroup analysis).
The following statements request a linear regression of BodyWeight on Age among cancer patients. The STRATA, CLUSTER, and WEIGHT statements identify the variance strata, PSUs, and analysis weights,
respectively. The DOMAIN statement defines the subgroups of people who have been diagnosed with cancer and people who do not
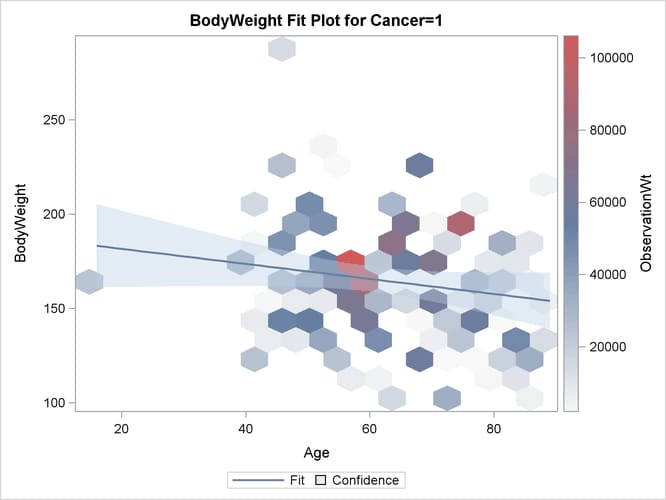
have cancer. The ODS SELECT statement requests that PROC SURVEYREG display only the analysis in the subgroup Cancer = 1 in the output. The PLOT= option in the PROC statement requests that weights be represented as a heat map with hexagonal
bins.
title1 'Study of Body Weight and Age among Cancer Patients'; ods graphics on; proc surveyreg data=cancer plot=fit(weight=heatmap shape=hex); strata strata; cluster psu; weight ObservationWt; model bodyweight = age; domain cancer; ods select where=(_labelpath_ ? 'Cancer=1'); run; ods graphics off;
Output 101.7.1 gives a summary of the data and the parameter estimates of the linear regression in domain Cancer = 1. The analysis indicates that aging does not significantly affect body weight among cancer patients.
Output 101.7.1: Domain Analysis Among Cancer Patients
| Study of Body Weight and Age among Cancer Patients |
| Domain Summary | |
|---|---|
| Number of Observations | 1017 |
| Number of Observations in Domain | 119 |
| Number of Observations Not in Domain | 898 |
| Sum of Weights in Domain | 2211545.0 |
| Weighted Mean of BodyWeight | 164.87655 |
| Weighted Sum of BodyWeight | 364631909 |
When ODS Graphics is enabled and the model contains a single continuous regressor, PROC SURVEYREG displays a plot of the model fitting, which is shown in Output 101.7.2.