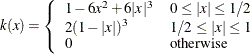The PANEL Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR SquareSpecification TestsPanel Data Poolability TestPanel Data Unit Root TestsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names
Missing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR SquareSpecification TestsPanel Data Poolability TestPanel Data Unit Root TestsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names -
Example

- References
Heteroscedasticity- and Autocorrelation-Consistent Covariance Matrices
The HAC option in the MODEL statement selects the type of heteroscedasticity- and autocorrelation-consistent covariance matrix.
As with the HCCME option, an estimator of the middle expression ![]() in sandwich form is needed. With the HAC option, it is estimated as
in sandwich form is needed. With the HAC option, it is estimated as
|
|
, where ![]() is the real-valued kernel function[2],
is the real-valued kernel function[2], ![]() is the bandwidth parameter, and
is the bandwidth parameter, and ![]() is the adjustment factor of small sample degrees of freedom (that is,
is the adjustment factor of small sample degrees of freedom (that is, ![]() if the ADJUSTDF option is not specified and otherwise
if the ADJUSTDF option is not specified and otherwise ![]() , where
, where ![]() is the number of parameters including dummy variables). The types of kernel functions are listed in Table 20.1.
is the number of parameters including dummy variables). The types of kernel functions are listed in Table 20.1.
Table 20.1: Kernel Functions
|
Kernel Name |
Equation |
|---|---|
|
Bartlett |
|
|
Parzen |
|
|
Quadratic spectral |
|
|
Truncated |
|
|
Tukey-Hanning |
|
When the BANDWIDTH=ANDREWS option is specified, the bandwidth parameter is estimated as shown in Table 20.2.
Table 20.2: Bandwidth Parameter Estimation
|
Kernel Name |
Bandwidth Parameter |
|---|---|
|
Bartlett |
|
|
Parzen |
|
|
Quadratic spectral |
|
|
Truncated |
|
|
Tukey-Hanning |
|
Let ![]() denote each series in
denote each series in ![]() , and let
, and let ![]() denote the corresponding estimates of the autoregressive and innovation variance parameters of the AR(1) model on
denote the corresponding estimates of the autoregressive and innovation variance parameters of the AR(1) model on ![]() ,
, ![]() , where the AR(1) model is parameterized as
, where the AR(1) model is parameterized as ![]() with
with ![]() . The
. The ![]() and
and ![]() are estimated with the following formulas:
are estimated with the following formulas:
![\[ \alpha (1) = \frac{\sum _{a=1}^ k{\frac{4\rho _ a^{2}\sigma _ a^4}{(1-\rho _ a)^6(1+\rho _ a)^2}}}{\sum _{a=1}^ k{\frac{\sigma _ a^4}{(1-\rho _ a)^4}}} \\ \alpha (2) = \frac{\sum _{a=1}^ k{\frac{4\rho _ a^{2}\sigma _ a^4}{(1-\rho _ a)^8}}}{\sum _{a=1}^ k{\frac{\sigma _ a^4}{(1-\rho _ a)^4}}} \]](images/etsug_panel0735.png) |
When you specify BANDWIDTH=NEWEYWEST94, according to Newey and West(1994) the bandwidth parameter is estimated as shown in Table 20.3.
Table 20.3: Bandwidth Parameter Estimation
|
Kernel Name |
Bandwidth Parameter |
|---|---|
|
Bartlett |
|
|
Parzen |
|
|
Quadratic spectral |
|
|
Truncated |
|
|
Tukey-Hanning |
|
The ![]() and
and ![]() are estimated with the following formulas:
are estimated with the following formulas:
|
|
where ![]() is the lag selection parameter and is determined by kernels, as listed in Table 20.4.
is the lag selection parameter and is determined by kernels, as listed in Table 20.4.
Table 20.4: Lag Selection Parameter Estimation
|
Kernel Name |
Lag Selection Parameter |
|---|---|
|
Bartlett |
|
|
Parzen |
|
|
Quadratic Spectral |
|
|
Truncated |
|
|
Tukey-Hanning |
|
The ![]() in Table 20.4 is specified by the C= option; by default, C=12.
in Table 20.4 is specified by the C= option; by default, C=12.
The ![]() is estimated with the equation
is estimated with the equation
|
|
where ![]() is the same as in the Andrews method and
is the same as in the Andrews method and ![]() is 1 if the NOINT option in the MODEL statement is specified, and 2 otherwise.
is 1 if the NOINT option in the MODEL statement is specified, and 2 otherwise.
When you specify BANDWIDTH=SAMPLESIZE, the bandwidth parameter is estimated with the equation
|
|
where ![]() is the sample size,
is the sample size, ![]() is the largest integer less than or equal to
is the largest integer less than or equal to ![]() , and
, and ![]() ,
, ![]() , and
, and ![]() are values specified by BANDWIDTH=SAMPLESIZE(GAMMA=, RATE=, CONSTANT=) options, respectively.
are values specified by BANDWIDTH=SAMPLESIZE(GAMMA=, RATE=, CONSTANT=) options, respectively.
If the PREWHITENING option is specified in the MODEL statement, ![]() is prewhitened by the VAR(1) model,
is prewhitened by the VAR(1) model,
|
|
Then ![]() is calculated by
is calculated by
|
|