Normal Copula :: SAS/ETS(R) 13.1 User's Guide

Normal Copula

Subsections:

Simulation
Fitting

Let $u_ j \sim U(0,1)$ for $j=1,\ldots ,m$ , where $U(0,1)$ represents the uniform distribution on the $[0,1]$ interval. Let $\Sigma$ be the correlation matrix with $m(m-1)/2$ parameters satisfying the positive semidefiniteness constraint. The normal copula can be written as

$\begin{equation*} C_{\Sigma }(u_1, u_2,{\ldots } u_ m) = \bm {\Phi }_\Sigma \Bigl (\Phi ^{-1} (u_1),{\ldots } \Phi ^{-1} (u_ m)\Bigr ) \end{equation*}$

where $\Phi$ is the distribution function of a standard normal random variable and $\bm {\Phi }_\Sigma$ is the $m$ -variate standard normal distribution with mean vector $0$ and covariance matrix $\Sigma$ . That is, the distribution $\bm {\Phi }_\Sigma$ is $N_ m(0,\Sigma )$ .

Simulation

For the normal copula, the input of the simulation is the correlation matrix $\Sigma$ . The normal copula can be simulated by the following steps in which $\bm U= (U_1,\ldots ,U_ m)$ denotes one random draw from the copula:

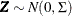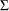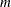Generate a multivariate normal vector $\bm Z \sim N(0,\Sigma )$ where $\Sigma$ is an $m$ -dimensional correlation matrix.
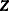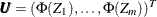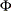Transform the vector $\bm Z$ into $\bm U= (\Phi (Z_1),\ldots ,\Phi (Z_ m))^ T$ , where $\Phi$ is the distribution function of univariate standard normal.

The first step can be achieved by Cholesky decomposition of the correlation matrix $\Sigma =LL^ T$ where $L$ is a lower triangular matrix with positive elements on the diagonal. If $\bm {\tilde{Z}} \sim N(0,I)$ , then $L\bm {\tilde{Z}} \sim N(0,\Sigma )$ .

Fitting

To fit a normal copula is to estimate the covariance matrix $\Sigma$ from an input sample data set. Given a random sample $\bm u_ i = (u_{i,1},\ldots ,u_{i,m})^\top$ where $i=1,\ldots ,n$ , the log-likelihood function is

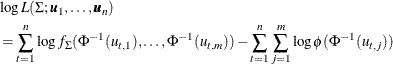
$\begin{align*} & \log L(\Sigma ;\bm u_1,\ldots , \bm u_ n)\\ & =\sum _{t=1}^ n \log f_\Sigma (\Phi ^{-1}(u_{t,1}),\ldots ,\Phi ^{-1}(u_{t,m})) -\sum _{t=1}^ n \sum _{j=1}^ m \log \phi (\Phi ^{-1}(u_{t,j})) \end{align*}$

Here $f_\Sigma$ is the joint density of the multivariate normal with mean zero and variance $\Sigma$ , and $\phi$ is the univariate density of the standard normal distribution. Note that the second term is not related to the parameters $\Sigma$ and, therefore, can be ignored during the optimization. The restriction that $\Sigma$ is a correlation matrix is very inconvenient, and it is common practice to circumvent this problem by first assuming that $\Sigma$ has the covariance form. Therefore, $\Sigma$ can be estimated by

$\widehat{\Sigma } = \frac{1}{n} \sum _{i=1}^{n} \bm {\zeta }_ i \bm {\zeta }_ i^ T$

where

$\bm {\zeta }_ i = \bigl (\Phi ^{-1}(u_{i,1}),\Phi ^{-1}(u_{i,2}),{\ldots },\Phi ^{-1}(u_{i,m})\bigr )^ T$

This estimate is consistent with the form of a covariance matrix but not necessarily with the form of a correlation matrix. The approximation to the original MLE problem can be obtained using the normalizing operator defined as follows:

$\begin{align*} \Delta (\Sigma ) & = \textrm{diag}(\sigma _{11}^{1/2},\ldots ,\sigma _{mm}^{1/2})\\ \mathcal{P}(\Sigma )& = (\Delta (\Sigma ))^{-1} \Sigma (\Delta (\Sigma ))^{-1} \end{align*}$

The COPULA Procedure

Normal Copula

Simulation

Fitting