Student's t copula :: SAS/ETS(R) 13.1 User's Guide

Student’s t copula

Subsections:

Simulation
Fitting

Let $\Theta = \{ (\nu , \Sigma ) : \nu \in (1, \infty ), \Sigma \in \mathbb {R}^{m \times m} \}$ and let $t_\nu$ be a univariate t distribution with $\nu$ degrees of freedom.

The Student’s t copula can be written as

$C_{\Theta }(u_1, u_2,{\ldots } u_ m) = \pmb t_{\nu ,\Sigma } \Bigl (t_\nu ^{-1} (u_1), t_\nu ^{-1} (u_2),{\ldots }, t_\nu ^{-1} (u_ m)\Bigr )$

where $\pmb t_{\nu ,\Sigma }$ is the multivariate Student’s t distribution with a correlation matrix $\Sigma$ with $\nu$ degrees of freedom.

Simulation

The input parameters for the simulation are $(\nu , \Sigma )$ . The $t$ copula can be simulated by the following the two steps:

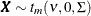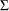Generate a multivariate vector $\bm X \sim t_ m(\nu ,0,\Sigma )$ following the centered t distribution with $\nu$ degrees of freedom and correlation matrix $\Sigma$ .
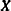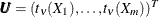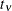Transform the vector $\bm X$ into $\bm U= (t_\nu (X_1),\ldots ,t_\nu (X_ m))^ T$ , where $t_\nu$ is the distribution function of univariate t distribution with $\nu$ degrees of freedom.

To simulate centered multivariate t random variables, you can use the property that $\bm X \sim t_ m(\nu ,0,\Sigma )$ if $\bm X= \sqrt {\nu /s}\bm Z$ , where $\bm Z \sim N(0,\Sigma )$ and the univariate random variable $s \sim \chi ^2_\nu$ .

Fitting

To fit a $t$ copula is to estimate the covariance matrix $\Sigma$ and degrees of freedom $\nu$ from a given multivariate data set. Given a random sample $\pmb { u}_ i = (u_{i,1},\ldots ,u_{i,m})^\top$ , $i=1,\ldots ,n$ that has uniform marginal distributions, the log likelihood is

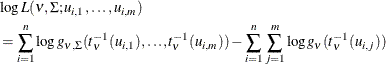
$\begin{align*} & \log L(\nu ,\Sigma ; u_{i,1},\ldots ,u_{i,m}) \\ & = \sum _{i=1}^ n \log g_{\nu ,\Sigma }(t_\nu ^{-1} (u_{i,1}), {\ldots }, t_\nu ^{-1} (u_{i,m})) - \sum _{i=1}^ n\sum _{j=1}^ m \log g_\nu (t_\nu ^{-1}(u_{i,j})) \end{align*}$

where $\nu$ denotes the degrees of freedom of the t copula, $g_{\nu ,\Sigma }$ denotes the joint density function of the centered multivariate t distribution with parameters $(\nu ,\Sigma )$ , $t_\nu$ is the distribution function of a univariate t distribution with $\nu$ degrees of freedom, $\Sigma$ is a correlation matrix, and $g_\nu$ is the density function of univariate t distribution with $\nu$ degrees of freedom.

The log likelihood can be maximized with respect to the parameters $\theta =(\nu ,\Sigma ) \in \Theta$ using numerical optimization. If you allow the parameters in $\Sigma$ to be such that $\Sigma$ is symmetric and with ones on the diagonal, then the MLE estimate for $\Sigma$ might not be positive semidefinite. In that case, you need to apply the adjustment to convert the estimated matrix to positive semidefinite, as shown by McNeil, Frey, and Embrechts (2005), Algorithm 5.55.

When the dimension of the data $m$ increases, the numerical optimization quickly becomes infeasible. It is common practice to estimate the correlation matrix $\Sigma$ by calibration using Kendall’s tau. Then, using this fixed $\Sigma$ , the single parameter $\nu$ can be estimated by MLE. By proposition 5.37 in McNeil, Frey, and Embrechts (2005),

$\rho _\tau (U_ i, U_ j) = \frac{2}{\pi } \textrm{arcsin} \rho _{ij}$

where $\rho _\tau$ is the Kendall’s tau and $\rho _{ij}$ is the off-diagonal elements of the correlation matrix $\Sigma$ of the t copula. Therefore, an estimate for the correlation is

$\hat{\rho }_{ij}= \sin \left(\frac12 \pi \hat{\rho }^\tau _{i,j}\right)$

where $\hat{\rho }$ and $\hat{\rho }^\tau$ are the estimates of the sample correlation matrix and Kendall’s tau, respectively. However, it is possible that the estimate of the correlation matrix $\hat{\Sigma }$ is not positive definite. In this case, there is a standard procedure that uses the eigenvalue decomposition to transform the correlation matrix into one that is positive definite. Let $\Sigma$ be a symmetric matrix with ones on the diagonal, with off-diagonal entries in $[-1,1]$ . If $\Sigma$ is not positive semidefinite, use Algorithm 5.55 from McNeil, Frey, and Embrechts (2005):

Compute the eigenvalue decomposition 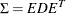$\Sigma = E DE^ T$ , where 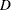$D$ is a diagonal matrix that contains all the eigenvalues and 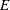$E$ is an orthogonal matrix that contains the eigenvectors.
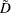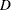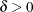Construct a diagonal matrix $\tilde{D}$ by replacing all negative eigenvalues in $D$ by a small value $\delta >0$ .
Compute 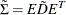$\tilde{\Sigma }=E\tilde{D}E^ T$ , which is positive definite but not necessarily a correlation matrix.
Apply the normalizing operator 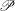$\mathcal{P}$ on the matrix 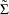$\tilde{\Sigma }$ to obtain the correlation matrix desired.

The log likelihood function and its gradient function for a single observation are listed as follows, where $\bm \zeta =(\zeta _1,\ldots ,\zeta _ m)$ , with $\zeta _ j = t_\nu ^{-1}(u_ j)$ , and $g$ is the derivative of the $\log \Gamma$ function:

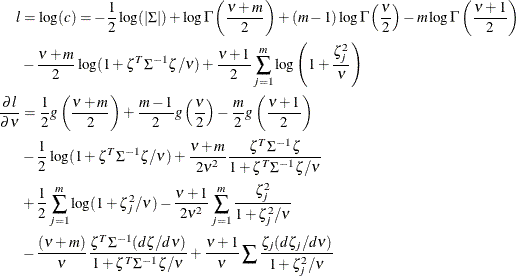
$\begin{align*} l & = \log (c) = -\frac12 \log ( |\Sigma |) +\log \Gamma \left(\frac{\nu +m}{2}\right) +(m-1) \log \Gamma \left(\frac\nu 2 \right) - m \log \Gamma \left(\frac{\nu +1}{2}\right)\\ & -\frac{\nu + m}{2} \log (1+ \zeta ^ T \Sigma ^{-1}\zeta /\nu ) +\frac{\nu +1}{2} \sum _{j=1}^ m \log \left(1+ \frac{\zeta _ j^2}{\nu }\right)\\ \frac{\partial l}{\partial \nu } & = \frac12 g\left(\frac{\nu +m}{2}\right) +\frac{m-1}{2} g\left(\frac\nu 2 \right)-\frac m2 g\left(\frac{\nu +1}{2}\right)\\ & -\frac12 \log (1+\zeta ^ T \Sigma ^{-1}\zeta /\nu ) + \frac{\nu +m}{2\nu ^2} \frac{\zeta ^ T \Sigma ^{-1}\zeta }{1+\zeta ^ T \Sigma ^{-1}\zeta /\nu }\\ & + \frac12 \sum _{j=1}^ m \log (1+\zeta _ j^2/ \nu ) - \frac{\nu +1}{2\nu ^2} \sum _{j=1}^ m \frac{\zeta _ j^2}{1+\zeta _ j^2/\nu }\\ & - \frac{(\nu + m)}{\nu }\frac{\zeta ^ T \Sigma ^{-1}(d\zeta /d \nu )}{1+\zeta ^ T \Sigma ^{-1}\zeta / \nu } +\frac{\nu +1}{\nu } \sum \frac{\zeta _ j (d\zeta _ j /d\nu )}{1+\zeta _ j^2/\nu } \end{align*}$

The derivative of the likelihood with respect to the correlation matrix ${\Sigma }$ follows:

$\begin{align*} \frac{\partial l}{\partial \Sigma }& = -\frac12 (\Sigma ^{-1})^ T +\frac{\nu +m}{2}\frac{\Sigma ^{-T}\zeta \zeta ^ T \Sigma ^{-T}/\nu }{1+ \zeta ^ T \Sigma ^{-1}\zeta /\nu }\\ & =-\frac12 (\Sigma ^{-1})^ T +\frac{\nu +m}{2}\frac{\Sigma ^{-T}\zeta \zeta ^ T \Sigma ^{-T}}{\nu + \zeta ^ T \Sigma ^{-1}\zeta } \end{align*}$

The COPULA Procedure