-
ALPHA=significance-level
-
The ALPHA= option specifies the significance level for tests in the IDENTIFY statement. The default is 0.05.
-
CENTER
-
centers each time series by subtracting its sample mean. The analysis is done on the centered data. Later, when forecasts
are generated, the mean is added back. Note that centering is done after differencing. The CENTER option is normally used
in conjunction with the NOCONSTANT option of the ESTIMATE statement.
-
CLEAR
-
deletes all old models. This option is useful when you want to delete old models so that the input variables are not prewhitened.
(See the section Prewhitening for more information.)
-
CROSSCORR=variable (d11, d12, …, d1k )
-
-
CROSSCORR= (variable (d11, d12, …, d1k )... variable (d21, d22, …, d2k ))
-
names the variables cross-correlated with the response variable given by the VAR= specification.
Each variable name can be followed by a list of differencing lags in parentheses, the same as for the VAR= specification.
If differencing is specified for a variable in the CROSSCORR= list, the differenced series is cross-correlated with the VAR=
option series, and the differenced series is used when the ESTIMATE statement INPUT= option refers to the variable.
-
DATA=SAS-data-set
-
specifies the input SAS data set that contains the time series. If the DATA= option is omitted, the DATA= data set specified
in the PROC ARIMA statement is used; if the DATA= option is omitted from the PROC ARIMA statement as well, the most recently
created data set is used.
-
ESACF
-
computes the extended sample autocorrelation function and uses these estimates to tentatively identify the autoregressive
and moving-average orders of mixed models.
The ESACF option generates two tables. The first table displays extended sample autocorrelation estimates, and the second
table displays probability values that can be used to test the significance of these estimates. The P=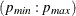 and Q=
and Q=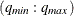 options determine the size of the table.
options determine the size of the table.
The autoregressive and moving-average orders are tentatively identified by finding a triangular pattern in which all values
are insignificant. The ARIMA procedure finds these patterns based on the IDENTIFY statement ALPHA= option and displays possible
recommendations for the orders.
The following code generates an ESACF table with dimensions of p=(0:7) and q=(0:8).
proc arima data=test;
identify var=x esacf p=(0:7) q=(0:8);
run;
See the section The ESACF Method for more information.
-
MINIC
-
uses information criteria or penalty functions to provide tentative ARMA order identification. The MINIC option generates
a table that contains the computed information criterion associated with various ARMA model orders. The PERROR=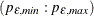 option determines the range of the autoregressive model orders used to estimate the error series. The P=
option determines the range of the autoregressive model orders used to estimate the error series. The P=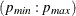 and Q=
and Q=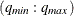 options determine the size of the table. The ARMA orders are tentatively identified by those orders that minimize the information
criterion.
options determine the size of the table. The ARMA orders are tentatively identified by those orders that minimize the information
criterion.
The following statements generate a MINIC table with default dimensions of p=(0:5) and q=(0:5) and with the error series estimated
by an autoregressive model with an order, 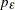 , that minimizes the AIC in the range from 8 to 11.
, that minimizes the AIC in the range from 8 to 11.
proc arima data=test;
identify var=x minic perror=(8:11);
run;
See the section The MINIC Method for more information.
-
NLAG=number
-
indicates the number of lags to consider in computing the autocorrelations and cross-correlations. To obtain preliminary estimates
of an ARIMA(p, d, q ) model, the NLAG= value must be at least p +q +d. The number of observations must be greater than or equal to the NLAG= value. The default value for NLAG= is 24 or one-fourth
the number of observations, whichever is less. Even though the NLAG= value is specified, the NLAG= value can be changed according
to the data set.
-
NOMISS
-
uses only the first continuous sequence of data with no missing values. By default, all observations are used.
-
NOPRINT
-
suppresses the normal printout (including the correlation plots) generated by the IDENTIFY statement.
-
OUTCOV=SAS-data-set
-
writes the autocovariances, autocorrelations, inverse autocorrelations, partial autocorrelations, and cross covariances to
an output SAS data set. If the OUTCOV= option is not specified, no covariance output data set is created. See the section
OUTCOV= Data Set for more information.
-
P=(
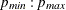 )
)
-
see the ESACF, MINIC, and SCAN options for details.
-
PERROR=(
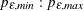 )
)
-
determines the range of the autoregressive model orders used to estimate the error series in MINIC, a tentative ARMA order
identification method. See the section The MINIC Method for more information. By default 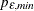 is set to
is set to 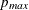 and
and 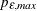 is set to
is set to 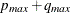 , where
, where 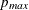 and
and 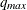 are the maximum settings of the P= and Q= options on the IDENTIFY statement.
are the maximum settings of the P= and Q= options on the IDENTIFY statement.
-
Q=(
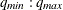 )
)
-
see the ESACF, MINIC, and SCAN options for details.
-
SCAN
-
computes estimates of the squared canonical correlations and uses these estimates to tentatively identify the autoregressive
and moving-average orders of mixed models.
The SCAN option generates two tables. The first table displays squared canonical correlation estimates, and the second table
displays probability values that can be used to test the significance of these estimates. The P=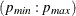 and Q=
and Q=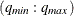 options determine the size of each table.
options determine the size of each table.
The autoregressive and moving-average orders are tentatively identified by finding a rectangular pattern in which all values
are insignificant. The ARIMA procedure finds these patterns based on the IDENTIFY statement ALPHA= option and displays possible
recommendations for the orders.
The following code generates a SCAN table with default dimensions of p=(0:5) and q=(0:5). The recommended orders are based
on a significance level of 0.1.
proc arima data=test;
identify var=x scan alpha=0.1;
run;
See the section The SCAN Method for more information.
-
STATIONARITY=
-
performs stationarity tests. Stationarity tests can be used to determine whether differencing terms should be included in
the model specification. In each stationarity test, the autoregressive orders can be specified by a range, test= 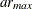 , or as a list of values, test=
, or as a list of values, test= 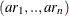 , where test is ADF, PP, or RW. The default is (0,1,2).
, where test is ADF, PP, or RW. The default is (0,1,2).
See the section Stationarity Tests for more information.
-
STATIONARITY=(ADF= AR orders DLAG= s )
STATIONARITY=(DICKEY= AR orders DLAG= s )
-
performs augmented Dickey-Fuller tests. If the DLAG= option is specified with
option is specified with  is greater than one, seasonal Dickey-Fuller tests are performed. The maximum allowable value of
is greater than one, seasonal Dickey-Fuller tests are performed. The maximum allowable value of  is 12. The default value of
is 12. The default value of  is 1. The following code performs augmented Dickey-Fuller tests with autoregressive orders 2 and 5.
is 1. The following code performs augmented Dickey-Fuller tests with autoregressive orders 2 and 5.
proc arima data=test;
identify var=x stationarity=(adf=(2,5));
run;
-
STATIONARITY=(PP= AR orders )
STATIONARITY=(PHILLIPS= AR orders )
-
performs Phillips-Perron tests. The following statements perform augmented Phillips-Perron tests with autoregressive orders ranging from 0 to 6.
proc arima data=test;
identify var=x stationarity=(pp=6);
run;
-
STATIONARITY=(RW=AR orders )
STATIONARITY=(RANDOMWALK=AR orders )
-
performs random-walk-with-drift tests. The following statements perform random-walk-with-drift tests with autoregressive orders ranging from 0 to 2.
proc arima data=test;
identify var=x stationarity=(rw);
run;
-
VAR=variable
VAR= variable ( d1, d2, …, dk )
-
names the variable that contains the time series to analyze. The VAR= option is required.
A list of differencing lags can be placed in parentheses after the variable name to request that the series be differenced
at these lags. For example, VAR=X(1) takes the first differences of X. VAR=X(1,1) requests that X be differenced twice, both
times with lag 1, producing a second difference series, which is 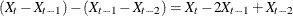 .
.
VAR=X(2) differences X once at lag two 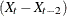 .
.
If differencing is specified, it is the differenced series that is processed by any subsequent ESTIMATE statement.
-
WHITENOISE=ST | IGNOREMISS
-
specifies the type of test statistic that is used in the white noise test of the series when the series contains missing values.
If WHITENOISE=IGNOREMISS, the standard Ljung-Box test statistic is used. If WHITENOISE=ST, a modification of this statistic
suggested by Stoffer and Toloi (1992) is used. The default is WHITENOISE=ST.
 The Three Stages of ARIMA ModelingIdentification StageEstimation and Diagnostic Checking StageForecasting StageUsing ARIMA Procedure StatementsGeneral Notation for ARIMA ModelsStationarityDifferencingSubset, Seasonal, and Factored ARMA ModelsInput Variables and Regression with ARMA ErrorsIntervention Models and Interrupted Time SeriesRational Transfer Functions and Distributed Lag ModelsForecasting with Input VariablesData Requirements
The Three Stages of ARIMA ModelingIdentification StageEstimation and Diagnostic Checking StageForecasting StageUsing ARIMA Procedure StatementsGeneral Notation for ARIMA ModelsStationarityDifferencingSubset, Seasonal, and Factored ARMA ModelsInput Variables and Regression with ARMA ErrorsIntervention Models and Interrupted Time SeriesRational Transfer Functions and Distributed Lag ModelsForecasting with Input VariablesData Requirements
 The Inverse Autocorrelation FunctionThe Partial Autocorrelation FunctionThe Cross-Correlation FunctionThe ESACF MethodThe MINIC MethodThe SCAN MethodStationarity TestsPrewhiteningIdentifying Transfer Function ModelsMissing Values and AutocorrelationsEstimation DetailsSpecifying Inputs and Transfer FunctionsInitial ValuesStationarity and InvertibilityNaming of Model ParametersMissing Values and Estimation and ForecastingForecasting DetailsForecasting Log Transformed DataSpecifying Series PeriodicityDetecting OutliersOUT= Data SetOUTCOV= Data SetOUTEST= Data SetOUTMODEL= SAS Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesStatistical Graphics
The Inverse Autocorrelation FunctionThe Partial Autocorrelation FunctionThe Cross-Correlation FunctionThe ESACF MethodThe MINIC MethodThe SCAN MethodStationarity TestsPrewhiteningIdentifying Transfer Function ModelsMissing Values and AutocorrelationsEstimation DetailsSpecifying Inputs and Transfer FunctionsInitial ValuesStationarity and InvertibilityNaming of Model ParametersMissing Values and Estimation and ForecastingForecasting DetailsForecasting Log Transformed DataSpecifying Series PeriodicityDetecting OutliersOUT= Data SetOUTCOV= Data SetOUTEST= Data SetOUTMODEL= SAS Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesStatistical Graphics