The HETERO statement specifies variables that are related to the heteroscedasticity of the residuals and the way these variables
are used to model the error variance of the regression.
The heteroscedastic regression model supported by the HETERO statement is
The HETERO statement specifies a model for the conditional variance 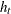 . The vector
. The vector 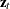 is composed of the variables listed in the HETERO statement,
is composed of the variables listed in the HETERO statement, 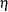 is a parameter vector, and
is a parameter vector, and 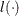 is a link function that depends on the value of the LINK= option. In the printed output,
is a link function that depends on the value of the LINK= option. In the printed output, 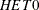 represents the estimate of sigma, while
represents the estimate of sigma, while 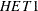 -
- 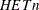 are the estimates of parameters in the
are the estimates of parameters in the 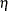 vector.
vector.
The keyword XBETA can be used in the variables list to refer to the model predicted value 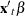 . If XBETA is specified in the variables list, other variables in the HETERO statement will be ignored. In addition, XBETA cannot be specified in the GARCH process.
. If XBETA is specified in the variables list, other variables in the HETERO statement will be ignored. In addition, XBETA cannot be specified in the GARCH process.
For heteroscedastic regression models without GARCH effects, the errors 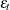 are assumed to be uncorrelated — the heteroscedasticity models specified by the HETERO statement cannot be combined with
an autoregressive model for the errors. Thus, when a HETERO statement is used, the NLAG= option cannot be specified unless
the GARCH= option is also specified.
are assumed to be uncorrelated — the heteroscedasticity models specified by the HETERO statement cannot be combined with
an autoregressive model for the errors. Thus, when a HETERO statement is used, the NLAG= option cannot be specified unless
the GARCH= option is also specified.
You can specify the following options in the HETERO statement.
-
LINK=value
-
specifies the functional form of the heteroscedasticity model. By default, LINK=EXP. If you specify a GARCH model with the
HETERO statement, the model is estimated using LINK= LINEAR only. For details, see the section Using the HETERO Statement with GARCH Models. Values of the LINK= option are as follows:
- EXP
-
specifies the exponential link function. The following model is estimated when you specify LINK=EXP:
- SQUARE
-
specifies the square link function. The following model is estimated when you specify LINK=SQUARE:
- LINEAR
-
specifies the linear function; that is, the HETERO statement variables predict the error variance linearly. The following
model is estimated when you specify LINK=LINEAR:
-
COEF=value
-
imposes constraints on the estimated parameters 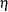 of the heteroscedasticity model. You can specify the following values:
of the heteroscedasticity model. You can specify the following values:
- NONNEG
-
specifies that the estimated heteroscedasticity parameters 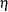 must be nonnegative.
must be nonnegative.
- UNIT
-
constrains all heteroscedasticity parameters 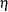 to equal 1.
to equal 1.
- ZERO
-
constrains all heteroscedasticity parameters 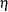 to equal 0.
to equal 0.
- UNREST
-
specifies unrestricted estimation of 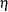 .
.
If you specify the GARCH= option in the MODEL statement, the default is COEF=NONNEG. If you do not specify the GARCH= option
in the MODEL statement, the default is COEF=UNREST.
-
STD=value
-
imposes constraints on the estimated standard deviation  of the heteroscedasticity model. You can specify the following values:
of the heteroscedasticity model. You can specify the following values:
- NONNEG
-
specifies that the estimated standard deviation parameter  must be nonnegative.
must be nonnegative.
- UNIT
-
constrains the standard deviation parameter  to equal 1.
to equal 1.
- UNREST
-
specifies unrestricted estimation of  .
.
The default is STD=UNREST.
-
TEST=LM
-
produces a Lagrange multiplier test for heteroscedasticity. The null hypothesis is homoscedasticity; the alternative hypothesis
is heteroscedasticity of the form specified by the HETERO statement. The power of the test depends on the variables specified
in the HETERO statement.
The test may give different results depending on the functional form specified by the LINK= option. However, in many cases
the test does not depend on the LINK= option. The test is invariant to the form of 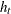 when
when 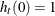 and
and 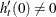 . (The condition
. (The condition 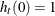 is satisfied except when the NOCONST option is specified with LINK=SQUARE or LINK=LINEAR.)
is satisfied except when the NOCONST option is specified with LINK=SQUARE or LINK=LINEAR.)
-
NOCONST
-
specifies that the heteroscedasticity model does not include the unit term for the LINK=SQUARE and LINK=LINEAR options. For
example, the following model is estimated when you specify the options LINK=SQUARE NOCONST:


 Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics
Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics
![]() . The vector
. The vector ![]() is composed of the variables listed in the HETERO statement,
is composed of the variables listed in the HETERO statement, ![]() is a parameter vector, and
is a parameter vector, and ![]() is a link function that depends on the value of the LINK= option. In the printed output,
is a link function that depends on the value of the LINK= option. In the printed output, ![]() represents the estimate of sigma, while
represents the estimate of sigma, while ![]() -
- ![]() are the estimates of parameters in the
are the estimates of parameters in the ![]() vector.
vector.
![]() . If XBETA is specified in the variables list, other variables in the HETERO statement will be ignored. In addition, XBETA cannot be specified in the GARCH process.
. If XBETA is specified in the variables list, other variables in the HETERO statement will be ignored. In addition, XBETA cannot be specified in the GARCH process.
![]() are assumed to be uncorrelated — the heteroscedasticity models specified by the HETERO statement cannot be combined with
an autoregressive model for the errors. Thus, when a HETERO statement is used, the NLAG= option cannot be specified unless
the GARCH= option is also specified.
are assumed to be uncorrelated — the heteroscedasticity models specified by the HETERO statement cannot be combined with
an autoregressive model for the errors. Thus, when a HETERO statement is used, the NLAG= option cannot be specified unless
the GARCH= option is also specified.