The ENTROPY Procedure (Experimental)

Maximum Entropy-Based Seemingly Unrelated Regression

In a multivariate regression model, the errors in different equations might be correlated. In this case, the efficiency of the estimation can be improved by taking these cross-equation correlations into account. Seemingly unrelated regression (SUR), also called joint generalized least squares (JGLS) or Zellner estimation, is a generalization of OLS for multi-equation systems.

Like SUR in the least squares setting, the generalized maximum entropy SUR (GME-SUR) method assumes that all the regressors are independent variables and uses the correlations among the errors in different equations to improve the regression estimates. The GME-SUR method requires an initial entropy regression to compute residuals. The entropy residuals are used to estimate the cross-equation covariance matrix.

In the iterative GME-SUR (ITGME-SUR) case, the preceding process is repeated by using the residuals from the GME-SUR estimation to estimate a new cross-equation covariance matrix. ITGME-SUR method alternates between estimating the system coefficients and estimating the cross-equation covariance matrix until the estimated coefficients and covariance matrix converge.

The estimation problem becomes the generalized maximum entropy system adapted for multi-equations as follows:

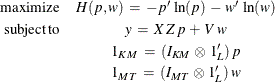
\begin{eqnarray*} \mr{maximize} & H(p,w) \: = \: -p’ \, \ln (p) \: - \: w’ \, \ln (w) \\ \mr{subject\, to} & y \: = \: X \, Z \, p \: + \: V \, w \\ & 1_{KM} \: = \: (I_{KM} \, \otimes \, 1_{L}’) \, p \\ & 1_{MT} \: = \: (I_{MT} \, \otimes \, 1_{L}’) \, w \end{eqnarray*}

where

\[ \beta \: = \: Z \, p \]
\[ \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \ \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! Z \: = \: \left[ \begin{array}{ccccccccccccccc} z_{11}^{1} & \cdot \cdot \cdot & z_{L1}^{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \ddots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & z_{11}^{K} & \cdot \cdot \cdot & z_{L1}^{K} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddots & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & z_{1M}^{1} & \cdot \cdot \cdot & z_{LM}^{1} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddots & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & z_{1M}^{K} & \cdot \cdot \cdot & z_{LM}^{K} \end{array} \right] \]
\[ p \: = \: \left[ \begin{array}{ccccccccccccccc} p_{11}^{1} & \cdot & p_{L1}^{1} & \cdot & p_{11}^{K} & \cdot & p_{L1}^{K} & \cdot & p_{1M}^{1} & \cdot & p_{LM}^{1} & \cdot & p_{1M}^{K} & \cdot & p_{LM}^{K} \end{array} \right]’ \]
\[ e \: = \: V \, w \]
\[ \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \ \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! V \: = \: \left[ \begin{array}{ccccccccccccccc} v_{11}^{1} & \cdot \cdot \cdot & v_{11}^{L} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \ddots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & v_{1T}^{1} & \cdot \cdot \cdot & v_{1T}^{L} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddots & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & v_{M1}^{1} & \cdot \cdot \cdot & v_{M1}^{L} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddots & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & v_{MT}^{1} & \cdot \cdot \cdot & v_{MT}^{L} \end{array} \right] \]
\[ \! \! \! \! \! \! \! \! \! \! w \: = \: \left[ \begin{array}{ccccccccccccccc} w_{11}^{1} & \cdot & w_{11}^{L} & \cdot & w_{1T}^{1} & \cdot & w_{1T}^{L} & \cdot & w_{M1}^{1} & \cdot & w_{M1}^{L} & \cdot & w_{MT}^{1} & \cdot & w_{MT}^{L} \end{array} \right]’ \, \]

y denotes the MT column vector of observations of the dependent variables; $\mb{X}$ denotes the (MT x KM ) matrix of observations for the independent variables; p denotes the LKM column vector of weights associated with the points in Z; w denotes the LMT column vector of weights associated with the points in V; $1_{L}$, $1_{KM}$, and $1_{MT}$ are L-, KM-, and MT-dimensional column vectors, respectively, of ones; and $\mb{I_{KM}}$ and $\mb{I_{MT}}$ are (KM x KM) and (MT x MT) dimensional identity matrices. The subscript l denotes the support point $(l=1, 2, \ldots , L)$, k denotes the parameter $(k=1, 2, \ldots , K)$, m denotes the equation $(m=1, 2, \ldots , M)$, and t denotes the observation $(t=1, 2, \ldots ,T)$.

Using this notation, the maximum entropy problem that is analogous to the OLS problem used as the initial step of the traditional SUR approach is

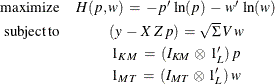
\begin{eqnarray*} \mr{maximize} & H(p,w) \: = \: -p’ \, \ln (p) \: - \: w’ \, \ln (w) \\ \mr{subject\, to} & \, (y \: - \: X \, Z \, p ) \: = \sqrt {\Sigma } \: V \, w \\ & 1_{KM} \: = \: (I_{KM} \, \otimes \, 1_{L}’) \, p \\ & 1_{MT} \: = \: (I_{MT} \, \otimes \, 1_{L}’) \, w \end{eqnarray*}

The results are GME-SUR estimates with independent errors, the analog of OLS. The covariance matrix $\hat{\Sigma }$ is computed based on the residual of the equations, $Vw=e$. An $L’L$ factorization of the $\hat{\Sigma }$ is used to compute the square root of the matrix.

After solving this problem, these entropy-based estimates are analogous to the Aitken two-step estimator. For iterative GME-SUR, the covariance matrix of the errors is recomputed, and a new $\hat{\Sigma }$ is computed and factored. As in traditional ITSUR, this process repeats until the covariance matrix and the parameter estimates converge.

The estimation of the parameters for the normed-moment version of SUR (GME-SUR-NM) uses an identical process. The constraints for GME-SUR-NM is defined as:

\[ X’y \: = \: X’(\mb{S} ^{-1} {\otimes } \mb{I} )X \, Z \, p \: + \: X’(\mb{S} ^{-1} {\otimes } \mb{I} )V \, w \]

The estimation of the parameters for GME-SUR-NM uses an identical process as outlined previously for GME-SUR.