The ENTROPY Procedure (Experimental)
- Overview
-
Getting Started

-
Syntax

-
Details
 Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics
Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics -
Examples

- References
The ENTROPY procedure implements a parametric method of linear estimation based on generalized maximum entropy. The ENTROPY procedure is suitable when there are outliers in the data and robustness is required, when the model is ill-posed or under-determined for the observed data, or for regressions that involve small data sets.
The main features of the ENTROPY procedure are as follows:
-
estimation of simultaneous systems of linear regression models
-
estimation of Markov models
-
estimation of seemingly unrelated regression (SUR) models
-
estimation of unordered multinomial discrete Choice models
-
solution of pure inverse problems
-
allowance of bounds and restrictions on parameters
-
performance of tests on parameters
-
allowance of data and moment constrained generalized cross entropy
It is often the case that the statistical/economic model of interest is ill-posed or under-determined for the observed data. For the general linear model, this can imply that high degrees of collinearity exist among explanatory variables or that there are more parameters to estimate than observations available to estimate them. These conditions lead to high variances or non-estimability for traditional generalized least squares (GLS) estimates.
Under these situations it might be in the researcher’s or practitioner’s best interest to consider a nontraditional technique for model fitting. The principle of maximum entropy is the foundation for an estimation methodology that is characterized by its robustness to ill-conditioned designs and its ability to fit over-parameterized models. See Mittelhammer, Judge, and Miller (2000) and Golan, Judge, and Miller (1996) for a discussion of Shannon’s maximum entropy measure and the related Kullback-Leibler information.
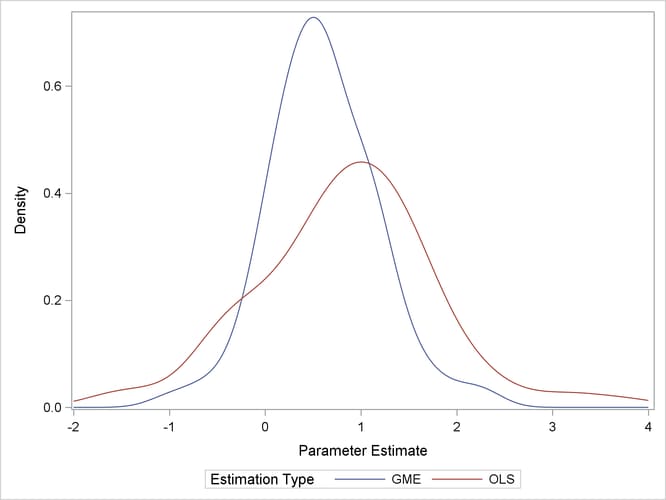
Generalized maximum entropy (GME) is a means of selecting among probability distributions to choose the distribution that maximizes uncertainty or uniformity remaining in the distribution, subject to information already known about the distribution. Information takes the form of data or moment constraints in the estimation procedure. PROC ENTROPY creates a GME distribution for each parameter in the linear model, based upon support points supplied by the user. The mean of each distribution is used as the estimate of the parameter. Estimates tend to be biased, as they are a type of shrinkage estimate, but typically portray smaller variances than ordinary least squares (OLS) counterparts, making them more desirable from a mean squared error viewpoint (see Figure 13.1).
Maximum entropy techniques are most widely used in the econometric and time series fields. Some important uses of maximum entropy include the following:
-
size distribution of firms
-
stationary Markov Process
-
social accounting matrix (SAM)
-
consumer brand preference
-
exchange rate regimes
-
wage-dependent firm relocation
-
oil market dynamics