The OPTLSO Procedure

Overview: OPTLSO Procedure

The OPTLSO procedure performs optimization of general nonlinear functions that are defined by the FCMP procedure in Base SAS over both continuous and integer variables. These functions do not need to be expressed in analytic closed form, and they can be non-smooth, discontinuous, and computationally expensive to evaluate. Problem types can be single-objective or multiobjective. PROC OPTLSO runs in either single-machine mode or distributed mode.

Note: Distributed mode requires SAS High-Performance Optimization.

The general problem formulation is given by

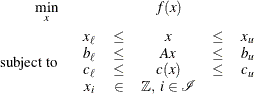
$\begin{eqnarray*} \min _ x & f(x) \\ \mr {subject\ to} & \begin{array}{cccccc} x_\ell & \le & x & \le & x_ u \\ b_\ell & \le & Ax & \le & b_ u \\ c_\ell & \le & c(x) & \le & c_ u \\ x_ i & \in & \mathbb {Z},\; i \in {\mathcal I} \end{array}\end{eqnarray*}$

where $x \in {\mathbb R}^ n$ is the vector of the decision variables; $f(x): {\mathbb R}^ n \to {\mathbb R}$ is the objective function; $A$ is an $m \times n$ linear coefficient matrix; $c(x): {\mathbb R}^ n \to {\mathbb R}^ p$ is the vector of general nonlinear constraint functions—that is, $c = (c_{1}, \ldots , c_{p})$ ; $x_\ell$ and $x_ u$ are the vectors of the lower and upper bounds, respectively, on the decision variables; $b_\ell$ and $b_ u$ are the vectors of the lower and upper bounds, respectively, on the linear constraints; and $c_\ell$ and $c_ u$ are the vectors of the lower and upper bounds, respectively, on the nonlinear constraint functions. Equality constraints can be represented by equating the lower and upper bounds of the desired variable or constraint.

Because of the limited assumptions that are made on the objective function $f(x)$ and constraint functions $c(x)$ , the OPTLSO procedure uses a parallel hybrid derivative-free approach similar to approaches that are used in Taddy et al. (2009); Plantenga (2009); Gray, Fowler, and Griffin (2010); Griffin and Kolda (2010a). Derivative-free methods are effective whether or not derivatives are available, provided that the dimension of $x$ is not too large (Gray and Fowler, 2011). As a rule of thumb, derivative-free algorithms are rarely applied to black-box optimization problems that have more than 100 variables. The term black box emphasizes that the function is used only as a mapping operator and makes no implicit assumption about or requirement on the structure of the functions themselves. In contrast, derivative-based algorithms commonly require the nonlinear objectives and constraints to be continuous and smooth and to have an exploitable analytic representation.

The OPTLSO procedure solves general nonlinear problems by simultaneously applying multiple instances of global and local search algorithms in parallel. This streamlines the process of needing to first apply a global algorithm in order to determine a good starting point to initialize a local algorithm. For example, if the problem is convex, a local algorithm should be sufficient, and the application of the global algorithm would create unnecessary overhead. If the problem instead has many local minima, failing to run a global search algorithm first could result in an inferior solution. Rather than attempting to guess which paradigm is best, PROC OPTLSO simultaneously performs global and local searches while continuously sharing computational resources and function evaluations. The resulting run time and solution quality should be similar to having automatically selected the best global and local search combination, given a suitable number of threads and processors. Moreover, because information is shared, the robustness of the hybrid approach can be increased over hybrid combinations that simply use the output of one algorithm to hot-start the second algorithm. In this chapter, the term solver refers to an implementation of one or more algorithms that can be used to solve a problem.

The OPTLSO procedure uses different strategies to handle different types of constraints. Linear constraints are handled by using both linear programming and strategies similar to those in Griffin, Kolda, and Lewis (2008), where tangent directions to nearby constraints are constructed and used as search directions. Nonlinear constraints are handled by using smooth merit functions (Griffin and Kolda, 2010b). Integer and categorical variables are handled by using strategies and concepts similar to those in Griffin et al. (2011). This approach can be viewed as a genetic algorithm that includes an additional “growth” step, in which selected points from the population are allotted a small fraction of the total evaluation budget to improve their fitness score (that is, the objective function value) by using local optimization over the continuous variables.

Because the OPTLSO procedure is a high-performance analytical procedure, it also does the following:

enables you to run in distributed mode on a cluster of machines that distribute the data and the computations
enables you to run in single-machine mode on the server where SAS is installed
exploits all the available cores and concurrent threads, regardless of execution mode

For more information, see Chapter 4: Shared Concepts and Topics in SAS/OR User's Guide: Mathematical Programming, and Chapter 3: Shared Concepts and Topics in Base SAS 9.4 Procedures Guide: High-Performance Procedures, Second Edition, for more information about the options available for the PERFORMANCE statement.