The OPTNET Procedure

Minimum-Cost Network Flow

Subsections:

Minimum Cost Network Flow for a Simple Directed Graph

The minimum-cost network flow problem (MCF) is a fundamental problem in network analysis that involves sending flow over a network at minimal cost. Let $G=(N,A)$ be a directed graph. For each link $(i,j) \in A$ , associate a cost per unit of flow, designated by $c_{ij}$ . The demand (or supply) at each node $i \in N$ is designated as $b_ i$ , where $b_ i \geq 0$ denotes a supply node and $b_ i < 0$ denotes a demand node. These values must be within $[b_ i^ l, b_ i^ u]$ . Define decision variables $x_{ij}$ that denote the amount of flow sent between node $i$ and node $j$ . The amount of flow that can be sent across each link is bounded to be within $[l_{ij}, u_{ij}]$ . The problem can be modeled as a linear programming problem as follows:

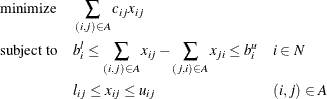
$\begin{alignat*}{3}& \text {minimize} & & \quad \sum _{(i,j) \in A} c_{ij} x_{ij} \\ & \text {subject to} & & \quad b_ i^ l \leq \sum _{(i,j) \in A} x_{ij} - \sum _{(j,i) \in A} x_{ji} \leq b^ u_ i & & \quad i \in N\\ & & & \quad l_{ij} \le x_{ij} \le u_{ij} & & \quad (i,j) \in A \end{alignat*}$

When $b_ i=b_ i^ l=b_ i^ u$ for all nodes $i \in N$ , the problem is called a pure network flow problem. For these problems, the sum of the supplies and demands must be equal to 0 to ensure that a feasible solution exists.

In PROC OPTNET, you can invoke the minimum-cost network flow solver by using the MINCOSTFLOW statement. The options for this statement are described in the section MINCOSTFLOW Statement.

The minimum-cost network flow solver reports status information in a macro variable called _OROPTNET_MCF_. See the section Macro Variable _OROPTNET_MCF_ for more information about this macro variable.

The algorithm that the PROC OPTNET uses for solving MCF is a variant of the primal network simplex algorithm (Ahuja, Magnanti, and Orlin 1993). Sometimes the directed graph $G$ is disconnected. In this case, the problem is first decomposed into its weakly connected components, and then each minimum-cost flow problem is solved separately.

The input for the network is the standard graph input, which is described in the section Graph Input Data. The links data set, which is specified in the DATA_LINKS= option in the PROC OPTNET statement, contains the following columns:

weight defines the link cost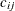 $c_{ij}$ .
lower defines the link lower bound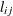 $l_{ij}$ . The default is 0.
upper defines the link upper bound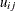 $u_{ij}$ . The default is $\infty$ .

The nodes data set, which is specified in the DATA_NODES= option in the PROC OPTNET statement, can contain the following columns:

weight defines the node supply lower bound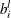 $b_ i^ l$ . The default is 0.
weight2 defines the node supply upper bound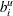 $b_ i^ u$ . The default is $\infty$ .

To define a pure network where the node supply must be met exactly, use the weight variable only. You do not need to specify all the node supply bounds. For any missing node, the solver uses a lower and upper bound of 0.

The resulting optimal flow through the network is written to the links output data set, which is specified in the OUT_LINKS= option in the PROC OPTNET statement.

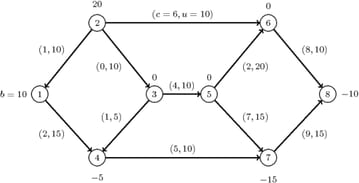
Minimum Cost Network Flow for a Simple Directed Graph

The following example demonstrates how to use the network simplex solver to find a minimum-cost flow in a directed graph. Consider the directed graph in Figure 2.35, which appears in Ahuja, Magnanti, and Orlin (1993).

Figure 2.35: Minimum-Cost Network Flow Problem: Data

The directed graph $G$ can be represented by the following links data set LinkSetIn and nodes data set NodeSetIn.

data LinkSetIn;
   input from to weight upper;
   datalines;
1 4 2 15
2 1 1 10
2 3 0 10
2 6 6 10
3 4 1  5
3 5 4 10
4 7 5 10
5 6 2 20
5 7 7 15
6 8 8 10
7 8 9 15
;

data NodeSetIn;
   input node weight;
   datalines;
1  10
2  20
4  -5
7 -15
8 -10
;

You can use the following call to PROC OPTNET to find a minimum-cost flow:

proc optnet
   loglevel        = moderate
   graph_direction = directed
   data_links      = LinkSetIn
   data_nodes      = NodeSetIn
   out_links       = LinkSetOut;
   mincostflow
      logfreq      = 1;
run;
%put &_OROPTNET_;
%put &_OROPTNET_MCF_;

The progress of the procedure is shown in Figure 2.36.

Figure 2.36: PROC OPTNET Log for Minimum-Cost Network Flow

NOTE: --------------------------------------------------------------------------

NOTE: Running OPTNET version 13.1.

NOTE: --------------------------------------------------------------------------

NOTE: Reading the links data set.

NOTE: Reading the nodes data set.

NOTE: There were 5 observations read from the data set WORK.NODESETIN.

NOTE: There were 11 observations read from the data set WORK.LINKSETIN.

NOTE: Data input used 0.01 (cpu: 0.00) seconds.

NOTE: Building the input graph storage used 0.00 (cpu: 0.00) seconds.

NOTE: The input graph storage is using 0.0 MBs of memory.

NOTE: The number of nodes in the input graph is 8.

NOTE: The number of links in the input graph is 11.

NOTE: --------------------------------------------------------------------------

NOTE: Processing the minimum cost network flow problem.

NOTE: The network has 1 connected component.

Primal Primal Dual

Iteration Objective Infeasibility Infeasibility Time

1 0.000000E+00 2.000000E+01 8.900000E+01 0.00

2 0.000000E+00 2.000000E+01 8.900000E+01 0.00

3 5.000000E+00 1.500000E+01 8.400000E+01 0.00

4 5.000000E+00 1.500000E+01 8.300000E+01 0.00

5 7.500000E+01 1.500000E+01 8.300000E+01 0.00

6 7.500000E+01 1.500000E+01 7.900000E+01 0.00

7 1.300000E+02 1.000000E+01 7.600000E+01 0.00

8 2.700000E+02 0.000000E+00 0.000000E+00 0.00

NOTE: The Network Simplex solve time is 0.00 seconds.

NOTE: The minimum cost network flow is 270.

NOTE: Processing the minimum cost network flow problem used 0.00 (cpu: 0.00)

seconds.

NOTE: --------------------------------------------------------------------------

NOTE: Creating links data set output.

NOTE: Data output used 0.00 (cpu: 0.00) seconds.

NOTE: --------------------------------------------------------------------------

NOTE: The data set WORK.LINKSETOUT has 11 observations and 5 variables.

STATUS=OK MCF=OPTIMAL

STATUS=OPTIMAL OBJECTIVE=270 CPU_TIME=0.00 REAL_TIME=0.00

The optimal solution is displayed in Figure 2.37.

Figure 2.37: Minimum-Cost Network Flow Problem: Optimal Solution

Obs	from	to	upper	weight	mcf_flow
1	1	4	15	2	10
2	2	1	10	1	0
3	2	3	10	0	10
4	2	6	10	6	10
5	3	4	5	1	5
6	3	5	10	4	5
7	4	7	10	5	10
8	5	6	20	2	0
9	5	7	15	7	5
10	6	8	10	8	10
11	7	8	15	9	0

The optimal solution is represented graphically in Figure 2.38.

Figure 2.38: Minimum-Cost Network Flow Problem: Optimal Solution

Obs	from	to	upper	weight	mcf_flow
1	1	4	15	2	10
2	2	1	10	1	0
3	2	3	10	0	10
4	2	6	10	6	10
5	3	4	5	1	5
6	3	5	10	4	5
7	4	7	10	5	10
8	5	6	20	2	0
9	5	7	15	7	5
10	6	8	10	8	10
11	7	8	15	9	0

Obs	from	to	upper	weight	mcf_flow
1	1	4	15	2	10
2	2	1	10	1	0
3	2	3	10	0	10
4	2	6	10	6	10
5	3	4	5	1	5
6	3	5	10	4	5
7	4	7	10	5	10
8	5	6	20	2	0
9	5	7	15	7	5
10	6	8	10	8	10
11	7	8	15	9	0

Obs	from	to	upper	weight	mcf_flow
1	1	4	15	2	10
2	2	1	10	1	0
3	2	3	10	0	10
4	2	6	10	6	10
5	3	4	5	1	5
6	3	5	10	4	5
7	4	7	10	5	10
8	5	6	20	2	0
9	5	7	15	7	5
10	6	8	10	8	10
11	7	8	15	9	0