PROBPLOT Statement: CAPABILITY Procedure

Example 5.19 Displaying a Normal Reference Line

See CAPPROB4 in the SAS/QC Sample LibraryMeasurements of the distance between two holes cut into 50 steel sheets are saved as values of the variable Distance in the following data set:

data Sheets;
   input Distance @@;
   label Distance='Hole Distance in cm';
   datalines;
 9.80 10.20 10.27  9.70  9.76
10.11 10.24 10.20 10.24  9.63
 9.99  9.78 10.10 10.21 10.00
 9.96  9.79 10.08  9.79 10.06
10.10  9.95  9.84 10.11  9.93
10.56 10.47  9.42 10.44 10.16
10.11 10.36  9.94  9.77  9.36
 9.89  9.62 10.05  9.72  9.82
 9.99 10.16 10.58 10.70  9.54
10.31 10.07 10.33  9.98 10.15
;

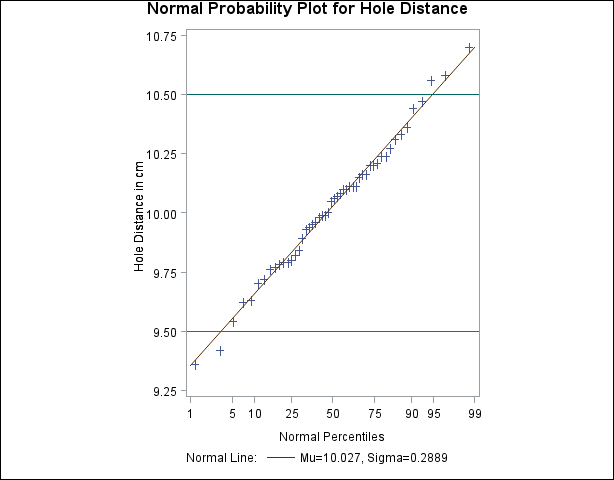
The cutting process is in control, and you decide to check whether the process distribution is normal. The following statements create a normal probability plot for Distance with lower and upper specification lines at 9.5 cm and 10.5 cm:

ods graphics off;
symbol v=plus height=3.5pct;
title 'Normal Probability Plot for Hole Distance';
proc capability data=Sheets noprint;
   spec lsl=9.5 usl=10.5;
   probplot Distance / normal(mu=est sigma=est)
                       square
                       nospeclegend;
run;

The plot is shown in Output 5.19.1. The MU= and SIGMA= normal-options request the diagonal reference line that corresponds to the normal distribution with estimated parameters $\hat{\mu }=10.027$ and $\hat{\sigma }=0.2889$ . The LSL= and USL= SPEC statement options request the lower and upper specification lines. The SYMBOL statement specifies the symbol marker for the plotted points.

Output 5.19.1: Normal Reference Line