QQPLOT Statement: CAPABILITY Procedure

Construction of Quantile-Quantile and Probability Plots

Figure 5.43 illustrates how a Q-Q plot is constructed. First, the n nonmissing values of the variable are ordered from smallest to largest:

$x_{(1)} \leq x_{(2)} \leq \cdots \leq x_{(n)}$

Then the ith ordered value $x_{(i)}$ is represented on the plot by a point whose y-coordinate is $x_{(i)}$ and whose x-coordinate is $F^{-1}\left( \frac{i- 0.375 }{n + 0.25} \right)$ , where $F(\cdot )$ is the theoretical distribution with zero location parameter and unit scale parameter.

Figure 5.43: Construction of a Q-Q Plot

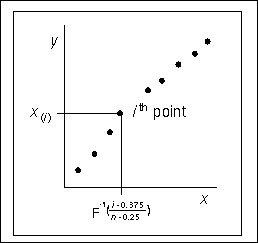
You can modify the adjustment constants –0.375 and 0.25 with the RANKADJ= and NADJ= options. This default combination is recommended by Blom (1958). For additional information, refer to Chambers et al. (1983). Since $x_{(i)}$ is a quantile of the empirical cumulative distribution function (ecdf), a Q-Q plot compares quantiles of the ecdf with quantiles of a theoretical distribution. Probability plots (see PROBPLOT Statement: CAPABILITY Procedure) are constructed the same way, except that the x-axis is scaled nonlinearly in percentiles.