Details and Examples: PARETO Procedure
-
Details

-
Examples
 Creating Before-and-After Pareto ChartsCreating Two-Way Comparative Pareto ChartsHighlighting the Vital FewHighlighting Combinations of CategoriesHighlighting Combinations of CellsOrdering Rows and Columns in a Comparative Pareto ChartMerging Columns in a Comparative Pareto ChartCreating Weighted Pareto ChartsAlternative Pareto Charts
Creating Before-and-After Pareto ChartsCreating Two-Way Comparative Pareto ChartsHighlighting the Vital FewHighlighting Combinations of CategoriesHighlighting Combinations of CellsOrdering Rows and Columns in a Comparative Pareto ChartMerging Columns in a Comparative Pareto ChartCreating Weighted Pareto ChartsAlternative Pareto Charts
Example 15.1 Creating Before-and-After Pareto Charts
See PARETO7 in the SAS/QC Sample LibraryDuring the manufacture of a metal-oxide semiconductor (MOS) capacitor, causes of failures were recorded before and after a
tube in the diffusion furnace was cleaned. This information was saved in a SAS data set named Failure3.
data Failure3; length Cause $ 16 Stage $ 16; label Cause = 'Cause of Failure'; input Stage & $ Cause & $ Counts; datalines; Before Cleaning Contamination 14 Before Cleaning Corrosion 2 Before Cleaning Doping 1 Before Cleaning Metallization 2 Before Cleaning Miscellaneous 3 Before Cleaning Oxide Defect 8 Before Cleaning Silicon Defect 1 After Cleaning Doping 0 After Cleaning Corrosion 2 After Cleaning Metallization 4 After Cleaning Miscellaneous 2 After Cleaning Oxide Defect 1 After Cleaning Contamination 12 After Cleaning Silicon Defect 2 ;
To compare distribution of failures before and after cleaning, you can create two separate Pareto charts, one for the observations
in which Stage is equal to 'Before Cleaning' and one for the observations in which Stage is equal to 'After Cleaning'. You can do this with the BY statement.
proc sort data=Failure3; by Stage; run;
ods graphics off;
title 'Pareto Effect of Furnace Tube';
proc pareto data=Failure3;
vbar Cause / freq = Counts
angle = -60;
by Stage;
run;
The SORT procedure sorts the observations in order of the values of Stage. It is not necessary to sort by the values of Cause since this is done by the PARETO procedure. The two charts, displayed in Output 15.1.1 and Output 15.1.2, reveal a reduction in oxide defects after the tube was cleaned. This is a relative reduction, since the primary axes are
scaled in percent units.
Output 15.1.1: “After” Analysis Using Stage as a BY Variable
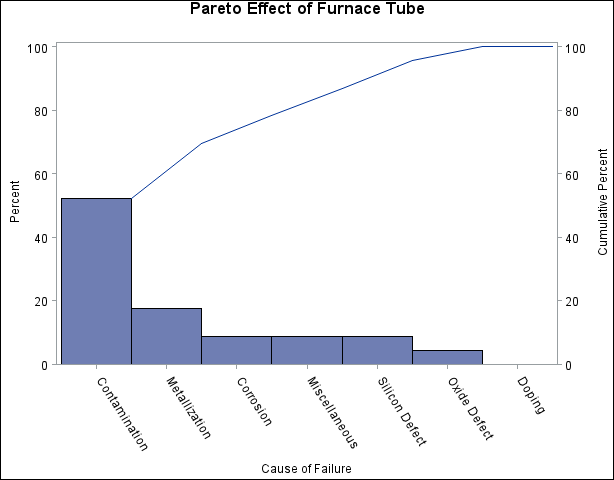
Output 15.1.2: “Before” Analysis Using Stage as a BY Variable
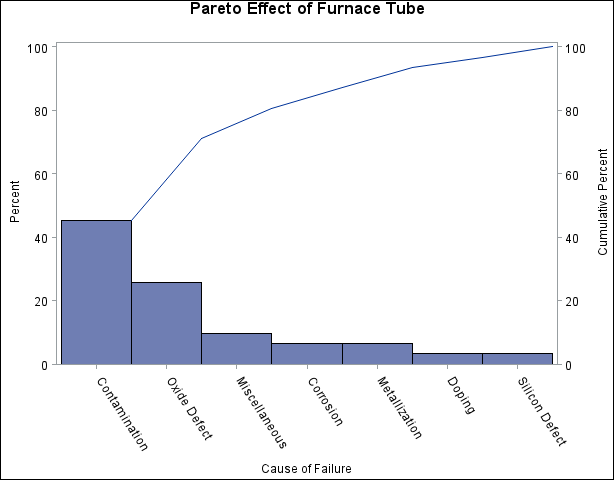
In general, it is difficult to compare Pareto charts created with BY processing because their axes are not necessarily uniform. A better approach is to construct a comparative Pareto chart, as illustrated by the following statements:
goptions vsize=4.25 in htext=2.8 pct htitle=3.2 pct;
title 'Comparison of IC Failures';
proc pareto data=Failure3;
vbar Cause / class = Stage
freq = Counts
scale = percent
intertile = 1.0
classkey = 'Before Cleaning';
run;
See PARETO8 in the SAS/QC Sample LibraryThe CLASS= option designates Stage as a classification variable, and this directs the procedure to create the one-way comparative Pareto chart, shown in Output 15.1.3, that displays a component chart for each level of Stage.
Output 15.1.3: Before-and-After Analysis Using Comparative Pareto Chart
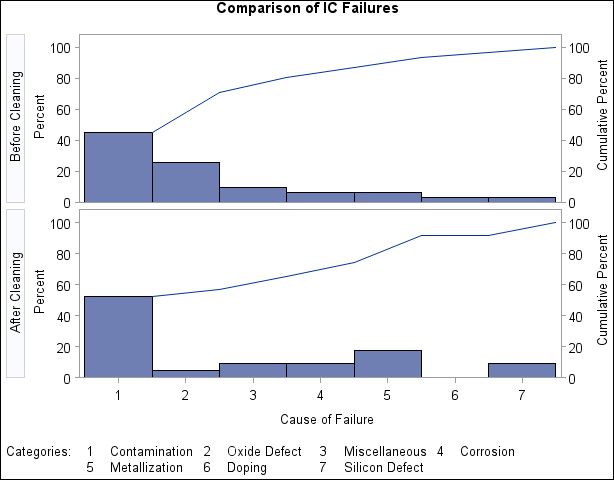
In a comparative Pareto chart, there is always one special cell, called the key cell, in which the bars are displayed in decreasing order, and whose order determines the uniform horizontal axis used for all the
cells. The key cell is positioned at the top of the chart. Here, the key cell is the set of observations for which Stage equals 'Before Cleaning', as specified by the CLASSKEY= option. By default, the levels are sorted in the order determined
by the ORDER1= option, and the key cell is the level that occurs first in this order.
In many applications, it may be more revealing to base comparisons on counts rather than percents. The following statements construct a chart with a frequency scale:
title 'Comparison of IC Failures';
proc pareto data=Failure3;
vbar Cause / class = Stage
freq = Counts
scale = count
intertile = 1.0
nlegend = 'Total Circuits'
classkey = 'Before Cleaning'
cprop;
run;
The chart is shown in Output 15.1.4.
Output 15.1.4: Before-and-After Analysis Using Comparative Pareto Chart
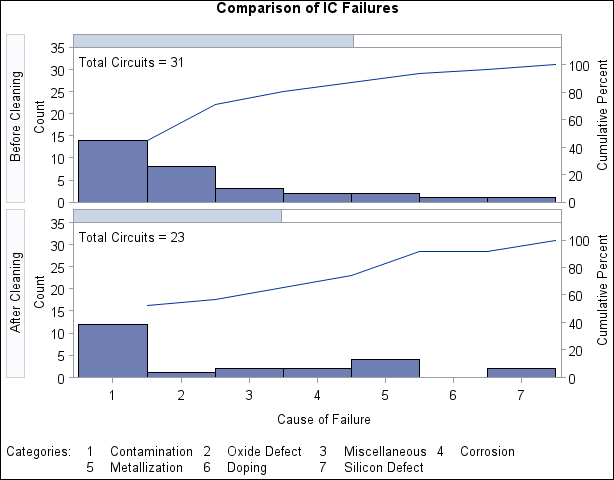
Specifying SCALE=COUNT scales the primary vertical axis in frequency units. The NLEGEND= option adds a sample size legend, and the CFRAMENLEG option frames the legend. The CPROP option adds bars that indicate the proportion of total frequency represented by each cell. The INTERTILE= option separates the tiles with a small offset.
Note that the lower cumulative percent curve in Output 15.1.4 is not anchored to the first bar. This is a consequence of the uniform frequency scale and of the fact that the number of observations in each cell is not the same.