Parameter Estimation and Confidence Intervals
Previous Page|Next Page

The RELIABILITY Procedure

Parameter Estimation and Confidence Intervals

Subsections:

Maximum Likelihood Estimation

Maximum likelihood estimation of the parameters of a statistical model involves maximizing the likelihood or, equivalently, the log likelihood with respect to the parameters. The parameter values at which the maximum occurs are the maximum likelihood estimates of the model parameters. The likelihood is a function of the parameters and of the data.

Let $x_{1}, x_{2}, \ldots , x_{n}$ be the observations in a random sample, including the failures and censoring times (if the data are censored). Let $f(\btheta ;x)$ be the probability density of failure time, $S(\btheta ;x)=Pr\{ X\ge x\} $ be the reliability function, and $F(\btheta ;x)=Pr\{ X\le x\} $ be the cumulative distribution function, where $\btheta $ is the vector of parameters to be estimated, $\btheta =(\theta _{1}, \theta _{2}, \ldots , \theta _{p})$. The probability density, reliability function, and CDF are determined by the specific distribution selected as a model for the data. The log likelihood is defined as

\begin{eqnarray*} \mi {L(\btheta )} & = & \sum _{i}\log (f(\btheta ;x_{i})) + {\sum _{i}}^{}\log (S(\btheta ;x_{i})) + \\ & & {\sum _{i}}^{}\log (F(\btheta ;x_{i})) + {\sum _{i}}^{}[\log (F(\btheta ;x_{ui})-F(\btheta ;x_{li}))] \end{eqnarray*}

where

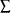  • $\sum $ is the sum over failed units

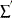  • ${\sum }^{}$ is the sum over right-censored units

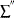  • ${\sum }^{}$ is the sum over left-censored units

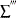  • ${\sum }^{}$ is the sum over interval-censored units

and $(x_{li}, x_{ui})$ is the interval in which the ith unit is interval censored. Only the sums appropriate to the type of censoring in the data are included when the preceding equation is used.

The RELIABILITY procedure maximizes the log likelihood with respect to the parameters $\btheta $ by using a Newton-Raphson algorithm. The Newton-Raphson algorithm is a recursive method for computing the maximum of a function. On the rth iteration, the algorithm updates the parameter vector ${\btheta }_{r}$ with

\[ {\btheta }_{r+1} = {\btheta }_{r} - \mb {H}^{-1}\mb {g} \]

where $\mb {H}$ is the Hessian (second derivative) matrix, and $\mb {g}$ is the gradient (first derivative) vector of the log-likelihood function, both evaluated at the current value of the parameter vector. That is,

\[ \mb {g} = [g_{j}] = \left. \left[ \frac{\partial L}{\partial \theta _{j}}\right] \right|_{\btheta =\btheta _{r}} \]

and

\[ \mb {H} = [{h_{ij}}] = \left. \left[ \frac{\partial ^{2}L}{\partial \theta _{i}\partial \theta _{j}} \right] \right|_{\btheta =\btheta _{r}} \]

Iteration continues until the parameter estimates converge. The convergence criterion is

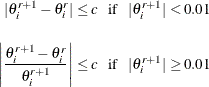
\begin{eqnarray*} |\theta ^{r+1}_{i}-\theta ^{r}_{i}| \leq c \; \; \mbox{ if } \; \; |\theta ^{r+1}_{i}| < 0.01 \\ \nonumber \\ \left| \frac{\theta ^{r+1}_{i}-\theta ^{r}_{i}}{\theta ^{r+1}_{i}}\right| \leq c \; \; \mbox{ if } \; \; |\theta ^{r+1}_{i}| \geq 0.01 \end{eqnarray*}

for all $i=1,2,\ldots ,p$ where c is the convergence criterion. The default value of c is $0.001$, and it can be specified with the CONVERGE= option in the MODEL, PROBPLOT, RELATIONPLOT, and ANALYZE statements.

After convergence by the preceding criterion, the quantity

\[ tc = \frac{\mb {g}\mb {H}^{-1}\mb {g}}{\mi {L}} \]

is computed. If $tc > d$ then a warning is printed that the algorithm did not converge. $tc$ is called the relative Hessian convergence criterion. The default value of d is 0.0001. You can specify other values for d with the CONVH= option. The relative Hessian criterion is useful in detecting the occasional case where no progress can be made in increasing the log likelihood, yet the gradient g is not zero.

A location-scale model has a CDF of the form

\[ F(x) = G\left(\frac{x-\mu }{\sigma }\right) \]

where $\mu $ is the location parameter, $\sigma $ is the scale parameter, and G is a standardized form $(\mu =0, \sigma =1)$ of the cumulative distribution function. The parameter vector is $\btheta $=($\mu $ $\sigma $). It is more convenient computationally to maximize log likelihoods that arise from location-scale models. If you specify a distribution from Table 16.57 that is not a location-scale model, it is transformed to a location-scale model by taking the natural (base e) logarithm of the response. If you specify the lognormal base 10 distribution, the logarithm (base 10) of the response is used. The Weibull, lognormal, and log-logistic distributions in Table 16.57 are not location-scale models. Table 16.58 shows the corresponding location-scale models that result from taking the logarithm of the response.

Maximum likelihood is the default method of estimating the location and scale parameters in the MODEL, PROBPLOT, RELATIONPLOT, and ANALYZE statements. If the Weibull distribution is specified, the logarithms of the responses are used to obtain maximum likelihood estimates ($\hat{\mu }$ $\hat{\sigma }$) of the location and scale parameters of the extreme value distribution. The maximum likelihood estimates ($\hat{\alpha }$, $\hat{\beta }$) of the Weibull scale and shape parameters are computed as $\hat{\alpha }=\exp (\hat{\mu })$ and $\hat{\beta }=1/\hat{\sigma }$.

Maximum likelihood estimates for the Gompertz distributions are obtained by expressing the log-likelihood in terms of $\log (\alpha )$, $\log (\beta )$, and (if applicable) $\log (\theta )$. After the log likelihood is maximized, parameter estimates and their standard errors are transformed from the logarithm metric to the standard metric by using the delta method.

Three-Parameter Weibull

The parameters of the three-parameter Weibull distribution are estimated by maximizing the log likelihood function. The threshold parameter $\theta $ must be less than the minimum failure time $t_0$, unless $\beta =1$, in which case, $\theta $ can be equal to $t_0$. The RELIABILITY procedure sets a default upper bound of $t_0-0.001$ for the threshold in the iterative estimation computations and a default lower bound of 0.0. You can set different bounds by specifying an INEST data set as described in the section INEST Data Set for the Three-Parameter Weibull.

If the shape parameter $\beta $ is less than one, then the density function in Table 16.57 has a singularity at $t=\theta $, and the log likelihood is unbounded above as the threshold parameter approaches the minimum failure time $t_0$. For any fixed $\theta <t_0$, maximum likelihood estimates of the scale and shape parameters $\alpha $ and $\beta $ exist. If $\hat{\beta }<1$ in the iterative estimation procedure, the estimate of the threshold $\theta $ is set to the upper bound and maximum likelihood estimates of $\alpha $ and $\beta $ are computed.

INEST Data Set for the Three-Parameter Weibull

You can specify a SAS data set to set lower bounds, upper bounds, equality constraints, or initial values for estimating the parameters of a three-parameter Weibull distribution by using the INEST= option in the ANALYZE or PROBPLOT statement. The data set must contain a variable named _TYPE_ that specifies the action that you want to take in the iterative estimation process, and some combination of variables named _SCALE_, _SHAPE_, and _THRESHOLD_ that represent the distribution parameters. If BY processing is used, the INEST= data set should also include the BY variables, and there must be at least one observation for each BY group.

The possible values of _TYPE_ and corresponding actions are summarized in Table 16.66.

Table 16.66: _TYPE_ Variable Values

Value of _TYPE_

Action

LB

Lower bound

UB

Upper bound

EQ

Equality

PARMS

Initial value


For example, you can use the INEST data set In created by using the following SAS statements to specify bounds for data that contain the BY variable Group with three BY groups: A, B, and D. The data set In specifies a lower bound for the threshold parameter of –100 for groups A, B, and D, and an upper bound of 3 for the threshold parameter for group D. Since the variables _Scale_ and _Shape_ are set to missing, no action is taken for them, and these variables could be omitted from the data set. 

data In;
   input Group$1 _Type_$ 2-11 _Scale_ _Shape_ _Threshold_;
   datalines;
A    lb    . . -100 
B    lb    . . -100 
D    lb    . . -100 
D    ub    . .  3
;
Regression Models

You can specify a regression model by using the MODEL statement. For example, if you want to relate the lifetimes of electronic parts in a test to Arrhenius-transformed operating temperature, then an appropriate model might be

\[ \mu _{i} = \beta _{0} + x_{i}\beta _{1} \]

where $x_{i}= 1000/(T_{i}+273.15)$, and $T_{i}$ is the centigrade temperature at which the ith unit is tested. Here, $\mb {x}_{i}^\prime = $[ 1 $x_{i}$ ].

There are two types of explanatory variables: continuous variables and classification variables. Continuous variables represent physical quantities, such as temperature or voltage, and they must be numeric. Continuous explanatory variables are sometimes called covariates.

Classification variables identify classification levels and are declared in the CLASS statement. These are also referred to as categorical, dummy, qualitative, discrete, or nominal variables. Classification variables can be either character or numeric. The values of classification variables are called levels. For example, the classification variable Batch could have levels ‘batch1’ and ‘batch2’ to identify items from two production batches. An indicator (0-1) variable is generated for each level of a classification variable and is used as an explanatory variable. See Nelson (1990, p. 277) for an example that uses an indicator variable in the analysis of accelerated life test data. In a model, an explanatory variable that is not declared in a CLASS statement is assumed to be continuous.

By default, all regression models automatically contain an intercept term; that is, the model is of the form

\[ \mu _{i} = \beta _{0} + \beta _{1}x_{i1} + \ldots \]

where $\beta _{0}$ does not have an explanatory variable multiplier. The intercept term can be excluded from the model by specifying INTERCEPT=0 as a MODEL statement option.

For numerical stability, continuous explanatory variables are centered and scaled internally to the procedure. This transforms the parameters $\bbeta $ in the original model to a new set of parameters. The parameter estimates $\bbeta $ and covariances are transformed back to the original scale before reporting, so that the parameters should be interpreted in terms of the originally specified model. Covariates that are indicator variables—that is, those specified in a CLASS statement—are not centered and scaled.

Initial values of the regression parameters used in the Newton-Raphson method are computed by ordinary least squares. The parameters $\bbeta $ and the scale parameter $\sigma $ are jointly estimated by maximum likelihood, taking a logarithmic transformation of the responses, if necessary, to get a location-scale model.

The generalized gamma distribution is fit using log lifetime as the response variable. The regression parameters $\bbeta $, the scale parameter $\sigma $, and the shape parameter $\lambda $ are jointly estimated.

The Weibull distribution shape parameter estimate is computed as $\hat{\beta }=1/\hat{\sigma }$, where $\sigma $ is the scale parameter from the corresponding extreme value distribution. The Weibull scale parameter $\hat{\alpha _{i}}=\exp (\mb {x}^\prime \hat{\bbeta })$ is not computed by the procedure. Instead, the regression parameters $\bbeta $ and the shape $\beta $ are reported.

In a model with one to three continuous explanatory variables x, you can use the RELATION= option in the MODEL statement to specify a transformation that is applied to the variables before model fitting. Table 16.67 shows the available transformations.

Table 16.67: Variable Transformations

Relation

Transformed variable

ARRHENIUS (Nelson parameterization)

$1000/(x+273.15)$

ARRHENIUS2 (activation energy parameterization)

$11605/(x+273.15)$

POWER

$\log (x), \; \; x > 0 $

LINEAR

x

LOGISTIC

$\log \left(\frac{x}{1-x}\right), \; \; 0 < x < 1 $


Nonconstant Scale Parameter

In some situations, it is desirable for the scale parameter to change with the values of explanatory variables. For example, Meeker and Escobar (1998, section 17.5) present an analysis of accelerated life test data where the spread of the data is greater at lower levels of the stress. You can use the LOGSCALE statement to specify the scale parameter as a function of explanatory variables. You must also have a MODEL statement to specify the location parameter. Explanatory variables can be continuous variables, indicator variables specified in the CLASS statement, or any interaction combination. The variables can be the same as specified in the MODEL statement, or they can be different variables. Any transformation specified with the RELATION= MODEL statement option will be applied to the same variable appearing in the LOGSCALE statement. See the section Regression Model with Nonconstant Scale for an example of fitting a model with nonconstant scale parameter.

The form of the model for the scale parameter is

\[ \log (\sigma _ i) = \beta _{0} + \beta _{1}x_{i1} + \ldots +\beta _{p}x_{ip} \]

where $\beta _{0}$ is the intercept term. The intercept term can be excluded from the model by specifying INTERCEPT=0 as a LOGSCALE statement option.

The parameters $\beta _{0}, \beta _{1}, \ldots , \beta _{p}$ are estimated by maximum likelihood jointly with all the other parameters in the model.

Stable Parameters

The location and scale parameters $(\mu , \sigma )$ are estimated by maximizing the likelihood function by numerical methods, as described previously. An alternative parameterization that is likely to have better numerical properties for heavy censoring is $(\eta , \sigma )$, where $\eta = \mu + z_{p}\sigma $ and $z_{p}$ is the pth quantile of the standardized distribution. See Meeker and Escobar (1998, p. 90) and Doganaksoy and Schmee (1993) for more details on alternate parameterizations.

By default, RELIABILITY estimates a value of $z_{p}$ from the data that will improve the numerical properties of the estimation. You can also specify values of p from which the value of $z_{p}$ will be computed with the PSTABLE= option in the ANALYZE, PROBPLOT, RELATIONPLOT, or MODEL statement. Note that a value of p = 0.632 for the Weibull and extreme value and p = 0.5 for all other distributions will give $z_{p}=0$ and the parameterization will then be the usual location-scale parameterization.

All estimates and related statistics are reported in terms of the location and scale parameters $(\mu , \sigma )$. If you specify the ITPRINT option in the ANALYZE, PROBPLOT, or RELATIONPLOT statement, a table showing the values of p, $\nu $, $\sigma $, and the last evaluation of the gradient and Hessian for these parameters is produced.

Covariance Matrix

An estimate of the covariance matrix of the maximum likelihood estimators (MLEs) of the parameters $\btheta $ is given by the inverse of the negative of the matrix of second derivatives of the log likelihood, evaluated at the final parameter estimates:

\[ \bSigma = [\sigma _{ij}] = -\mb {H}^{-1} = -\left[ \frac{\partial ^{2}L}{\partial \theta _{i}\partial \theta _{j}} \right]^{-1}_{\btheta =\hat{\btheta }} \]

The negative of the matrix of second derivatives is called the observed Fisher information matrix. The diagonal term $\sigma _{ii}$ is an estimate of the variance of $\hat{\theta }_{i}$. Estimates of standard errors of the MLEs are provided by

\[ \mr {SE}_{\theta _{i}} = \sqrt {\sigma _{ii}} \]

An estimator of the correlation matrix is

\[ \mb {R} = \left[ \frac{\sigma _{ij}}{\sqrt {\sigma _{ii}\sigma _{jj}}} \right] \]

The covariance matrix for the Weibull distribution parameter estimators is computed by a first-order approximation from the covariance matrix of the estimators of the corresponding extreme value parameters $(\mu , \sigma )$ as

\begin{eqnarray*} \textrm{Var}(\hat{\alpha }) & = & [\exp (\hat{\mu })]^{2}\textrm{Var}(\hat{\mu }) \\ \textrm{Var}(\hat{\beta }) & = & \frac{\textrm{Var}(\hat{\sigma })}{\hat{\sigma }^{4}} \\ \textrm{Cov}(\hat{\alpha },\hat{\beta }) & = & -\frac{\exp (\hat{\mu )}}{\hat{\sigma }^{2}}\textrm{Cov}(\hat{\mu },\hat{\sigma }) \end{eqnarray*}

For the regression model, the variance of the Weibull shape parameter estimator $\hat{\beta }$ is computed from the variance of the estimator of the extreme value scale parameter $\sigma $ as shown previously. The covariance of the regression parameter estimator $\hat{\beta }_{i}$ and the Weibull shape parameter estimator $\hat{\beta }$ is computed in terms of the covariance between $\hat{\beta }_{i}$ and $\hat{\sigma }$ as

\[ \mr {Cov}(\hat{\beta }_{i}, \hat{\beta }) = -\frac{\mr {Cov}(\hat{\beta _{i}},\hat{\sigma })}{\hat{\sigma }^{2}} \]
Confidence Intervals for Distribution Parameters

Table 16.68 shows the method of computation of approximate two-sided $\gamma \times 100\% $ confidence limits for distribution parameters. The default value of confidence is $\gamma = 0.95$. Other values of confidence are specified using the CONFIDENCE= option. In Table 16.68, $K_{\gamma }$ represents the $(1+\gamma )/2 \times 100\% $ percentile of the standard normal distribution, and $\hat{\mu }$ and $\hat{\sigma }$ are the MLEs of the location and scale parameters for the normal, extreme value, and logistic distributions. For the lognormal, Weibull, and log-logistic distributions, $\hat{\mu }$ and $\hat{\sigma }$ represent the MLEs of the corresponding location and scale parameters of the location-scale distribution that results when the logarithm of the lifetime is used as the response. For the Weibull distribution, $\mu $ and $\sigma $ are the location and scale parameters of the extreme value distribution for the logarithm of the lifetime. $\mr {SE}_{\hat{\theta }}$ denotes the standard error of the MLE of $\theta $, computed as the square root of the appropriate diagonal element of the inverse of the Fisher information matrix.

For the Gompertz distributions, estimation of all parameters takes place in the logarithm metric. For example, a confidence interval for the logarithm of scale is computed as $\log (\hat\alpha ) \pm K_\gamma \mr {SE}_{\log (\hat\alpha )}$. The confidence interval in the standard metric is then obtained by taking $e$ to the power equal to each endpoint.

Table 16.68: Confidence Limit Computation

 

Parameters

Distribution

Location $\mu $ or

Scale

Shape

 

Threshold $\theta $

   

Normal

$\mu _{L}=\hat{\mu }-K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{L}=\hat{\sigma }/\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  
 

$\mu _{U}=\hat{\mu }+K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{U}=\hat{\sigma }\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  

Lognormal

$\mu _{L}=\hat{\mu }-K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{L}=\hat{\sigma }/\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  
 

$\mu _{U}=\hat{\mu }+K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{U}=\hat{\sigma }\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  

Lognormal

$\mu _{L}=\hat{\mu }-K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{L}=\hat{\sigma }/\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  

(base 10)

$\mu _{U}=\hat{\mu }+K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{U}=\hat{\sigma }\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  

Extreme value

$\mu _{L}=\hat{\mu }-K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{L}=\hat{\sigma }/\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  
 

$\mu _{U}=\hat{\mu }+K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{U}=\hat{\sigma }\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  

Weibull

 

$\alpha _{L}=\exp [\hat{\mu }-K_{\gamma }\mr {(SE}_{\hat{\mu }})]$

$\beta _{L}=\exp [-K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]/\hat{\sigma }$

   

$\alpha _{U}=\exp [\hat{\mu }+K_{\gamma }\mr {(SE}_{\hat{\mu }})]$

$\beta _{U}=\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]/\hat{\sigma }$

Exponential

 

$\alpha _{L}=\exp [\hat{\mu }-K_{\gamma }\mr {(SE}_{\hat{\mu }})]$

$ $

   

$\alpha _{U}=\exp [\hat{\mu }+K_{\gamma }\mr {(SE}_{\hat{\mu }})]$

$ $

Logistic

$\mu _{L}=\hat{\mu }-K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{L}=\hat{\sigma }/\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  
 

$\mu _{U}=\hat{\mu }+K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{U}=\hat{\sigma }\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  

Log-logistic

$\mu _{L}=\hat{\mu }-K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{L}=\hat{\sigma }/\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  
 

$\mu _{U}=\hat{\mu }+K_{\gamma }\mr {(SE}_{\hat{\mu }})$

$\sigma _{U}=\hat{\sigma }\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

  

Generalized

 

$\sigma _{L}=\hat{\sigma }/\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

$\mu _{L}=\hat{\lambda }-K_{\gamma }\mr {(SE}_{\hat{\lambda }})$

Gamma

 

$\sigma _{U}=\hat{\sigma }\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]$

$\mu _{U}=\hat{\lambda }+K_{\gamma }\mr {(SE}_{\hat{\lambda }})$

Three-parameter

$\theta _{L}=\hat{\theta }-K_{\gamma }\mr {(SE}_{\hat{\theta }})$

$\alpha _{L}=\exp [\hat{\mu }-K_{\gamma }\mr {(SE}_{\hat{\mu }})]$

$\beta _{L}=\exp [-K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]/\hat{\sigma }$

Weibull

$\theta _{U}=\hat{\theta }+K_{\gamma }\mr {(SE}_{\hat{\theta }})$

$\alpha _{U}=\exp [\hat{\mu }+K_{\gamma }\mr {(SE}_{\hat{\mu }})]$

$\beta _{U}=\exp [K_{\gamma }\mr {(SE}_{\hat{\sigma }})/\hat{\sigma }]/\hat{\sigma }$


Regression Parameters

Approximate $\gamma \times 100\% $ confidence limits for the regression parameter $\beta _{i}$ are given by

\[ \beta _{iL}=\hat{\beta }_{i} - K_{\gamma }(\mr {SE}_{\hat{\beta }_{i}}) \]
\[ \beta _{iU}=\hat{\beta }_{i} + K_{\gamma }(\mr {SE}_{\hat{\beta }_{i}}) \]
Percentiles

The maximum likelihood estimate of the $p \times 100\% $ percentile $x_{p}$ for the extreme value, normal, and logistic distributions is given by

\[ \hat{x}_{p} = \hat{\mu } + z_{p}\hat{\sigma } \]

where $z_{p}=G^{-1}(p)$, G is the standardized CDF shown in Table 16.69, and $(\hat{\mu },\hat{\sigma })$ are the maximum likelihood estimates of the location and scale parameters of the distribution. The maximum likelihood estimate of the percentile $t_{p}$ for the Weibull, lognormal, and log-logistic distributions is given by

\[ \hat{t}_{p} = \exp [\hat{\mu } + z_{p}\hat{\sigma }] \]

where $z_{p}=G^{-1}(p)$, and G is the standardized CDF of the location-scale model corresponding to the logarithm of the response. For the lognormal (base 10) distribution,

\[ \hat{t}_{p} = 10^{[\hat{\mu } + z_{p}\hat{\sigma }]} \]

The maximum likelihood estimate of the percentile $t_{p}$ for the three-parameter Weibull distribution is computed by

\[ \hat{t}_{p} = \hat{\theta } + \exp [\hat{\mu } + z_{p}\hat{\sigma }] \]

where $z_{p}=G^{-1}(p)$, and G is the standardized CDF of extreme value distribution.

The maximum likelihood estimate of the percentile $t_ p$ for the standard Gompertz distribution is computed by

\[ \hat{t}_ p = \hat{\alpha } \log \{ 1 - \hat\beta ^{-1}\log (1-p)\} \]

Because the quantile function depends on Lambert’s $W$ function and has no closed form, the percentile for the three-parameter Gompertz distribution is obtained by using a bisection algorithm to solve the following equation:

\[ p = F(\hat{t}_ p) = 1 - \exp \left\{ \hat\beta - \frac{\hat\theta \hat{t}_ p}{\hat\alpha } - \hat\beta \exp \left(\frac{\hat{t}_ p}{\hat\alpha }\right) \right\} \]

Table 16.69: Standardized Cumulative Distribution Functions

 

Location-Scale

Location-Scale

Distribution

Distribution

CDF

Weibull

Extreme value

$1 - \exp [-\exp (z)]$

Lognormal

Normal

$\int _{-\infty }^{z}\frac{1}{\sqrt {2\pi }}\exp \left(-\frac{u^{2}}{2}\right)du $

Log-logistic

Logistic

$\frac{\exp (z)}{1+\exp (z)}$


Confidence Intervals

The variance of the MLE of the $p\times 100\% $ percentile for the normal, extreme value, or logistic distribution is

\[ \mr {Var}(\hat{x}_{p}) = \mr {Var}(\hat{\mu }) + z_{p}^{2}\mr {Var}(\hat{\sigma }) + 2z_{p}\mr {Cov}(\hat{\mu },\hat{\sigma }) \]

Two-sided approximate $100\gamma \% $ confidence limits for $x_{p}$ are

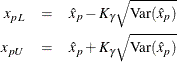
\begin{eqnarray*} x_{pL} & = & \hat{x}_{p} - K_{\gamma }\sqrt {\textrm{Var}(\hat{x}_{p})} \\ x_{pU} & = & \hat{x}_{p} + K_{\gamma }\sqrt {\textrm{Var}(\hat{x}_{p})} \end{eqnarray*}

where $K_{\gamma }$ represents the $100(1+\gamma )/2 \times 100\% $ percentile of the standard normal distribution.

The limits for the lognormal, Weibull, or log-logistic distributions are

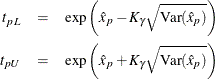
\begin{eqnarray*} {t}_{pL} & = & \exp \left(\hat{x}_{p} - K_{\gamma }\sqrt {\textrm{Var}(\hat{x}_{p})}\right) \\ {t}_{pU} & = & \exp \left(\hat{x}_{p} + K_{\gamma }\sqrt {\textrm{Var}(\hat{x}_{p})}\right) \end{eqnarray*}

where $x_{p}$ refers to the percentile of the corresponding location-scale distribution (normal, extreme value, or logistic) for the logarithm of the lifetime. For the lognormal (base 10) distribution,

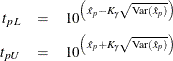
\begin{eqnarray*} {t}_{pL} & = & 10^{\left(\hat{x}_{p} - K_{\gamma }\sqrt {\textrm{Var}(\hat{x}_{p})}\right)} \\ {t}_{pU} & = & 10^{\left(\hat{x}_{p} + K_{\gamma }\sqrt {\textrm{Var}(\hat{x}_{p})}\right)} \end{eqnarray*}

Approximate limits for the three-parameter Weibull distribution are computed as

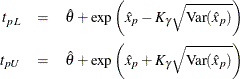
\begin{eqnarray*} {t}_{pL} & = & \hat{\theta }+\exp \left(\hat{x}_{p} - K_{\gamma }\sqrt {\textrm{Var}(\hat{x}_{p})}\right) \\ {t}_{pU} & = & \hat{\theta }+\exp \left(\hat{x}_{p} + K_{\gamma }\sqrt {\textrm{Var}(\hat{x}_{p})}\right) \end{eqnarray*}

where $x_{p}$ refers to the percentile of the standard extreme value distribution.

For the Gompertz distributions, confidence limits are computed as

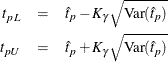
\begin{eqnarray*} {t}_{pL} & = & \hat{t}_ p - K_\gamma \sqrt {\textrm{Var}(\hat{t}_ p)} \\ {t}_{pU} & = & \hat{t}_ p + K_\gamma \sqrt {\textrm{Var}(\hat{t}_ p)} \end{eqnarray*}

where $\textrm{Var}(\hat{t}_ p)$ is calculated by the delta method. Because the quantile function has no closed form, the derivatives that are required for the three-parameter Gompertz distribution are obtained by the numerical method of finite differencing.

Reliability Function

For the extreme value, normal, and logistic distributions shown in Table 16.69, the maximum likelihood estimate of the reliability function $R(x) = \mr {Pr}\{ X>x\} $ is given by

\[ \hat{R}(x)=1-F\left(\frac{x-\hat{\mu }}{\hat{\sigma }}\right) \]

For the Gompertz distributions, the MLE of the reliability function is

\[ \hat{R}(x) = \exp \left\{ \hat\beta - \frac{\hat\theta x}{\hat\alpha } - \hat\beta \exp \left(\frac{x}{\hat\alpha }\right) \right\} \]

where $\hat\theta = 0$ for the standard, two-parameter Gompertz distribution.

The MLE of the CDF is $\hat{F}(x)=1-\hat{R}(x)$.

Confidence Intervals

Let $\hat{u}=\frac{x-\hat{\mu }}{\hat{\sigma }}$. The approximate variance of u is

\[ \mr {Var}(\hat{u})\approx \frac{\mr {Var}(\hat{\mu })+\hat{u}^{2}\mr {Var}(\hat{\sigma })+ 2\hat{u}\mr {Cov}(\hat{\mu },\hat{\sigma })}{\hat{\sigma }^{2}} \]

Two-sided approximate $\gamma \times 100\% $ confidence intervals for $R(x)$ are computed as

\[ R_{L}(x)=\hat{R}(u_{2}) \]
\[ R_{U}(x)=\hat{R}(u_{1}) \]

where

\[ u_{1}=\hat{u} - K_{\gamma }\sqrt {\mr {Var}(\hat{u})} \]
\[ u_{2}=\hat{u} + K_{\gamma }\sqrt {\mr {Var}(\hat{u})} \]

and $K_{\gamma }$ represents the $(1+\gamma )/2 \times 100\% $ percentile of the standard normal distribution. The corresponding limits for the CDF are

\[ F_{L}(x) = 1-R_{U}(x) \]
\[ F_{U}(x) = 1-R_{L}(x) \]

For the Gompertz distributions, confidence intervals for $R(x)$ are computed as

\[ R_{L}(x) = \exp \{ -\exp (u_2)\} \]
\[ R_{U}(x) = \exp \{ -\exp (u_1)\} \]

where $\hat{u} = \log [-\log \{ \hat{R}_ G(x)\} ]$, $R_ G(x)$ is the Gompertz reliability function, and

\[ u_{1}=\hat{u} - K_{\gamma }\sqrt {\mr {Var}(\hat{u})} \]
\[ u_{2}=\hat{u} + K_{\gamma }\sqrt {\mr {Var}(\hat{u})} \]

The variance term $\mr {Var}(\hat{u})$ is obtained by the delta method from the covariance matrix of the original parameter estimates.

As an alternative, you can request that two-sided $\gamma \times 100\% $ likelihood ratio confidence limits for the reliability function and the CDF be computed by specifying the LRCLSURV option in the ANALYZE statement or the LRCLSURV option in the PROBPLOT statement.

Limits for the Weibull, lognormal, and log-logistic reliability function $R(t)$ are the same as those for the corresponding extreme value, normal, or logistic reliability $R(y)$, where $y=\log (t)$. Limits for the three-parameter Weibull use $y=\log (t-\hat{\theta })$ and the extreme value CDF.

You can create a table containing estimates of the reliability function, the CDF, and confidence limits computed as described in this section with the SURVTIME= option in the ANALYZE statement or with the SURVTIME= option in the PROBPLOT statement. You can plot confidence limits for the CDF on probability plots created with the PROBPLOT statement with the PINTERVALS=CDF option in the PROBPLOT statement. PINTERVALS=CDF is the default option for parametric confidence limits on probability plots.

Estimation with the Binomial and Poisson Distributions

In addition to estimating the parameters of the distributions in Table 16.57, you can estimate parameters, compute confidence limits, compute predicted values and prediction limits, and compute chi-square tests for differences in groups for the binomial and Poisson distributions by using the ANALYZE statement. Specify either BINOMIAL or POISSON in the DISTRIBUTION statement to use one of these distributions. The ANALYZE statement options available for the binomial and Poisson distributions are given in Table 16.5. See the section Analysis of Binomial Data for an example of an analysis of binomial data.

Binomial Distribution

If r is the number of successes and n is the number of trials in a binomial experiment, then the maximum likelihood estimator of the probability p in the binomial distribution in Table 16.59 is computed as

\[ \hat{p} = r/n \]

Two-sided $\gamma \times 100\% $ confidence limits for p are computed as in Johnson, Kotz, and Kemp (1992, p. 130):

\[ p_{L}= \frac{\nu _{1}F[(1-\gamma )/2; \nu {_1}, \nu _{2}] }{\nu _{2} + \nu _{1}F[(1-\gamma )/2; \nu {_1}, \nu _{2}] } \]

with $\nu _{1}=2r$ and $\nu _{2}=2(n-r+1)$ and

\[ p_{U}= \frac{\nu _{1}F[(1+\gamma )/2; \nu {_1}, \nu _{2}] }{\nu _{2} + \nu _{1}F[(1+\gamma )/2; \nu {_1}, \nu _{2}] } \]

with $\nu _{1}=2(r+1)$ and $\nu _{2}=2(n-r)$, where $F[\gamma ;\nu _{1},\nu _{2}]$ is the $\gamma \times 100\% $ percentile of the F distribution with $\nu _{1}$ degrees of freedom in the numerator and $\nu _{2}$ degrees of freedom in the denominator.

You can compute a sample size required to estimate p within a specified tolerance w with probability $\gamma $. Nelson (1982, p. 206) gives the following formula for the approximate sample size:

\[ n \approx \hat{p}(1-\hat{p})\left(\frac{K_{\gamma }}{w}\right)^{2} \]

where $K_{\gamma }$ is the $(1+\gamma )/2 \times 100\% $ percentile of the standard normal distribution. The formula is based on the normal approximation for the distribution of $\hat{p}$. Nelson recommends using this formula if $np > 10$ and $np(1-p) > 10$. The value of $\gamma $ used for computing confidence limits is used in the sample size computation. The default value of confidence is $\gamma = 0.95$. Other values of confidence are specified using the CONFIDENCE= option. You specify a tolerance of number with the TOLERANCE(number) option.

The predicted number of successes X in a future sample of size m, based on the previous estimate of p, is computed as

\[ \hat{X}=m(r/n) = m\hat{p} \]

Two-sided approximate $\gamma \times 100)\% $ prediction limits are computed as in Nelson (1982, p. 208). The prediction limits are the solutions $X_{L}$ and $X_{U}$ of

\[ X_{U}/m = [(r+1)/n]F[(1+\gamma )/2;2(r+1),2X_{U}] \]
\[ m/(X_{L}+1)=(n/r)F[(1+\gamma )/2;2(X_{L}+1),2r] \]

where $F[\gamma ;\nu _{1},\nu _{2}]$ is the $\gamma \times 100$% percentile of the F distribution with $\nu _{1}$ degrees of freedom in the numerator and $\nu _{2}$ degrees of freedom in the denominator. You request predicted values and prediction limits for a future sample of size number with the PREDICT(number) option.

You can test groups of binomial data for equality of their binomial probability by using the ANALYZE statement. You specify the K groups to be compared with a group variable having K levels.

Nelson (1982, p. 450) discusses a chi-square test statistic for comparing K binomial proportions for equality. Suppose there are $r_{i}$ successes in $n_{i}$ trials for $i=1,2, \ldots , K$. The grouped estimate of the binomial probability is

\[ \hat{p}=\frac{r_{1}+r_{2}+\cdots +r_{K}}{n_{1}+n_{2}+\cdots +n_{K}} \]

The chi-square test statistic for testing the hypothesis $p_{1}=p_{2}=\ldots =p_{K}$ against $p_{i}\neq p_{j}$ for some i and j is

\[ Q=\sum _{i=1}^{K}\frac{(r_{i}-n_{i}\hat{p})^{2}}{n_{i}\hat{p}(1-\hat{p})} \]

The statistic Q has an asymptotic chi-square distribution with K – 1 degrees of freedom. The RELIABILITY procedure computes the contribution of each group to Q, the value of Q, and the p-value for Q based on the limiting chi-square distribution with K – 1 degrees of freedom. If you specify the PREDICT option, predicted values and prediction limits are computed for each group, as well as for the pooled group. The p-value is defined as $p_{0}=1-\chi ^{2}_{K-1}[Q]$, where $\chi ^{2}_{K-1}[x]$ is the chi-square CDF with K – 1 degrees of freedom, and Q is the observed value. A test of the hypothesis of equal binomial probabilities among the groups with significance level $\alpha $ is

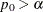  • $p_{0} > \alpha $ : do not reject the equality hypothesis

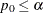  • $p_{0} \le \alpha $ : reject the equality hypothesis

Poisson Distribution

You can use the ANALYZE statement to model data by using the Poisson distribution. The data consist of a count Y of occurrences in a “length” of observation T. Observation T is typically an exposure time, but it can have other units, such as distance. The ANALYZE statement enables you to compute the rate of occurrences, confidence limits, and prediction limits.

An estimate of the rate $\lambda $ is computed as

\[ \hat{\lambda }=Y/T \]

Two-sided $\gamma \times 100\% $ confidence limits for $\lambda $ are computed as in Nelson (1982, p. 201):

\[ \lambda _{L}=0.5\chi ^{2}[(1-\gamma )/2;2Y]/T \]
\[ \lambda _{U}=0.5\chi ^{2}[(1+\gamma )/2;2(Y+1)]/T \]

where $\chi ^{2}[\delta ;\nu ]$ is the $\delta \times 100\% $ percentile of the chi-square distribution with $\nu $ degrees of freedom.

You can compute a length T required to estimate $\lambda $ within a specified tolerance w with probability $\gamma $. Nelson (1982, p. 202) provides the following approximate formula:

\[ \hat{T}\approx \hat{\lambda }\left(\frac{K_{\gamma }}{w}\right)^{2} \]

where $K_{\gamma }$ is the $(1+\gamma )/2 \times 100\% $ percentile of the standard normal distribution. The formula is based on the normal approximation for $\hat{\lambda }$ and is more accurate for larger values of $\lambda T$. Nelson recommends using the formula when $\lambda T > 10$. The value of $\gamma $ used for computing confidence limits is also used in the length computation. The default value of confidence is $\gamma = 0.95$. Other values of confidence are specified using the CONFIDENCE= option. You specify a tolerance of number with the TOLERANCE(number) option.

The predicted future number of occurrences in a length S is

\[ \hat{X}=(Y/T)S = \hat{\lambda }S \]

Two-sided approximate $\gamma \times 100\% $ prediction limits are computed as in Nelson (1982, p. 203). The prediction limits are the solutions $X_{L}$ and $X_{U}$ of

\[ X_{U}/S = [(Y+1)/T]F[(1+\gamma )/2;2(Y+1),2X_{U}] \]
\[ S/(X_{L}+1)=(T/Y)F[(1+\gamma )/2;2(X_{L}+1),2Y] \]

where $F[\gamma ;\nu _{1},\nu _{2}]$ is the $\gamma \times 100\% $ percentile of the F distribution with $\nu _{1}$ degrees of freedom in the numerator and $\nu _{2}$ degrees of freedom in the denominator. You request predicted values and prediction limits for a future exposure number with the PREDICT(number) option.

You can compute a chi-square test statistic for comparing K Poisson rates for equality. You specify the K groups to be compared with a group variable having K levels.

See Nelson (1982, p. 444) for more information. Suppose that there are $Y_{i}$ Poisson counts in lengths $T_{i}$ for $i=1,2, \ldots , K$ and that the $Y_{i}$ are independent. The grouped estimate of the Poisson rate is

\[ \hat{\lambda }=\frac{Y_{1}+Y_{2}+\cdots +Y_{K}}{T_{1}+T_{2}+\cdots +T_{K}} \]

The chi-square test statistic for testing the hypothesis $\lambda _{1}=\lambda _{2}=\ldots =\lambda _{K}$ against $\lambda _{i}\neq \lambda _{j}$ for some i and j is

\[ Q=\sum _{i=1}^{K}\frac{(Y_{i}-\hat{\lambda }T_{i})^{2}}{\hat{\lambda }T_{i}} \]

The statistic Q has an asymptotic chi-square distribution with K – 1 degrees of freedom. The RELIABILITY procedure computes the contribution of each group to Q, the value of Q, and the p-value for Q based on the limiting chi-square distribution with K – 1 degrees of freedom. If you specify the PREDICT option, predicted values and prediction limits are computed for each group, as well as for the pooled group. The p-value is defined as $p_{0}=1-\chi ^{2}_{K-1}[Q]$, where $\chi ^{2}_{K-1}[x]$ is the chi-square CDF with K – 1 degrees of freedom and Q is the observed value. A test of the hypothesis of equal Poisson rates among the groups with significance level $\alpha $ is

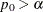  • $p_{0} > \alpha $ : accept the equality hypothesis

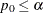  • $p_{0} \le \alpha $ : reject the equality hypothesis

Least Squares Fit to the Probability Plot

Fitting to the probability plot by least squares is an alternative to maximum likelihood estimation of the parameters of a life distribution. Only the failure times are used. A least squares fit is computed using points $(x_{(i)}, m_{i})$, where $m_{i}=F^{-1}(a_{i})$ and $a_{i}$ are the plotting positions as defined in the section Probability Plotting. The $x_{i}$ are either the lifetimes for the normal, extreme value, or logistic distributions or the log lifetimes for the lognormal, Weibull, or log-logistic distributions. The ANALYZE, PROBPLOT, or RELATIONPLOT statement option FITTYPE=LSXY specifies the $x_{(i)}$ as the dependent variable (’y-coordinate’) and the $m_{i}$ as the independent variable (’x-coordinate’). You can optionally reverse the quantities used as dependent and independent variables by specifying the FITTYPE=LSYX option.

Weibayes Estimation

Weibayes estimation is a method of performing a Weibull analysis when there are few or no failures. The FITTYPE=WEIBAYES option requests this method. The method of Nelson (1985) is used to compute a one-sided confidence interval for the Weibull scale parameter when the Weibull shape parameter is specified. See Abernethy (2006) for more discussion and examples. The Weibull shape parameter $\beta $ is assumed to be known and is specified to the procedure with the SHAPE=number option. Let $T_{1},T_{2},\ldots ,T_{n}$ be the failure and censoring times, and let $r\ge 0$ be the number of failures in the data. If there are no failures $(r=0)$, a lower $\gamma \times 100\% $ confidence limit for the Weibull scale parameter $\alpha $ is computed as

\[ \alpha _{L}=\{ \sum _{i=1}^{n}T_{i}^{\beta }/[-\log (1-\gamma )]\} ^{1/\beta } \]

The default value of confidence is $\gamma = 0.95$. Other values of confidence are specified using the CONFIDENCE= option.

If $r\ge 1$, the MLE of $\alpha $ is given by

\[ \hat{\alpha }=[\sum _{i=1}^{n}T_{i}^{\beta }/r]^{1/\beta } \]

and a lower $\gamma \times 100\% $ confidence limit for the Weibull scale parameter $\alpha $ is computed as

\[ \alpha _{L}=\hat{\alpha }[2r/\chi ^2(\gamma , 2r+2)]^{1/\beta } \]

where $\chi ^2(\gamma , 2r+2)$ is the $\gamma $ percentile of a chi-square distribution with $2r+2$ degrees of freedom. The procedure uses the specified value of $\beta $ and the computed value of $\alpha _{L}$ to compute distribution percentiles and the reliability function.

Estimation With Multiple Failure Modes

In many applications, units can experience multiple causes of failure, or failure modes. For example, in the section Weibull Probability Plot for Two Combined Failure Modes, insulation specimens can experience either early failures due to manufacturing defects or degradation failures due to aging. The FMODE statement is used to analyze this type of data. See the section FMODE Statement for the syntax of the FMODE statement. This section describes the analysis of data when units experience multiple failure modes.

The assumptions used in the analysis are

  • a cause, or mode, can be identified for each failure

  • failure modes follow a series-system model; i.e., a unit fails when a failure due to one of the modes occurs

  • each failure mode has the specified lifetime distribution with different parameters

  • failure modes act statistically independently

Suppose there are m failure modes, with lifetime distribution functions $F_{1}(t), F_{2}(t), \ldots , F_{m}(t)$.

If you wish to estimate the lifetime distribution of a failure mode, say mode i, acting alone, specify the KEEP keyword in the FMODE statement. The failures from all other modes are treated as right-censored observations, and the lifetime distribution is estimated by one of the methods described in other sections, such as maximum likelihood. This lifetime distribution is interpreted as the distribution if the specified failure mode is acting alone, with all other modes eliminated. You can also specify more than one mode to KEEP, but the assumption is that all the specified modes have the same distribution.

If you specify the ELIMINATE keyword, failures due to the specified modes are treated as right censored. The resulting distribution estimate is the failure distribution if the specified modes are eliminated.

If you specify the COMBINE keyword, the failure distribution when all the modes specified in the FMODE statement modes act is estimated. The failure distribution $F_{i}(t), i = 1, 2, \ldots , m$, from each individual mode is first estimated by treating all failures from other modes as right censored. The estimated failure distributions are then combined to get an estimate of the lifetime distribution when all modes act,

\[ \hat{F}(t) = 1 - \prod _{i=1}^{m}[1 - \hat{F}_{i}(t)] \]

Pointwise approximate asymptotic normal confidence limits for $F(t)$ can be obtained by the delta method. See Meeker and Escobar (1998, appendix B.2). The delta method variance of $\hat{F}(t)$ is, assuming independence of failure modes,

\[ \mr {Var}(\hat{F}(t)) = \sum _{i=1}^{m}[S_{0}(u_1)S_{0}(u_2)\ldots f_{0}(u_ i)\ldots S_{0}(u_ m)]^2 \mr {Var}(u_ i) \]

where $u_ i = \frac{y - \hat{\mu }_ i}{\hat{\sigma }_ i}$, y is t for the extreme value, normal, and logistic distributions or $\log (t)$ for the Weibull, lognormal or log-logistic distributions, $\hat{\mu }_ i$ and $\hat{\sigma }_ i$ are location and scale parameter estimates for mode i, and $S_0$ and $f_0$ are the standard ($\mu =0, \sigma =1$) survival function and density function for the specified distribution.

Two-sided approximate $(1-\alpha )100\% $ pointwise confidence intervals are computed as in Meeker and Escobar (1998, section 3.6) as

\[ [ F_ L, F_ U ] = \left[ \frac{\hat{F}}{\hat{F} + ( 1-\hat{F})w}, \; \; \frac{\hat{F}}{\hat{F} + ( 1-\hat{F})/w} \right] \]

where

\[ w = \exp \left[\frac{z_{1-\alpha /2}\mbox{se}_{\hat{F}}}{(\hat{F}(1-\hat{F}))} \right] \]

where $ \mbox{se}_{\hat{F}} = \sqrt {\mr {Var}(\hat{F}(t))} $ and $z_ p$ is the pth quantile of the standard normal distribution.

Previous Page|Next Page|Top of Page
Copyright © SAS Institute Inc. All Rights Reserved.