The RELIABILITY Procedure

Analysis of Interval Age Recurrence Data

You can analyze recurrence data when the recurrence ages are grouped into intervals, instead of being exact ages. Figure 16.41 shows a listing of a SAS data set containing field data on replacements of defrost controls in 22,914 refrigerators, whose ages are grouped by months in service. Nelson (2002, problem 5.2, chapter 5) presents these data. Grouping the control data on the 22,914 refrigerators into age intervals enables you to represent the data by 29 data records, instead of requiring a single data record for each refrigerator, as required for exact recurrence data.

The variables Lower and Upper are the lower and upper monthly interval endpoints, Recurrences is the number of defrost control replacements in each month, and Censored is the number of refrigerator histories censored in each month—that is, the number with current age in the monthly interval. Data are entered as shown in Figure 16.41.

Figure 16.41: Listing of the Defrost Controls Data

Obs	Lower	Upper	Recurrences	Censored
1	0	1	83	0
2	1	2	35	0
3	2	3	23	0
4	3	4	15	0
5	4	5	22	0
6	5	6	16	3
7	6	7	13	36
8	7	8	12	24
9	8	9	15	29
10	9	10	15	37
11	10	11	24	40
12	11	12	12	20041
13	12	13	7	14
14	13	14	11	17
15	14	15	15	13
16	15	16	6	28
17	16	17	8	22
18	17	18	9	27
19	18	19	9	64
20	19	20	5	94
21	20	21	6	119
22	21	22	6	118
23	22	23	6	138
24	23	24	5	1188
25	24	25	7	17
26	25	26	5	28
27	26	27	5	99
28	27	28	6	128
29	28	29	3	590

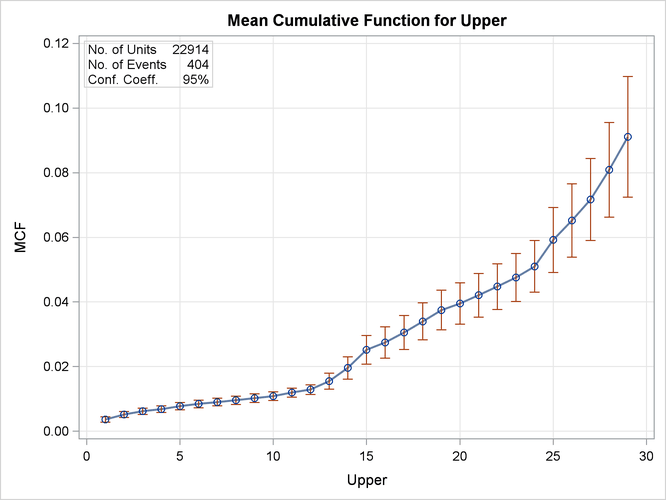
The following SAS statements create the plot of the sample MCF of defrost control replacement shown in Figure 16.42 and the tabular listing in Figure 16.43:

proc reliability data=defrost;
   mcfplot ( interval    = Lower Upper
             recurrences = Recurrences
             censor      = Censored ) / plotsymbol = X
                                        vaxis = 0 to .12 by .04
                                        interpolate = join;
run;

Pointwise confidence limits are included on the plot and in the tabular listing. These limits are approximate, and are usually shorter than the correct limits, which have not been developed for interval data.

Here, INTERVAL = LOWER UPPER specifies the input data set variables Lower and Upper as the age interval endpoints. The variable Recurrences identifies the number of recurrences (defrost control replacements) in each time interval, and Censored identifies the number of units censored in each interval (number in an age interval or removed from the sample in an age interval).

Figure 16.42: MCF Plot for the Defrost Controls

Figure 16.43: Listing of the Output for the Defrost Controls Data

Recurrence Data Summary
Input Data Set	WORK.DEFROST
Observations Used	29
Number of Units	22914
Number of Events	404

Recurrence Data Analysis
	Endpoints		Sample MCF	Standard Error	Naive 95% Confidence Limits
	Lower	Upper	Sample MCF	Standard Error	Lower	Upper
	0.00	1.00	0.004	0.000	0.003	0.004
	1.00	2.00	0.005	0.000	0.004	0.006
	2.00	3.00	0.006	0.001	0.005	0.007
	3.00	4.00	0.007	0.001	0.006	0.008
	4.00	5.00	0.008	0.001	0.007	0.009
	5.00	6.00	0.008	0.001	0.007	0.010
	6.00	7.00	0.009	0.001	0.008	0.010
	7.00	8.00	0.010	0.001	0.008	0.011
	8.00	9.00	0.010	0.001	0.009	0.012
	9.00	10.00	0.011	0.001	0.010	0.012
	10.00	11.00	0.012	0.001	0.011	0.013
	11.00	12.00	0.013	0.001	0.011	0.014
	12.00	13.00	0.015	0.001	0.013	0.018
	13.00	14.00	0.020	0.002	0.016	0.023
	14.00	15.00	0.025	0.002	0.021	0.030
	15.00	16.00	0.027	0.002	0.023	0.032
	16.00	17.00	0.031	0.003	0.025	0.036
	17.00	18.00	0.034	0.003	0.028	0.040
	18.00	19.00	0.038	0.003	0.031	0.044
	19.00	20.00	0.040	0.003	0.033	0.046
	20.00	21.00	0.042	0.003	0.035	0.049
	21.00	22.00	0.045	0.004	0.038	0.052
	22.00	23.00	0.048	0.004	0.040	0.055
	23.00	24.00	0.051	0.004	0.043	0.059
	24.00	25.00	0.059	0.005	0.049	0.069
	25.00	26.00	0.065	0.006	0.054	0.077
	26.00	27.00	0.072	0.006	0.059	0.084
	27.00	28.00	0.081	0.007	0.066	0.096
*	28.00	29.00	0.091	0.010	0.072	0.110
* The estimate and limits for this interval may not be appropriate.

The last interval is always marked with a footnote indicating that estimates for the last interval may be biased since censoring ages often are not uniformly spread over that interval.