The MVPDIAGNOSE Procedure

Getting Started: MVPDIAGNOSE Procedure

This example illustrates the basic features of the MVPDIAGNOSE procedure by using airline flight delay data available from the U.S. Bureau of Transportation Statistics at http://www.transtats.bts.gov. Suppose you want to compare process variable contributions for an out-of-control $T^2$ statistic with contributions for adjacent observations. This kind of comparison can help you understand the underlying causes of unusual variation in the process.

The following statements create a SAS data set named MWflightDelays that provides the delays for flights that originated in the midwestern United States. The data set contains variables for nine airlines: AA (American Airlines), CO (Continental Airlines), DL (Delta Airlines), F9 (Frontier Airlines), FL (AirTran Airways), NW (Northwest Airlines), UA (United Airlines), US (US Airways), and WN (Southwest Airlines).

data MWflightDelays;
   format flightDate MMDDYY8.;
   label flightDate='Date';
   input flightDate :MMDDYY8. AA CO DL F9 FL NW UA US WN; 
   datalines; 
02/01/07 14.9  7.1  7.9  8.5 14.8  4.5  5.1 13.4  5.1
02/02/07 14.3  9.6 14.1  6.2 12.8  6.0  3.9 15.3 11.4
02/03/07 23.0  6.1  1.7  0.9 11.9 15.2  9.5 18.4  7.6
02/04/07  6.5  6.3  3.9 -0.2  8.4 18.8  6.2  8.8  8.0
02/05/07 12.0 14.1  3.3 -1.3 10.0 13.1 22.8 16.5 11.5
02/06/07 31.9  8.6  4.9  2.0 11.9 21.9 29.0 15.5 15.2
02/07/07 14.2  3.0  2.1 -0.9 -0.6  7.8 19.9  8.6  6.4
02/08/07  6.5  6.8  1.8  7.7  1.3  6.9  6.1  9.2  5.4 
02/09/07 12.8  9.4  5.5  9.3 -0.2  4.6  7.6  7.8  7.5
02/10/07  9.4  3.5  1.5 -0.2  2.2  9.9  3.1 12.5  3.0 
02/11/07 12.9  5.4  0.9  6.8  2.1  7.9  3.7 10.7  5.6
02/12/07 34.6 15.9  1.8  1.0  4.5 10.2 14.0 19.1  4.9
02/13/07 34.0 16.0  4.4  6.1 18.3  9.1 30.2 46.3 50.6
02/14/07 21.2 45.9 16.6 12.5 35.1 23.8 40.4 43.6 35.2
02/15/07 46.6 36.3 23.9 20.8 30.4 24.3 30.3 59.9 25.6
02/16/07 31.2 20.8 15.2 20.1  9.1 12.9 22.9 36.4 16.4
;

The observations for a given date are the average delays in minutes for flights that depart from the Midwest. For example, on February 2, 2007, F9 (Frontier Airlines) flights departed an average of 6.2 minutes late.

The first step in multivariate process monitoring of the data is to build a principal component model of the process variation. The following statements use PROC MVPMODEL to create a model with three principal components. (See Chapter 12: The MVPMODEL Procedure, for details.)

proc mvpmodel data=MWflightDelays ncomp=3 noprint
              out=mvpair outloadings=mvpairloadings;
   var AA CO DL F9 FL NW UA US WN;
run;

The mvpair data set contains the process data and associated principal component scores. The mvpairloadings data set contains the principal component loadings for the process variables and other data that describe the model.

The following statements create a $T^2$ control chart by using the principal components. (See Chapter 13: The MVPMONITOR Procedure, for details.)

ods graphics on;
proc mvpmonitor history=mvpair loadings=mvpairloadings;
   time flightDate;
   tsquarechart / contributions;
run;

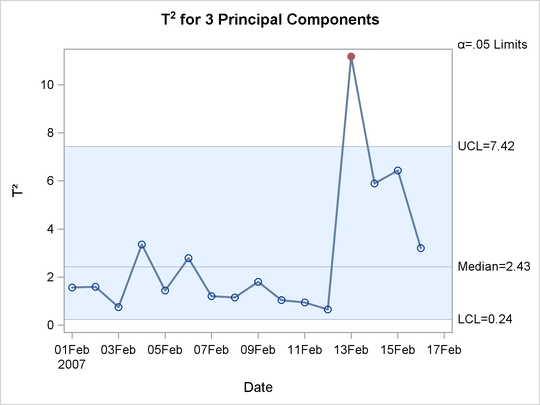
The CONTRIBUTIONS option produces contribution plots for any out-of-control points in the $T^2$ chart. Figure 11.1 shows the $T^2$ chart.

Figure 11.1: Multivariate Control Chart for $T^2$ Statistics

The $T^2$ chart shows an out-of-control point on February 13, 2007. Figure 11.2 shows the contribution plot for this date that was produced by the CONTRIBUTIONS option.

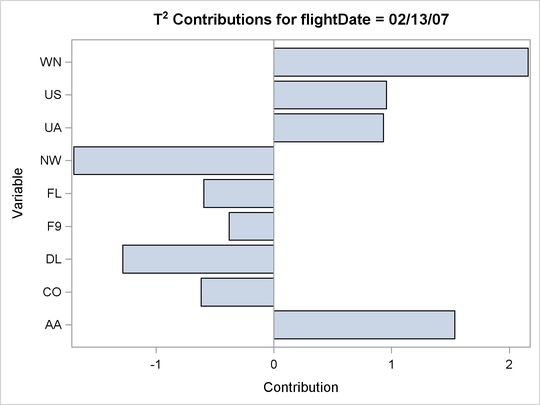
Figure 11.2: Contribution Plot for Out-of-Control Point

The contribution plot shows that the delays for airlines AA, DL, NW, and WN are the major contributors to the out-of-control point. You can use PROC MVPDIAGNOSE to compare the contributions for this point to those for adjacent points. The following statements produce paneled contribution plots of all the observations in mvpair:

proc mvpdiagnose history=mvpair loadings=mvpairloadings;
   time flightDate;
   contributionpanel / type=tsquare;
run;

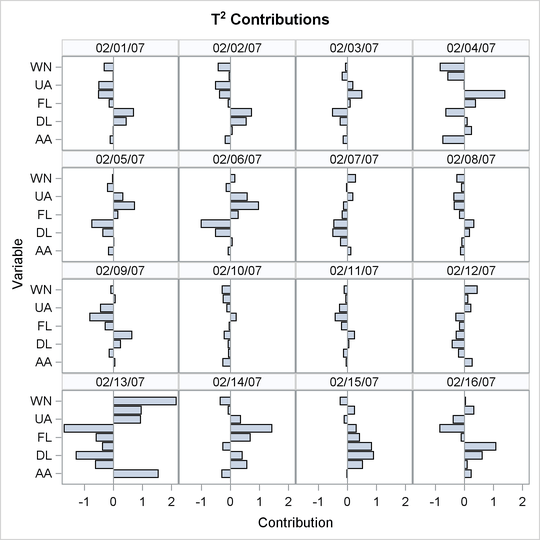
Figure 11.3 shows the paneled contribution plots.

Figure 11.3: $T^2$ Contributions for Flight Delays

The contribution plot for February 13 is in the lower-left corner of the plot. Notice that the magnitudes of all the process variable contributions are quite large for this date compared to those for the other dates. All the process variables contributed strongly to the out-of-control $T^2$ statistic. This implies that something unusual occurred on February 13 that affected the flight delays for all the airlines.

In fact, on this day a strong winter storm battered the Midwest. This is an example of variation due to a special cause. Special causes, also referred to as assignable causes, are local, sporadic, or transient problems in a process. They are distinguished from common causes of variation, which are inherent in a system. Control charts are used to monitor the process for the occurrence of special causes and to measure and potentially to reduce the effects of common causes.