The GENMOD Procedure

Bayesian Analysis

ARMS Algorithm for Gibbs Sampling
Gamerman Algorithm
Independence Metropolis Algorithm
Posterior Samples Output Data Set
Priors for Model Parameters
Deviance Information Criterion
Posterior Distribution
Starting Values of the Markov Chains
OUTPOST= Output Data Set

In generalized linear models, the response has a probability distribution from a family of distributions of the exponential form. That is, the probability density of the response Y for continuous response variables, or the probability function for discrete responses, can be expressed as

$f(y) = \exp \left\{ \frac{y\theta - b(\theta )}{a(\phi )} + c(y,\phi ) \right\}$

for some functions a, b, and c that determine the specific distribution. The canonical parameters $\theta$ depend only on the means of the response $\mu _ i$ , which are related to the regression parameters $\beta$ through the link function $g(\mu _ i)=x^\prime \beta$ . The additional parameter $\phi$ is the dispersion parameter. The GENMOD procedure estimates the regression parameters and the scale parameter $\sigma = \phi ^\frac {1}{2}$ by maximum likelihood. However, the GENMOD procedure can also provide Bayesian estimates of the regression parameters and either the scale $\sigma$ , the dispersion $\phi$ , or the precision $\tau = \phi ^{-1}$ by sampling from the posterior distribution. Except where noted, the following discussion applies to either $\sigma$ , $\phi$ , or $\tau$ , although $\phi$ is used to illustrate the formulas. Note that the Poisson and binomial distributions do not have a dispersion parameter, and the dispersion is considered to be fixed at $\phi = 1$ . The ASSESS, CONTRAST, ESTIMATE, OUTPUT, and REPEATED statements, if specified, are ignored. Also ignored are the PLOTS= option in the PROC GENMOD statement and the following options in the MODEL statement: ALPHA=, CORRB, COVB, TYPE1, TYPE3, SCALE=DEVIANCE (DSCALE), SCALE=PEARSON (PSCALE), OBSTATS, RESIDUALS, XVARS, PREDICTED, DIAGNOSTICS, and SCALE= for Poisson and binomial distributions. The multinomial and zero-inflated Poisson distributions are not available for Bayesian analysis.

See the section Assessing Markov Chain Convergence for information about assessing the convergence of the chain of posterior samples.

Several algorithms, specified with the SAMPLING= option in the BAYES statement, are available in GENMOD for drawing samples from the posterior distribution.

ARMS Algorithm for Gibbs Sampling

This section provides details for Bayesian analysis by Gibbs sampling in generalized linear models. See the section Gibbs Sampler for a general discussion of Gibbs sampling. See Gilks, Richardson, and Spiegelhalter (1996) for a discussion of applications of Gibbs sampling to a number of different models, including generalized linear models.

Let $\btheta = (\theta _1, \ldots , \theta _ k)’$ be the parameter vector. For generalized linear models, the $\theta _ i$ s are the regression coefficients $\beta _ i$ s and the dispersion parameter $\phi$ . Let $L(D|\btheta )$ be the likelihood function, where D is the observed data. Let $\pi (\btheta )$ be the prior distribution. The full conditional distribution of $[\theta _ i | \theta _ j, i\neq j]$ is proportional to the joint distribution; that is,

$\pi (\theta _ i | \theta _ j, i \neq j, D) \propto L(D|\btheta ) p(\btheta )$

For instance, the one-dimensional conditional distribution of $\theta _1$ given $\theta _ j=\theta _ j^*, 2\leq j \leq k$ , is computed as

$\pi (\theta _1 | \theta _ j=\theta _ j^*, 2\leq j \leq k, D) = L(D|(\btheta =(\theta _1, \theta ^*_2,\ldots ,\theta ^*_ k)’) p(\btheta =(\theta _1, \theta ^*_2,\ldots ,\theta ^*_ k)’)$

Suppose you have a set of arbitrary starting values $\{ \theta _1^{(0)}, \ldots , \theta _ k^{(0)}\}$ . Using the ARMS (adaptive rejection Metropolis sampling) algorithm (Gilks and Wild, 1992; Gilks, Best, and Tan, 1995), you can do the following:

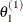draw $\theta _1^{(1)}$ from $[\theta _1|\theta _2^{(0)},\ldots ,\theta _ k^{(0)}]$
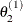draw $\theta _2^{(1)}$ from $[\theta _2|\theta _1^{(1)}, \theta _3^{(0)},\ldots ,\theta _ k^{(0)}]$
$\ldots$
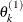draw $\theta _ k^{(1)}$ from $[\theta _ k|\theta _1^{(1)},\ldots ,\theta _{k-1}^{(1)}]$

This completes one iteration of the Gibbs sampler. After one iteration, you have $\{ \theta _1^{(1)}, \ldots , \theta _ k^{(1)}\}$ . After n iterations, you have $\{ \theta _1^{(n)}, \ldots , \theta _ k^{(n)}\}$ . PROC GENMOD implements the ARMS algorithm provided by Gilks (2003) to draw a sample from a full conditional distribution. See the section Adaptive Rejection Sampling Algorithm for more information about the ARMS algorithm. The ARMS algorithm is the default method used to sample from the posterior distribution, except in the case of a normal distribution with a conjugate prior, in which case a closed form is available for the posterior distribution. See any of the introductory references in Chapter 7: Introduction to Bayesian Analysis Procedures, for a discussion of conjugate prior distributions for a linear model with the normal distribution.

Gamerman Algorithm

The Gamerman algorithm, unlike a Gibbs sampling algorithm, samples parameters from their multivariate posterior conditional distribution. The algorithm uses the structure of generalized linear models to efficiently sample from the posterior distribution of the model parameters. For a detailed description and explanation of the algorithm, see Gamerman (1997) and the section Gamerman Algorithm.

Independence Metropolis Algorithm

The independence Metropolis algorithm is another sampling algorithm that draws multivariate samples from the posterior distribution. See the section Independence Sampler for more details.

Posterior Samples Output Data Set

You can output posterior samples into a SAS data set through ODS. The following SAS statement outputs the posterior samples into the SAS data set Post:

ODS OUTPUT POSTERIORSAMPLE=Post

You can alternatively create the SAS data set Post with the OUTPOST=Post option in the BAYES statement.

The data set also includes the variables LogPost and LogLike, which represent the log of the posterior likelihood and the log of the likelihood, respectively.

Priors for Model Parameters

The model parameters are the regression coefficients and the dispersion parameter (or the precision or scale), if the model has one. The priors for the dispersion parameter and the priors for the regression coefficients are assumed to be independent, while you can have a joint multivariate normal prior for the regression coefficients.

Dispersion, Precision, or Scale Parameter

Gamma Prior

The gamma distribution has a probability density function

$f(u) = \frac{b (b u)^{a-1}\mr {e}^{-b u}}{\Gamma (a)}, \hspace{1cm} u>0$

where a is the shape parameter and b is the inverse-scale parameter. The mean is $\frac{a}{b}$ and the variance is $\frac{a}{b^2}$ .

Improper Prior

The joint prior density is given by

$p(u) \propto u^{-1}, \hspace{1cm} u>0$

Inverse Gamma Prior

The inverse gamma distribution $\mr {IG}(a,b)$ has a probability density function

$f(u)=\frac{b^ a}{\Gamma (a)} u^{-(a+1)}\mr {e}^{-b/u}, \hspace{1cm} u>0$

where a is the shape parameter and b is the scale parameter. The mean is $\frac{b}{a-1}$ if , and the variance is $\frac{b^2}{(a-1)^2(a-2)}$ if .

Regression Coefficients

Let $\bbeta$ be the regression coefficients.

Jeffreys’ Prior

The joint prior density is given by

$p(\bbeta ) \propto \left|\mb {I}(\bbeta )\right|^\frac {1}{2}$

where $\mb {I}(\bbeta )$ is the Fisher information matrix for the model. If the underlying model has a scale parameter (for example, a normal linear regression model), then the Fisher information matrix is computed with the scale parameter set to a fixed value of one.

If you specify the CONDITIONAL option, then Jeffreys’ prior, conditional on the current Markov chain value of the generalized linear model precision parameter $\tau$ , is given by

$\left|\tau \mb {I}(\bbeta )\right|^\frac {1}{2}$

where $\tau$ is the model precision parameter.

See Ibrahim and Laud (1991) for a full discussion, with examples, of Jeffreys’ prior for generalized linear models.

Normal Prior

Assume $\bbeta$ has a multivariate normal prior with mean vector $\bbeta _0$ and covariance matrix $\bSigma _0$ . The joint prior density is given by

$p(\bbeta ) \propto \mr {e}^{-\frac{1}{2} (\bbeta -\bbeta _0)^\prime \bSigma _0^{-1}(\bbeta -\bbeta _0)}$

If you specify the CONDITIONAL option, then, conditional on the current Markov chain value of the generalized linear model precision parameter $\tau$ , the joint prior density is given by

$p(\bbeta ) \propto \mr {e}^{-\frac{1}{2} (\bbeta -\bbeta _0)^\prime \tau \bSigma _0^{-1}(\bbeta -\bbeta _0)}$

Uniform Prior

The joint prior density is given by

$p(\bbeta ) \propto 1$

Deviance Information Criterion

Let $\theta _ i$ be the model parameters at iteration i of the Gibbs sampler and let LL( $\theta _ i$ ) be the corresponding model log likelihood. PROC GENMOD computes the following fit statistics defined by Spiegelhalter et al. (2002):

Effective number of parameters:

$p_ D=\overline{\mr {LL}(\theta )} - \mr {LL}(\bar{\theta })$

Deviance information criterion (DIC):

$\mr {DIC}= \overline{\mr {LL}(\theta )} + p_ D$

where

$\begin{array}{lll} \overline{\mr {LL}(\theta )}& = & \frac{1}{n}\sum _{i=1}^ n\mr {LL}(\theta _ i) \\ \bar{\theta } & = & \frac{1}{n}\sum _{i=1}^ n\theta _ i \\ \end{array}$

PROC GENMOD uses the full log likelihoods defined in the section Log-Likelihood Functions, with all terms included, for computing the DIC.

Posterior Distribution

Denote the observed data by D.

The posterior distribution is

$\pi (\bbeta |D) \propto L_ P(D|\bbeta ) p(\bbeta )$

where $L_ P(D|\bbeta )$ is the likelihood function with regression coefficients $\bbeta$ as parameters.

Starting Values of the Markov Chains

When the BAYES statement is specified, PROC GENMOD generates one Markov chain containing the approximate posterior samples of the model parameters. Additional chains are produced when the Gelman-Rubin diagnostics are requested. Starting values (or initial values) can be specified in the INITIAL= data set in the BAYES statement. If INITIAL= option is not specified, PROC GENMOD picks its own initial values for the chains.

Denote as the integral value of x. Denote $\hat{s}(X)$ as the estimated standard error of the estimator X.

Regression Coefficients

For the first chain that the summary statistics and regression diagnostics are based on, the default initial values are estimates of the mode of the posterior distribution. If the INITIALMLE option is specified, the initial values are the maximum likelihood estimates; that is,

$\beta _ i^{(0)} = \hat{\beta }_ i$

Initial values for the rth chain ( $r \geq 2$ ) are given by

$\beta _ i^{(0)} = \hat{\beta }_ i \pm \biggl (2+ \biggl [\frac{r}{2} \biggr ] \biggr ) \hat{s}(\hat{\beta }_ i)$

with the plus sign for odd r and minus sign for even r.

Dispersion, Scale, or Precision Parameter 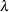$\lambda$

Let $\lambda$ be the generalized linear model parameter you choose to sample, either the dispersion, scale, or precision parameter. Note that the Poisson and binomial distributions do not have this additional parameter.

$\lambda ^{(0)} = \hat{\lambda }$

The initial values of the rth chain ( $r \geq 2$ ) are given by

$\lambda ^{(0)} = \hat{\lambda } \mr {e}^{\pm \biggl ([\frac{r}{2}]+2 \biggl ) \hat{s}(\hat{\lambda })}$

with the plus sign for odd r and minus sign for even r.

OUTPOST= Output Data Set

The OUTPOST= data set contains the generated posterior samples. There are 3+n variables, where n is the number of model parameters. The variable Iteration represents the iteration number, the variable LogLike contains the log of the likelihood, and the variable LogPost contains the log of the posterior. The other n variables represent the draws of the Markov chain for the model parameters.