The KDE Procedure
Getting Started: KDE Procedure
The following example illustrates the basic features of PROC KDE. Assume that 1000 observations are simulated from a bivariate
normal density with means ![]() , variances
, variances ![]() , and covariance 9. The SAS DATA step to accomplish this is as follows:
, and covariance 9. The SAS DATA step to accomplish this is as follows:
data bivnormal;
seed = 1283470;
do i = 1 to 1000;
z1 = rannor(seed);
z2 = rannor(seed);
z3 = rannor(seed);
x = 3*z1+z2;
y = 3*z1+z3;
output;
end;
drop seed;
run;
The following statements request a bivariate kernel density estimate for the variables x and y, with contour and surface plots:
ods graphics on; proc kde data=bivnormal; bivar x y / plots=(contour surface); run; ods graphics off;
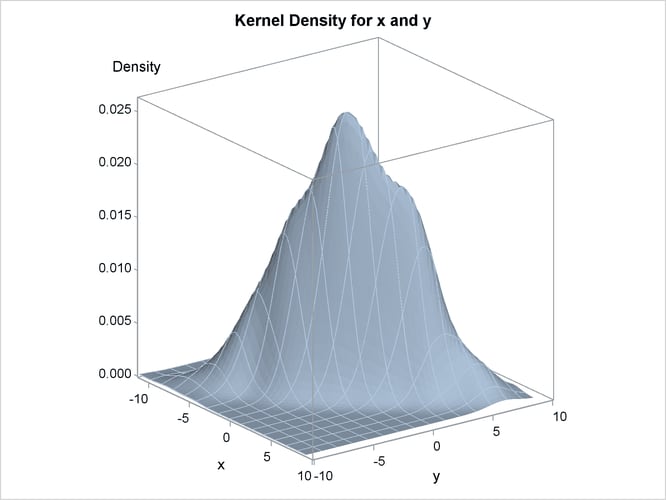
The contour plot and the surface plot of the estimate are displayed in Figure 48.1 and Figure 48.2, respectively. Note that the correlation of 0.9 in the original data results in oval-shaped contours. These graphs are produced by specifying the PLOTS= option in the BIVAR statement with ODS Graphics enabled. For general information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS. For specific information about the graphics available in the KDE procedure, see the section ODS Graphics.
Figure 48.1: Contour Plot of Estimated Density
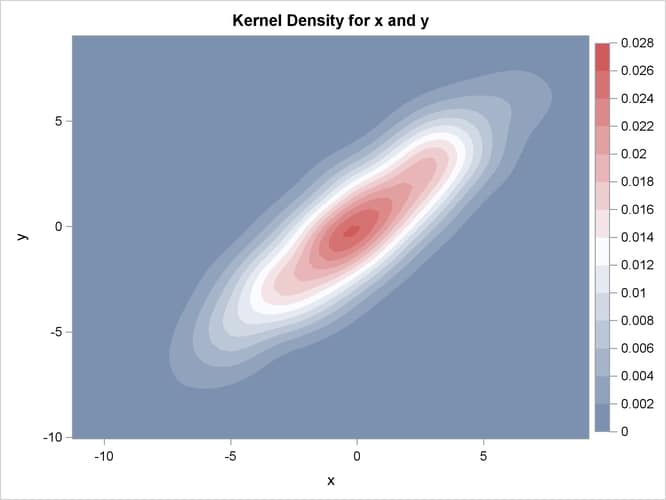
Figure 48.2: Surface Plot of Estimated Density
The default output tables for this analysis are shown in Figure 48.3.
Figure 48.3: Default Bivariate Tables
| Inputs | |
|---|---|
| Data Set | WORK.BIVNORMAL |
| Number of Observations Used | 1000 |
| Variable 1 | x |
| Variable 2 | y |
| Bandwidth Method | Simple Normal Reference |
| Controls | ||
|---|---|---|
| x | y | |
| Grid Points | 60 | 60 |
| Lower Grid Limit | -11.25 | -10.05 |
| Upper Grid Limit | 9.1436 | 9.0341 |
| Bandwidth Multiplier | 1 | 1 |
The “Inputs” table lists basic information about the density fit, including the input data set, the number of observations, and the variables. The bandwidth method is the technique used to select the amount of smoothing in the estimate. A simple normal reference rule is used for bivariate smoothing.
The “Controls” table lists the primary numbers controlling the kernel density fit. Here a ![]() grid is fit to the entire range of the data, and no adjustment is made to the default bandwidth.
grid is fit to the entire range of the data, and no adjustment is made to the default bandwidth.
