The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics - References
Random-Effects Model
This example illustrates how you can fit a normal likelihood random-effects model in PROC MCMC. PROC MCMC offers you the ability to model beyond the normal likelihood (see Logistic Regression Random-Effects Model, Nonlinear Poisson Regression Multilevel Random-Effects Model, and Piecewise Exponential Frailty Model).
Consider a scenario in which data are collected in groups and you want to model group-specific effects. You can use a random-effects model (sometimes also known as a variance-components model):
|
|
where ![]() is the group index and
is the group index and ![]() indexes the observations in the ith group. In the regression model, the fixed effects
indexes the observations in the ith group. In the regression model, the fixed effects ![]() and
and ![]() are the intercept and the coefficient for variable
are the intercept and the coefficient for variable ![]() , respectively. The random effect
, respectively. The random effect ![]() is the mean for the ith group, and
is the mean for the ith group, and ![]() are the error term.
are the error term.
Consider the following SAS data set:
title 'Random-Effects Model'; data heights; input Family G$ Height @@; datalines; 1 F 67 1 F 66 1 F 64 1 M 71 1 M 72 2 F 63 2 F 63 2 F 67 2 M 69 2 M 68 2 M 70 3 F 63 3 M 64 4 F 67 4 F 66 4 M 67 4 M 67 4 M 69 ;
The response variable Height measures the heights (in inches) of 18 individuals. The covariate x is the gender (variable G), and the individuals are grouped according to Family (group index). Since the variable G is a character variable and PROC MCMC does not support a CLASS statement, you need to create the corresponding design matrix.
In this example, the design matrix for a factor variable of level 2 (M and F) can be constructed using the following statement:
data input; set heights; if g eq 'F' then gf = 1; else gf = 0; drop g; run;
The data set variable gf is a numeric variable and can be used in the regression model in PROC MCMC.
In data sets with factor variables that have more levels, you can consider using PROC TRANSREG to construct the design matrix. See the section Create Design Matrix for more information.
To model the data, you can assume that Height is normally distributed:
|
|
The priors on the parameters ![]() ,
, ![]() ,
, ![]() are also assumed to be normal:
are also assumed to be normal:
|
|
|
|
|
|
|
|
|
|
|
|
Priors on the variance terms, ![]() and
and ![]() , are inverse-gamma:
, are inverse-gamma:
|
|
|
|
|
|
|
|
The inverse-gamma distribution is a conjugate prior for the variance in the normal likelihood and the variance in the prior distribution of the random effect.
The following statements fit a linear random-effects model to the data and produce the output shown in Figure 55.9 and Figure 55.10:
ods graphics on;
proc mcmc data=input outpost=postout nmc=50000 thin=5 seed=7893 plots=trace;
ods select Parameters REparameters PostSummaries PostIntervals
tracepanel;
parms b0 0 b1 0 s2 1 s2g 1;
prior b: ~ normal(0, var = 10000);
prior s: ~ igamma(0.01, scale = 0.01);
random gamma ~ normal(0, var = s2g) subject=family monitor=(gamma);
mu = b0 + b1 * gf + gamma;
model height ~ normal(mu, var = s2);
run;
ods graphics off;
Some of the statements are very similar to those shown in the previous two examples. The ODS GRAPHICS ON statement enables ODS Graphics. The PROC MCMC statement specifies the input and output data sets, the simulation size, the thinning rate, and a random number seed. The ODS SELECT statement displays the model parameter and random-effects parameter information tables, summary statistics table, the interval statistics table, and the trace plots.
The PARMS statement lumps all four model parameters in a single block. They are b0 (overall intercept), b1 (main effect for gf), s2 (variance of the likelihood function), and s2g (variance of the random effect). If a random walk Metropolis sampler is the only applicable sampler for all parameters, then
these four parameters are updated in a single block. However, because PROC MCMC updates the parameters s2 and s2g via conjugacy, these parameters are separated into individual blocks. (See the Block column in “Parameters” table in Figure 55.8.)
The PRIOR statements specify priors for all the parameters. The notation b: is a shorthand for all symbols that start with the letter ‘b’. In this example, b: includes b0 and b1. Similarly, s: stands for both s2 and s2g. This shorthand notation can save you some typing, and it keeps your statements tidy.
The RANDOM statement specifies a single random effect to be gamma, and specifies that it has a normal prior centered at 0 with variance s2g. The SUBJECT= argument in the RANDOM statement defines a group index (family) in the model, where all observations from the same family should have the same group indicator value. The MONITOR= option outputs analysis for all the random-effects parameters.
Finally, the MU assignment statement calculates the expected value of the height of the model. The calculation includes the random-effects term gamma. The MODEL statement specifies the likelihood function for height.
The “Parameters” and “Random-Effects Parameters” tables, shown in Figure 55.8, contain information about the model parameters and the four random-effects parameters.
Figure 55.8: Model and Random-Effects Parameter Information
| Random-Effects Model |
| Parameters | ||||
|---|---|---|---|---|
| Block | Parameter | Sampling Method |
Initial Value |
Prior Distribution |
| 1 | s2 | Conjugate | 1.0000 | igamma(0.01, scale = 0.01) |
| 2 | s2g | Conjugate | 1.0000 | igamma(0.01, scale = 0.01) |
| 3 | b0 | N-Metropolis | 0 | normal(0, var = 10000) |
| b1 | 0 | normal(0, var = 10000) | ||
| Random Effect Parameters | |||||
|---|---|---|---|---|---|
| Parameter | Sampling Method |
Subject | Number of Subjects |
Subject Values |
Prior Distribution |
| gamma | N-Metropolis | Family | 4 | 1 2 3 4 | normal(0, var = s2g) |
The posterior summary and interval statistics for the model parameters and the random-effects parameters are shown in Figure 55.9.
Figure 55.9: Posterior Summary and Interval Statistics
| Random-Effects Model |
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| b0 | 10000 | 68.4717 | 1.2735 | 67.7757 | 68.4495 | 69.1213 |
| b1 | 10000 | -3.5533 | 0.9740 | -4.1829 | -3.5381 | -2.9375 |
| s2 | 10000 | 4.1334 | 1.9372 | 2.8024 | 3.7093 | 4.9790 |
| s2g | 10000 | 5.1508 | 23.4698 | 0.2312 | 1.3104 | 4.2433 |
| gamma_1 | 10000 | 0.9404 | 1.3219 | 0.0860 | 0.6963 | 1.6322 |
| gamma_2 | 10000 | 0.0131 | 1.1935 | -0.4020 | 0.0214 | 0.4878 |
| gamma_3 | 10000 | -1.3481 | 1.6535 | -2.1852 | -0.9346 | -0.1252 |
| gamma_4 | 10000 | 0.0945 | 1.1931 | -0.3323 | 0.0528 | 0.5643 |
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| b0 | 0.050 | 65.8646 | 71.1331 | 65.9097 | 71.1712 |
| b1 | 0.050 | -5.5058 | -1.6127 | -5.4201 | -1.5651 |
| s2 | 0.050 | 1.7166 | 9.0766 | 1.3678 | 7.8796 |
| s2g | 0.050 | 0.00983 | 32.7002 | 0.00105 | 19.0298 |
| gamma_1 | 0.050 | -1.0884 | 4.0560 | -1.0160 | 4.0923 |
| gamma_2 | 0.050 | -2.5942 | 2.5279 | -2.5357 | 2.5636 |
| gamma_3 | 0.050 | -5.4957 | 0.6638 | -4.7168 | 1.0677 |
| gamma_4 | 0.050 | -2.4901 | 2.7349 | -2.5895 | 2.5888 |
Trace plots for all the parameters are shown in Figure 55.10. The mixing looks very reasonable, suggesting convergence.
Figure 55.10: Plots for ![]() and Log of the Posterior Density
and Log of the Posterior Density
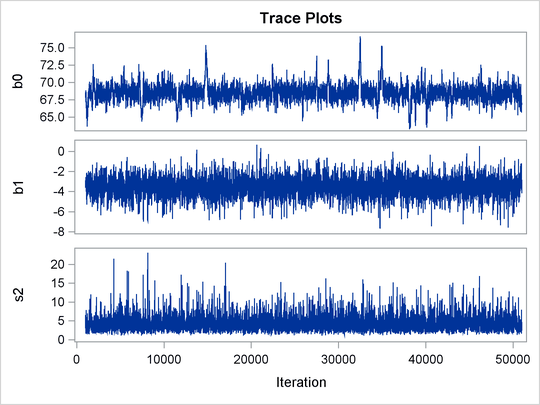
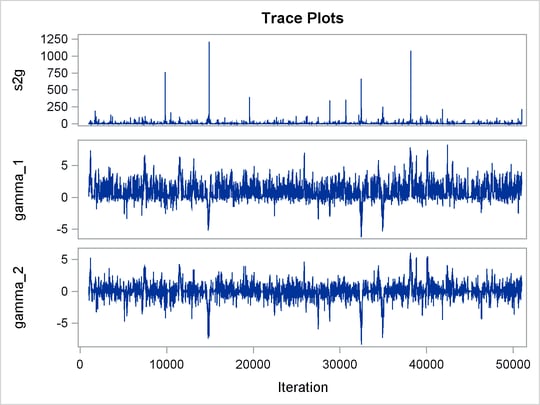
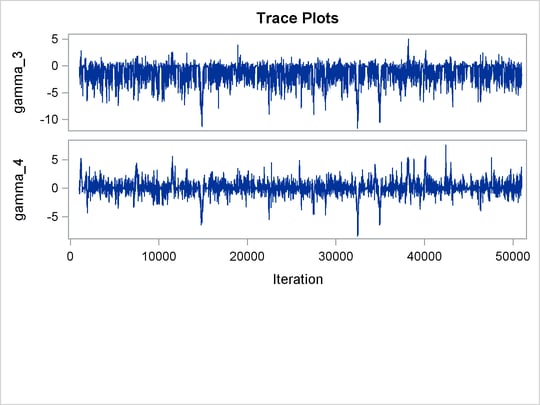
From the interval statistics table, you see that both the equal-tail and HPD intervals for ![]() are positive, strongly indicating the positive effect of the parameter. On the other hand, both intervals for
are positive, strongly indicating the positive effect of the parameter. On the other hand, both intervals for ![]() cover the value zero, indicating that
cover the value zero, indicating that gf does not have a strong impact on predicting height in this model.