The NLIN Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Automatic DerivativesMeasures of Nonlinearity and DiagnosticsMissing ValuesSpecial VariablesTroubleshootingComputational MethodsOutput Data SetsConfidence IntervalsCovariance Matrix of Parameter EstimatesConvergence MeasuresDisplayed OutputIncompatibilities with SAS 6.11 and Earlier Versions of PROC NLINODS Table NamesODS Graphics
Automatic DerivativesMeasures of Nonlinearity and DiagnosticsMissing ValuesSpecial VariablesTroubleshootingComputational MethodsOutput Data SetsConfidence IntervalsCovariance Matrix of Parameter EstimatesConvergence MeasuresDisplayed OutputIncompatibilities with SAS 6.11 and Earlier Versions of PROC NLINODS Table NamesODS Graphics -
Examples

- References
Estimating the Parameters in the Nonlinear Model
As an example of a nonlinear regression analysis, consider the following theoretical model of enzyme kinetics. The model relates the initial velocity of an enzymatic reaction to the substrate concentration.
|
|
where ![]() represents the amount of substrate for n trials and
represents the amount of substrate for n trials and ![]() is the velocity of the reaction. The vector
is the velocity of the reaction. The vector ![]() contains the rate parameters. This model is known as the Michaelis-Menten model in biochemistry (Ratkowsky, 1990, p. 59). The model exists in many parameterizations. In the form shown here,
contains the rate parameters. This model is known as the Michaelis-Menten model in biochemistry (Ratkowsky, 1990, p. 59). The model exists in many parameterizations. In the form shown here, ![]() is the maximum velocity of the reaction that is theoretically attainable. The parameter
is the maximum velocity of the reaction that is theoretically attainable. The parameter ![]() is the substrate concentration at which the velocity is 50% of the maximum.
is the substrate concentration at which the velocity is 50% of the maximum.
Suppose that you want to study the relationship between concentration and velocity for a particular enzyme/substrate pair. You record the reaction rate (velocity) observed at different substrate concentrations.
A SAS data set is created for this experiment in the following DATA step:
data Enzyme; input Concentration Velocity @@; datalines; 0.26 124.7 0.30 126.9 0.48 135.9 0.50 137.6 0.54 139.6 0.68 141.1 0.82 142.8 1.14 147.6 1.28 149.8 1.38 149.4 1.80 153.9 2.30 152.5 2.44 154.5 2.48 154.7 ;
The SAS data set Enzyme contains the two variables Concentration (substrate concentration) and Velocity (reaction rate). The following statements fit the Michaelis-Menten model by nonlinear least squares:
proc nlin data=Enzyme method=marquardt hougaard;
parms theta1=155
theta2=0 to 0.07 by 0.01;
model Velocity = theta1*Concentration / (theta2 + Concentration);
run;
The DATA= option specifies that the SAS data set Enzyme be used in the analysis. The METHOD= option directs PROC NLIN to use the MARQUARDT iterative method. The HOUGAARD option requests that a skewness measure be calculated for the parameters.
The PARMS statement declares the parameters and specifies their initial values. Suppose that V represents the velocity and C represents the substrate concentration. In this example, the initial estimates listed in the PARMS statement for ![]() and
and ![]() are obtained as follows:
are obtained as follows:
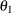 :
:-
Because the model is a monotonic increasing function in C, and because
![\[ \lim _{C \rightarrow \infty } \left( \frac{\theta _1 C}{\theta _2 + C} \right) = \theta _1 \]](images/statug_nlin0060.png)
you can take the largest observed value of the variable
Velocity(154.7) as the initial value for the parameterTheta1. Thus, the PARMS statement specifies 155 as the initial value forTheta1, which is approximately equal to the maximum observed velocity. 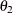 :
:-
To obtain an initial value for the parameter
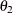 , first rearrange the model equation to solve for
, first rearrange the model equation to solve for 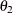 :
:
![\[ \theta _2 = \frac{\theta _1 C}{ V } - C \]](images/statug_nlin0061.png)
By substituting the initial value of
Theta1for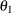 and taking each pair of observed values of
and taking each pair of observed values of ConcentrationandVelocityfor C and V, respectively, you obtain a set of possible starting values forTheta2ranging from about 0.01 to 0.07.
You can choose any value within this range as a starting value for Theta2, or you can direct PROC NLIN to perform a preliminary search for the best initial Theta2 value within that range of values. The PARMS statement specifies a range of values for Theta2, resulting in a search over the grid points from 0 to 0.07 in increments of 0.01.
The MODEL statement specifies the enzymatic reaction model
|
|
in terms of the data set variables Velocity and Concentration and in terms of the parameters in the PARMS statement.
The results from this PROC NLIN invocation are displayed in the following figures.
PROC NLIN evaluates the model at each point on the specified grid for the Theta2 parameter. Figure 63.1 displays the calculations resulting from the grid search.
Figure 63.1: Nonlinear Least-Squares Grid Search
| Grid Search | ||
|---|---|---|
| theta1 | theta2 | Sum of Squares |
| 155.0 | 0 | 3075.4 |
| 155.0 | 0.0100 | 2074.1 |
| 155.0 | 0.0200 | 1310.3 |
| 155.0 | 0.0300 | 752.0 |
| 155.0 | 0.0400 | 371.9 |
| 155.0 | 0.0500 | 147.2 |
| 155.0 | 0.0600 | 58.1130 |
| 155.0 | 0.0700 | 87.9662 |
The parameter Theta1 is held constant at its specified initial value of 155, the grid is traversed, and the residual sum of squares is computed
at each point. The “best” starting value is the point that corresponds to the smallest value of the residual sum of squares. The best set of starting
values is obtained for ![]() (Figure 63.1). PROC NLIN uses this point from which to start the following, iterative phase of nonlinear least-squares estimation.
(Figure 63.1). PROC NLIN uses this point from which to start the following, iterative phase of nonlinear least-squares estimation.
Figure 63.2 displays the iteration history. Note that the first entry in the “Iterative Phase” table echoes the starting values and the residual sum of squares for the best value combination in Figure 63.1. The subsequent rows of the table show the updates of the parameter estimates and the improvement (decrease) in the residual
sum of squares. For this data-and-model combination, the first iteration yielded a large improvement in the sum of squares
(from 58.113 to 19.7017). Further steps were necessary to improve the estimates in order to achieve the convergence criterion.
The NLIN procedure by default determines convergence by using R, the relative offset measure of Bates and Watts (1981). Convergence is declared when this measure is less than ![]() —in this example, after three iterations.
—in this example, after three iterations.
Figure 63.2: Iteration History and Convergence Status
| Iterative Phase | |||
|---|---|---|---|
| Iter | theta1 | theta2 | Sum of Squares |
| 0 | 155.0 | 0.0600 | 58.1130 |
| 1 | 158.0 | 0.0736 | 19.7017 |
| 2 | 158.1 | 0.0741 | 19.6606 |
| 3 | 158.1 | 0.0741 | 19.6606 |
| NOTE: Convergence criterion met. |
Figure 63.3: Estimation Summary
| Estimation Summary | |
|---|---|
| Method | Marquardt |
| Iterations | 3 |
| R | 5.861E-6 |
| PPC(theta2) | 8.569E-7 |
| RPC(theta2) | 0.000078 |
| Object | 2.902E-7 |
| Objective | 19.66059 |
| Observations Read | 14 |
| Observations Used | 14 |
| Observations Missing | 0 |
A summary of the estimation including several convergence measures (R, PPC, RPC, and Object) is displayed in Figure 63.3.
The “R” measure in Figure 63.3 is the relative offset convergence measure of Bates and Watts. A “PPC” value of 8.569E–7 indicates that the parameter Theta2 (which has the largest PPC value of the parameters) would change by that relative amount, if PROC NLIN were to take an additional
iteration step. The “RPC” value indicates that Theta2 changed by 0.000078, relative to its value in the last iteration. These changes are measured before step length adjustments
are made. The “Object” measure indicates that the objective function changed by 2.902E–7 in relative value from the last iteration.
Figure 63.4 displays the analysis of variance table for the model. The table displays the degrees of freedom, sums of squares, and mean squares along with the model F test.
Figure 63.4: Nonlinear Least-Squares Analysis of Variance
| Note: | An intercept was not specified for this model. |
| Source | DF | Sum of Squares | Mean Square | F Value | Approx Pr > F |
|---|---|---|---|---|---|
| Model | 2 | 290116 | 145058 | 88537.2 | <.0001 |
| Error | 12 | 19.6606 | 1.6384 | ||
| Uncorrected Total | 14 | 290135 |
Figure 63.5: Parameter Estimates and Approximate 95% Confidence Intervals
| Parameter | Estimate | Approx Std Error |
Approximate 95% Confidence Limits |
Skewness | |
|---|---|---|---|---|---|
| theta1 | 158.1 | 0.6737 | 156.6 | 159.6 | 0.0152 |
| theta2 | 0.0741 | 0.00313 | 0.0673 | 0.0809 | 0.0362 |
Figure 63.5 displays the estimates for each parameter, the associated asymptotic standard error, and the upper and lower values for the asymptotic 95% confidence interval. PROC NLIN also displays the asymptotic correlations between the estimated parameters (not shown).
The skewness measures of 0.0152 and 0.0362 indicate that the parameter estimators exhibit close-to-linear behavior and that their standard errors and confidence intervals can be safely used for inferences.
Thus, the estimated nonlinear model relating reaction velocity and substrate concentration can be written as
|
|
where ![]() represents the predicted velocity or rate of the reaction, and C represents the substrate concentration.
represents the predicted velocity or rate of the reaction, and C represents the substrate concentration.