The PLM Procedure
Example 69.6 Comparing Multiple B-Splines
This example conducts an analysis similar to Example 15 in Examples: GLIMMIX Procedure: Examples: GLIMMIX Procedure. It uses simulated data to perform multiple comparisons among predicted values in a model with group-specific trends that
are modeled through regression splines. The estimable functions are formed using nonpositional syntax with constructed effects.
Consider the data in the following DATA step. Each of the 100 observations for the continuous response variable y is associated with one of two groups.
data spline; input group y @@; x = _n_; datalines; 1 -.020 1 0.199 2 -1.36 1 -.026 2 -.397 1 0.065 2 -.861 1 0.251 1 0.253 2 -.460 2 0.195 2 -.108 1 0.379 1 0.971 1 0.712 2 0.811 2 0.574 2 0.755 1 0.316 2 0.961 2 1.088 2 0.607 2 0.959 1 0.653 1 0.629 2 1.237 2 0.734 2 0.299 2 1.002 2 1.201 1 1.520 1 1.105 1 1.329 1 1.580 2 1.098 1 1.613 2 1.052 2 1.108 2 1.257 2 2.005 2 1.726 2 1.179 2 1.338 1 1.707 2 2.105 2 1.828 2 1.368 1 2.252 1 1.984 2 1.867 1 2.771 1 2.052 2 1.522 2 2.200 1 2.562 1 2.517 1 2.769 1 2.534 2 1.969 1 2.460 1 2.873 1 2.678 1 3.135 2 1.705 1 2.893 1 3.023 1 3.050 2 2.273 2 2.549 1 2.836 2 2.375 2 1.841 1 3.727 1 3.806 1 3.269 1 3.533 1 2.948 2 1.954 2 2.326 2 2.017 1 3.744 2 2.431 2 2.040 1 3.995 2 1.996 2 2.028 2 2.321 2 2.479 2 2.337 1 4.516 2 2.326 2 2.144 2 2.474 2 2.221 1 4.867 2 2.453 1 5.253 2 3.024 2 2.403 1 5.498 ;
The following statements fit a model with separate trends for the two groups; the trends are modeled as B-splines.
proc orthoreg data=spline; class group; effect spl = spline(x); model y = group spl*group / noint; store ortho_spline; title 'B-splines Comparisons'; run;
Results from this analysis are shown in Output 69.6.1. The “Parameter Estimates” table shows the estimates for the spline coefficients in the two groups.
Output 69.6.1: Results for Group-Specific Spline Model
| B-splines Comparisons |
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 13 | 153.0175561 | 11.770581238 | 160.11 | <.0001 |
| Error | 86 | 6.3223804119 | 0.0735160513 | ||
| Corrected Total | 99 | 159.33993651 |
| Root MSE | 0.2711384357 |
|---|---|
| R-Square | 0.9603214326 |
| Parameter | DF | Parameter Estimate | Standard Error | t Value | Pr > |t| |
|---|---|---|---|---|---|
| (group='1') | 1 | 9.70265463962039 | 3.1341899987 | 3.10 | 0.0026 |
| (group='2') | 1 | 6.30619220563569 | 2.6299147768 | 2.40 | 0.0187 |
| spl*group 1 1 | 1 | -11.1786451718041 | 3.7008097395 | -3.02 | 0.0033 |
| spl*group 1 2 | 1 | -20.1946092746139 | 3.9765046236 | -5.08 | <.0001 |
| spl*group 2 1 | 1 | -9.53273697995301 | 3.2575832048 | -2.93 | 0.0044 |
| spl*group 2 2 | 1 | -5.85652496534967 | 2.7906116773 | -2.10 | 0.0388 |
| spl*group 3 1 | 1 | -8.96118371893294 | 3.0717508806 | -2.92 | 0.0045 |
| spl*group 3 2 | 1 | -5.55671605245205 | 2.5716715573 | -2.16 | 0.0335 |
| spl*group 4 1 | 1 | -7.26153231478755 | 3.243690314 | -2.24 | 0.0278 |
| spl*group 4 2 | 1 | -4.36778889738236 | 2.7246809593 | -1.60 | 0.1126 |
| spl*group 5 1 | 1 | -6.44615256510896 | 2.9616955361 | -2.18 | 0.0323 |
| spl*group 5 2 | 1 | -4.03801618914902 | 2.4588839125 | -1.64 | 0.1042 |
| spl*group 6 1 | 1 | -4.63816959094139 | 3.7094636319 | -1.25 | 0.2146 |
| spl*group 6 2 | 1 | -4.30290104395061 | 3.0478540171 | -1.41 | 0.1616 |
| spl*group 7 1 | 0 | 0 | . | . | . |
| spl*group 7 2 | 0 | 0 | . | . | . |
By default, the ORTHOREG procedure constructs B-splines with seven knots. Since B-spline coefficients satisfy a sum-to-one constraint and since the model contains group-specific intercepts, the last spline coefficient for each group is redundant and is set to 0.
The following statements make a prediction for the input data set by using the SCORE statement with PROC PLM and graph the observed and predicted values in the two groups:
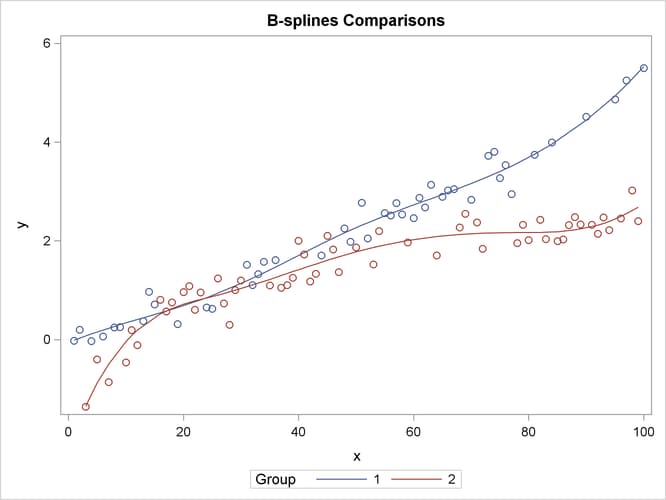
proc plm restore=ortho_spline; score data=spline out=ortho_pred predicted=p; run; proc sgplot data=ortho_pred; series y=p x=x / group=group name="fit"; scatter y=y x=x / group=group; keylegend "fit" / title="Group"; run;
The prediction plot in Output 69.6.2 suggests that there is some separation of the group trends for small values of x and for values that exceed about x = 40.
Output 69.6.2: Observed Data and Predicted Values by Group
In order to determine the range on which the trends separate significantly, the PLM procedure is executed in the following
statements with an ESTIMATE statement that applies group comparisons at a number of values for the spline variable x:
%macro GroupDiff;
%do x=0 %to 75 %by 5;
"Diff at x=&x" group 1 -1 group*spl [1,1 &x] [-1,2 &x],
%end;
'Diff at x=80' group 1 -1 group*spl [1,1 80] [-1,2 80]
%mend;
proc plm restore=ortho_spline;
show effects;
estimate %GroupDiff / adjust=simulate seed=1 stepdown;
run;
For example, the following ESTIMATE statement compares the trends between the two groups at x = 25:
estimate 'Diff at x=25' group 1 -1 group*spl [1,1 25] [-1,2 25];
The nonpositional syntax is used for the group*spl effect. For example, the specification ![]() requests that the spline be computed at x = 25 for the second level of variable
requests that the spline be computed at x = 25 for the second level of variable group. The resulting coefficients are added to the vector for the estimate after being multiplied with –1.
Because comparisons are made at a large number of values for x, a multiplicity correction is in order to adjust the p-values to reflect familywise error control. Simulated p-values with step-down adjustment are used here.
Output 69.6.3 displays the “Store Information” for the item store and information about the spline effect (the result of the SHOW statement).
Output 69.6.3: Spline Details
| B-splines Comparisons |
| Store Information | |
|---|---|
| Item Store | WORK.ORTHO_SPLINE |
| Data Set Created From | WORK.SPLINE |
| Created By | PROC ORTHOREG |
| Date Created | 13JUN12:12:38:57 |
| Response Variable | y |
| Class Variable | group |
| Constructed Effect | spl |
| Model Effects | group spl*group |
| B-splines Comparisons |
| Knots for Spline Effect spl | ||
|---|---|---|
| Knot Number | Boundary | x |
| 1 | * | -48.50000 |
| 2 | * | -23.75000 |
| 3 | * | 1.00000 |
| 4 | 25.75000 | |
| 5 | 50.50000 | |
| 6 | 75.25000 | |
| 7 | * | 100.00000 |
| 8 | * | 124.75000 |
| 9 | * | 149.50000 |
| B-splines Comparisons |
| Basis Details for Spline Effect spl | |||
|---|---|---|---|
| Column | Support | Support Knots | |
| 1 | -48.50000 | 25.75000 | 1-4 |
| 2 | -48.50000 | 50.50000 | 1-5 |
| 3 | -23.75000 | 75.25000 | 2-6 |
| 4 | 1.00000 | 100.00000 | 3-7 |
| 5 | 25.75000 | 124.75000 | 4-8 |
| 6 | 50.50000 | 149.50000 | 5-9 |
| 7 | 75.25000 | 149.50000 | 6-9 |
Output 69.6.4 displays the results from the ESTIMATE statement.
Output 69.6.4: Estimate Results with Multiplicity Correction
| Estimates Adjustment for Multiplicity: Holm-Simulated |
||||||
|---|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| Diff at x=0 | 12.4124 | 4.2130 | 86 | 2.95 | 0.0041 | 0.0206 |
| Diff at x=5 | 1.0376 | 0.1759 | 86 | 5.90 | <.0001 | <.0001 |
| Diff at x=10 | 0.3778 | 0.1540 | 86 | 2.45 | 0.0162 | 0.0545 |
| Diff at x=15 | 0.05822 | 0.1481 | 86 | 0.39 | 0.6952 | 0.9101 |
| Diff at x=20 | -0.02602 | 0.1243 | 86 | -0.21 | 0.8346 | 0.9565 |
| Diff at x=25 | 0.02014 | 0.1312 | 86 | 0.15 | 0.8783 | 0.9565 |
| Diff at x=30 | 0.1023 | 0.1378 | 86 | 0.74 | 0.4600 | 0.7418 |
| Diff at x=35 | 0.1924 | 0.1236 | 86 | 1.56 | 0.1231 | 0.2925 |
| Diff at x=40 | 0.2883 | 0.1114 | 86 | 2.59 | 0.0113 | 0.0450 |
| Diff at x=45 | 0.3877 | 0.1195 | 86 | 3.24 | 0.0017 | 0.0096 |
| Diff at x=50 | 0.4885 | 0.1308 | 86 | 3.74 | 0.0003 | 0.0024 |
| Diff at x=55 | 0.5903 | 0.1231 | 86 | 4.79 | <.0001 | <.0001 |
| Diff at x=60 | 0.7031 | 0.1125 | 86 | 6.25 | <.0001 | <.0001 |
| Diff at x=65 | 0.8401 | 0.1203 | 86 | 6.99 | <.0001 | <.0001 |
| Diff at x=70 | 1.0147 | 0.1348 | 86 | 7.52 | <.0001 | <.0001 |
| Diff at x=75 | 1.2400 | 0.1326 | 86 | 9.35 | <.0001 | <.0001 |
| Diff at x=80 | 1.5237 | 0.1281 | 86 | 11.89 | <.0001 | <.0001 |
Notice that the “Store Information” in Output 69.6.3 displays the classification variables (from the CLASS statement in PROC ORTHOREG), the constructed effects (from the EFFECT
statement in PROC ORTHOREG), and the model effects (from the MODEL statement in PROC ORTHOREG). Output 69.6.4 shows that at the 5% significance level the trends are significantly different for ![]() and for
and for ![]() . Between those values you cannot reject the hypothesis of trend congruity.
. Between those values you cannot reject the hypothesis of trend congruity.
To see this effect more clearly, you can filter the results by adding the a filtering statement to the previous PROC PLM step:
proc plm restore=ortho_spline; estimate %GroupDiff / adjust=simulate seed=1 stepdown; filter adjp > 0.05; run;
This produces Output 69.6.5, which displays the subset of the results in Output 69.6.4 that meets the condition in the FILTER expression.
Output 69.6.5: Filtered Estimate Results
| B-splines Comparisons |
| Estimates Adjustment for Multiplicity: Holm-Simulated |
||||||
|---|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| Diff at x=10 | 0.3778 | 0.1540 | 86 | 2.45 | 0.0162 | 0.0545 |
| Diff at x=15 | 0.05822 | 0.1481 | 86 | 0.39 | 0.6952 | 0.9101 |
| Diff at x=20 | -0.02602 | 0.1243 | 86 | -0.21 | 0.8346 | 0.9565 |
| Diff at x=25 | 0.02014 | 0.1312 | 86 | 0.15 | 0.8783 | 0.9565 |
| Diff at x=30 | 0.1023 | 0.1378 | 86 | 0.74 | 0.4600 | 0.7418 |
| Diff at x=35 | 0.1924 | 0.1236 | 86 | 1.56 | 0.1231 | 0.2925 |
