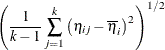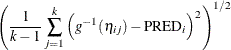The PLM Procedure

SCORE Statement

SCORE DATA=SAS-data-set <OUT=SAS-data-set><keyword<=name>> …<keyword<=name>> </ options> ;

The SCORE statement applies the contents of the source item store to compute predicted values and other observation-wise statistics for a SAS data set.

You can specify the following syntax elements in the SCORE statement before the option slash (/):

DATA=SAS-data-set

specifies the input data set for scoring. This option is required, and the data set is examined for congruity with the previously fitted (and stored) model. For example, all necessary variables to form a row of the $\bX$ matrix must be present in the input data set and must be of the correct type and format. The following variables do not have to be present in the input data set:

the response variable
the events and trials variables used in the events/trials syntax for binomial data
variables used in WEIGHT or FREQ statements

OUT=SAS-data-set

specifies the name of the output data set. If you do not specify an output data set with the OUT= option, the PLM procedure uses the DATAn convention to name the output data set.

keyword<=name>

specifies a statistic to be included in the OUT= data set and optionally assigns the statistic the variable name name. Table 69.9 lists the keywords and the default names assigned by the PLM procedure if you do not specify a name.

Table 69.9: Keywords for Output Statistics

Keyword	Description	Expression	Name
PREDICTED	Linear predictor	$\widehat{\eta } = \mb {x}\widehat{\bbeta }$	Predicted
STDERR	Standard deviation of linear predictor	$\sqrt {\mr {Var}(\widehat{\eta })}$	StdErr
RESIDUAL	Residual	$y - g^{-1}(\widehat{\eta })$	Resid
LCLM	Lower confidence limit for the linear predictor		LCLM
UCLM	Upper confidence limit for the linear predictor		UCLM
LCL	Lower prediction limit for the linear predictor		LCL
UCL	Upper prediction limit for the linear predictor		UCL

Prediction limits (LCL, UCL) are available only for statistical models that allow such limits, typically regression-type models for normally distributed data with an identity link function.

You can specify the following options in the SCORE statement after a slash (/):

ALPHA=number

determines the coverage probability for two-sided confidence and prediction intervals. The coverage probability is computed as 1 – number. The value of number must be between 0 and 1; the default is 0.05.

DF=number

specifies the degrees of freedom to use in the construction of prediction and confidence limits.

ILINK

requests that predicted values be inversely linked to produce predictions on the data scale. By default, predictions are produced on the linear scale where covariate effects are additive.

NOUNIQUE

requests that names not be made unique in the case of naming conflicts. By default, the PLM procedure avoids naming conflicts by assigning a unique name to each output variable. If you specify the NOUNIQUE option, variables with conflicting names are not renamed. In that case, the first variable added to the output data set takes precedence.

NOVAR

requests that variables from the input data set not be added to the output data set.

OBSCAT

requests that statistics in models for multinomial data be written to the output data set only for the response level that corresponds to the observed level of the observation.

SAMPLE

requests that the sample of parameter estimates in the item store be used to form scoring statistics. This option is useful when the item store contains the results of a Bayesian analysis and a posterior sample of parameter estimates. The predicted value is then computed as the average predicted value across the posterior estimates, and the standard error measures the standard deviation of these estimates. For example, let $\widehat{\bbeta }_1, \ldots , \widehat{\bbeta }_ k$ denote the k posterior sample estimates of $\bbeta$ , and let $\mb {x}_ i$ denote the x-vector for the ith observation in the scoring data set. If the SAMPLE option is in effect, the output statistics for the predicted value, the standard error, and the residual of the ith observation are computed as

$\displaystyle \eta _{ij}$	$\displaystyle =$	$\displaystyle \mb {x}_ i\widehat{\bbeta }_ j$
$\displaystyle \mr {PRED}_ i$	$\displaystyle =$	$\displaystyle \overline{\eta }_ i = \frac{1}{k} \sum _{j=1}^{k}\eta _{ij}$
$\displaystyle \mr {STDERR}_ i$	$\displaystyle =$	$\displaystyle \left( \frac{1}{k-1} \sum _{j=1}^{k} \left(\eta _{ij} - \overline{\eta }_ i\right)^2 \right)^{1/2}$
$\displaystyle \mr {RESIDUAL}_ i$	$\displaystyle =$	$\displaystyle y_ i - g^{-1}\left(\overline{\eta }_ i\right)$

where $g^{-1}(\cdot )$ denotes the inverse link function.

If, in addition, the ILINK option is in effect, the calculations are as follows:

$\displaystyle \eta _{ij}$	$\displaystyle =$	$\displaystyle \mb {x}_ i\widehat{\bbeta }_ j$
$\displaystyle \mr {PRED}_ i$	$\displaystyle =$	$\displaystyle \frac{1}{k} \sum _{j=1}^{k} g^{-1}\left(\eta _{ij}\right)$
$\displaystyle \mr {STDERR}_ i$	$\displaystyle =$	$\displaystyle \left( \frac{1}{k-1} \sum _{j=1}^{k} \left(g^{-1}(\eta _{ij}) - \mr {PRED}_ i \right)^2 \right)^{1/2}$
$\displaystyle \mr {RESIDUAL}_ i$	$\displaystyle =$	$\displaystyle y_ i - \mr {PRED}_ i$

The LCL and UCL statistics are not available with the SAMPLE option. When the LCLM and UCLM statistics are requested, the SAMPLE option yields the lower $100 \times \alpha /2$ % and upper $100 \times (1-\alpha /2)$ % percentiles of the predicted values under the sample (posterior) distribution. When you request residuals with the SAMPLE option, the calculation depends on whether the ILINK option is specified.