The POWER Procedure

Agresti, A. (1980), “Generalized Odds Ratios for Ordinal Data,” Biometrics, 36, 59–67.

Agresti, A. and Coull, B. A. (1998), “Approximate is Better Than 'Exact' for Interval Estimation of Binomial Proportions,” The American Statistician, 52, 119–126.

Anderson, T. W. (1984), An Introduction to Multivariate Statistical Analysis, Second Edition, New York: John Wiley & Sons.

Beal, S. L. (1989), “Sample Size Determination for Confidence Intervals on the Population Means and on the Difference between Two Population Means,” Biometrics, 45, 969–977.

Blackwelder, W. C. (1982), “'Proving the Null Hypothesis' in Clinical Trials,” Controlled Clinical Trials, 3, 345–353.

Brown, L. D., Cai, T. T., and DasGupta, A. (2001), “Interval Estimation for a Binomial Proportion,” Statistical Science, 16, 101–133.

Cantor, A. B. (1997), Extending SAS Survival Analysis Techniques for Medical Research, Cary, NC: SAS Press.

Castelloe, J. M. (2000), “Sample Size Computations and Power Analysis with the SAS System,” in Proceedings of the Twenty-fifth Annual SAS Users Group International Conference, Cary, NC: SAS Institute Inc.

Castelloe, J. M. and O’Brien, R. G. (2001), “Power and Sample Size Determination for Linear Models,” in Proceedings of the Twenty-sixth Annual SAS Users Group International Conference, Cary, NC: SAS Institute Inc.

Chernick, M. R. and Liu, C. Y. (2002), “The Saw-Toothed Behavior of Power Versus Sample Size and Software Solutions: Single Binomial Proportion Using Exact Methods,” The American Statistician, 56, 149–155.

Chow, S.-C., Shao, J., and Wang, H. (2003), Sample Size Calculations in Clinical Research, Boca Raton, FL: CRC Press.

Connor, R. J. (1987), “Sample Size for Testing Differences in Proportions for the Paired-Sample Design,” Biometrics, 43, 207–211.

Diegert, C. and Diegert, K. V. (1981), “Note on Inversion of Casagrande-Pike-Smith Approximate Sample-Size Formula for Fisher-Irwin Test on 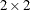Tables,” Biometrics, 37, 595.

Diletti, D., Hauschke, D., and Steinijans, V. W. (1991), “Sample Size Determination for Bioequivalence Assessment by Means of Confidence Intervals,” International Journal of Clinical Pharmacology, Therapy and Toxicology, 29, 1–8.

DiSantostefano, R. L. and Muller, K. E. (1995), “A Comparison of Power Approximations for Satterthwaite’s Test,” Communications in Statistics—Simulation and Computation, 24, 583–593.

Fisher, R. A. (1921), “On the 'Probable Error' of a Coefficient of Correlation Deduced from a Small Sample,” Metron, 1, 3–32.

Fleiss, J. L., Tytun, A., and Ury, H. K. (1980), “A Simple Approximation for Calculating Sample Sizes for Comparing Independent Proportions,” Biometrics, 36, 343–346.

Gatsonis, C. and Sampson, A. R. (1989), “Multiple Correlation: Exact Power and Sample Size Calculations,” Psychological Bulletin, 106, 516–524.

Hocking, R. R. (1985), The Analysis of Linear Models, Belmont, CA: Brooks/Cole.

Hsieh, F. Y. (1989), “Sample Size Tables for Logistic Regression,” Statistics in Medicine, 8, 795–802.

Johnson, N. L. and Kotz, S. (1970), Distributions in Statistics: Continuous Univariate Distributions — 1, New York: John Wiley & Sons.

Johnson, N. L., Kotz, S., and Balakrishnan, N. (1994), Continuous Univariate Distributions, volume 1, Second Edition, New York: John Wiley & Sons.

Johnson, N. L., Kotz, S., and Balakrishnan, N. (1995), Continuous Univariate Distributions, volume 2, Second Edition, New York: John Wiley & Sons.

Johnson, N. L., Kotz, S., and Kemp, A. W. (1992), Univariate Discrete Distributions, Second Edition, New York: John Wiley & Sons.

Jones, R. M. and Miller, K. S. (1966), “On the Multivariate Lognormal Distribution,” Journal of Industrial Mathematics, 16, 63–76.

Kolassa, J. E. (1995), “A Comparison of Size and Power Calculations for the Wilcoxon Statistic for Ordered Categorical Data,” Statistics in Medicine, 14, 1577–1581.

Lachin, J. M. (1992), “Power and Sample Size Evaluation for the McNemar Test with Application to Matched Case-Control Studies,” Statistics in Medicine, 11, 1239–1251.

Lakatos, E. (1988), “Sample Sizes Based on the Log-Rank Statistic in Complex Clinical Trials,” Biometrics, 44, 229–241.

Lenth, R. V. (2001), “Some Practical Guidelines for Effective Sample Size Determination,” The American Statistician, 55, 187–193.

Maxwell, S. E. (2000), “Sample Size and Multiple Regression Analysis,” Psychological Methods, 5, 434–458.

Miettinen, O. S. (1968), “The Matched Pairs Design in the Case of All-or-None Responses,” Biometrics, 24, 339–352.

Moser, B. K., Stevens, G. R., and Watts, C. L. (1989), “The Two-Sample T Test versus Satterthwaite’s Approximate F Test,” Communications in Statistics A—Theory and Methods, 18, 3963–3975.

Muller, K. E. and Benignus, V. A. (1992), “Increasing Scientific Power with Statistical Power,” Neurotoxicology and Teratology, 14, 211–219.

O’Brien, R. G. and Castelloe, J. (2007), “Sample-Size Analysis for Traditional Hypothesis Testing: Concepts and Issues,” in A. Dmitrienko, C. Chuang-Stein, and R. D’Agostino, eds., Pharmaceutical Statistics Using SAS: A Practical Guide, 237–271, Cary, NC: SAS Institute Inc.

O’Brien, R. G. and Castelloe, J. M. (2006), “Exploiting the Link between the Wilcoxon-Mann-Whitney Test and a Simple Odds Statistic,” in Proceedings of the Thirty-First Annual SAS Users Group International Conference, Cary, NC: SAS Institute Inc, paper 209-31.

O’Brien, R. G. and Muller, K. E. (1993), “Unified Power Analysis for t-Tests through Multivariate Hypotheses,” in L. K. Edwards, ed., Applied Analysis of Variance in Behavioral Science, 297–344, New York: Marcel Dekker.

Owen, D. B. (1965), “A Special Case of a Bivariate Non-central t-Distribution,” Biometrika, 52, 437–446.

Pagano, M. and Gauvreau, K. (1993), Principles of Biostatistics, Belmont, CA: Wadsworth.

Phillips, K. F. (1990), “Power of the Two One-Sided Tests Procedure in Bioequivalence,” Journal of Pharmacokinetics and Biopharmaceutics, 18, 137–144.

Satterthwaite, F. E. (1946), “An Approximate Distribution of Estimates of Variance Components,” Biometrics Bulletin, 2, 110–114.

Schork, M. and Williams, G. (1980), “Number of Observations Required for the Comparison of Two Correlated Proportions,” Communications in Statistics—Simulation and Computation, 9, 349–357.

Schuirmann, D. J. (1987), “A Comparison of the Two One-Sided Tests Procedure and the Power Approach for Assessing the Equivalence of Average Bioavailability,” Journal of Pharmacokinetics and Biopharmaceutics, 15, 657–680.

Self, S. G., Mauritsen, R. H., and Ohara, J. (1992), “Power Calculations for Likelihood Ratio Tests in Generalized Linear Models,” Biometrics, 48, 31–39.

Senn, S. (1993), Cross-over Trials in Clinical Research, New York: John Wiley & Sons.

Shieh, G. (2000), “A Comparison of Two Approaches for Power and Sample Size Calculations in Logistic Regression Models,” Communications in Statistics—Simulation, 29, 763–791.

Shieh, G. and O’Brien, R. G. (1998), “A Simpler Method to Compute Power for Likelihood Ratio Tests in Generalized Linear Models,” in Annual Joint Statistical Meetings of the American Statistical Association, Dallas: American Statistical Association.

Stuart, A. and Ord, J. K. (1994), Kendall’s Advanced Theory of Statistics, Volume 1: Distribution Theory, 6 Edition, Baltimore: Edward Arnold Publishers.

Walters, D. E. (1979), “In Defence of the Arc Sine Approximation,” The Statistician, 28, 219–232.

Wellek, S. (2003), Testing Statistical Hypotheses of Equivalence, Boca Raton, FL: Chapman & Hall/CRC Press LLC.