The POWER Procedure
- Overview
-
Getting Started

-
Syntax

-
Details

-
Examples
 One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test
One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test - References
MULTREG Statement
MULTREG <options> ;
The MULTREG statement performs power and sample size analyses for Type III F tests of sets of predictors in multiple linear regression, assuming either fixed or normally distributed predictors.
Summary of Options
Table 71.4 summarizes the options available in the MULTREG statement.
Table 71.4: MULTREG Statement Options
|
Option |
Description |
|---|---|
|
Define analysis |
|
|
Specifies the statistical analysis |
|
|
Specify analysis information |
|
|
Specifies the significance level |
|
|
Specifies the assumed distribution of the predictors |
|
|
Specifies the number of predictors in the full model |
|
|
Specifies a no-intercept model |
|
|
Specifies the number of predictors in the reduced model |
|
|
Specifies the number of predictors being tested |
|
|
Specify effects |
|
|
Specifies the partial correlation |
|
|
Specifies the difference in |
|
|
Specifies the |
|
|
Specifies the |
|
|
Specify sample size |
|
|
Enables fractional input and output for sample sizes |
|
|
Specifies the sample size |
|
|
Specify power |
|
|
Specifies the desired power |
|
|
Control ordering in output |
|
|
Controls the order of parameters |
|
Table 71.5 summarizes the valid result parameters in the MULTREG statement.
Table 71.5: Summary of Result Parameters in the MULTREG Statement
Dictionary of Options
Restrictions on Option Combinations
To specify the number of predictors, use any two of these three options:
-
the number of predictors in the full model (NFULLPREDICTORS=)
-
the number of predictors in the reduced model (NREDUCEDPREDICTORS=)
-
the number of predictors being tested (NTESTPREDICTORS=)
To specify the effect, choose one of the following parameterizations:
-
partial correlation (by using the PARTIALCORR= option)
-
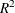 for the full and reduced models (by using any two of RSQUAREDIFF=, RSQUAREFULL=, and RSQUAREREDUCED=)
for the full and reduced models (by using any two of RSQUAREDIFF=, RSQUAREFULL=, and RSQUAREREDUCED=)
Option Groups for Common Analyses
This section summarizes the syntax for the common analyses supported in the MULTREG statement.
Type III F Test of a Set of Predictors
You can express effects in terms of partial correlation, as in the following statements. Default values of the TEST=, MODEL=, and ALPHA= options specify a Type III F test with a significance level of 0.05, assuming normally distributed predictors.
proc power;
multreg
model = random
nfullpredictors = 7
ntestpredictors = 3
partialcorr = 0.35
ntotal = 100
power = .;
run;
You can also express effects in terms of ![]() :
:
proc power;
multreg
model = fixed
nfullpredictors = 7
ntestpredictors = 3
rsquarefull = 0.9
rsquarediff = 0.1
ntotal = .
power = 0.9;
run;