The ROBUSTREG Procedure
M Estimation
This example shows how you can use the ROBUSTREG procedure to do M estimation, which is a commonly used method for outlier detection and robust regression when contamination is mainly in the response direction.
data stack; input x1 x2 x3 y exp $ @@; datalines; 80 27 89 42 e1 80 27 88 37 e2 75 25 90 37 e3 62 24 87 28 e4 62 22 87 18 e5 62 23 87 18 e6 62 24 93 19 e7 62 24 93 20 e8 58 23 87 15 e9 58 18 80 14 e10 58 18 89 14 e11 58 17 88 13 e12 58 18 82 11 e13 58 19 93 12 e14 50 18 89 8 e15 50 18 86 7 e16 50 19 72 8 e17 50 19 79 8 e18 50 20 80 9 e19 56 20 82 15 e20 70 20 91 15 e21 ;
The data set stack is the well-known stack-loss data set presented by Brownlee (1965). The data describe the operation of a plant for the oxidation of ammonia to nitric acid and consist of 21 four-dimensional
observations. The explanatory variables for the response stack-loss (y) are the rate of operation (x1), the cooling water inlet temperature (x2), and the acid concentration (x3).
The following ROBUSTREG statements analyze the data:
proc robustreg data=stack; model y = x1 x2 x3 / diagnostics leverage; id exp; test x3; run;
By default, the procedure does M estimation with the bisquare weight function, and it uses the median method for estimating
the scale parameter. The MODEL statement specifies the covariate effects. The DIAGNOSTICS option requests a table for outlier
diagnostics, and the LEVERAGE option adds leverage-point diagnostic results to this table for continuous covariate effects.
The ID statement specifies that the variable exp is used to identify each observation (experiment) in this table. If the ID statement is omitted, the observation number is
used to identify the observations. The TEST statement requests a test of significance for the covariate effects specified.
The results of this analysis are displayed in the following figures.
Figure 80.1: Model Fitting Information and Summary Statistics
| Model Information | |
|---|---|
| Data Set | WORK.STACK |
| Dependent Variable | y |
| Number of Independent Variables | 3 |
| Number of Observations | 21 |
| Method | M Estimation |
| Summary Statistics | ||||||
|---|---|---|---|---|---|---|
| Variable | Q1 | Median | Q3 | Mean | Standard Deviation |
MAD |
| x1 | 53.0000 | 58.0000 | 62.0000 | 60.4286 | 9.1683 | 5.9304 |
| x2 | 18.0000 | 20.0000 | 24.0000 | 21.0952 | 3.1608 | 2.9652 |
| x3 | 82.0000 | 87.0000 | 89.5000 | 86.2857 | 5.3586 | 4.4478 |
| y | 10.0000 | 15.0000 | 19.5000 | 17.5238 | 10.1716 | 5.9304 |
Figure 80.1 displays the model fitting information and summary statistics for the response variable and the continuous covariates. The
columns labeled Q1, Median, and Q3 provide the lower quantile, median, and upper quantile, respectively. The column labeled
MAD provides a robust estimate of the univariate scale, which is computed as the standardized median absolute deviation (MAD).
See Huber (1981, p. 108) for more details about the standardized MAD. The columns labeled Mean and Standard Deviation provide the usual mean
and standard deviation. A large difference between the standard deviation and the MAD for a variable indicates some extreme
values for this variable. In the stack-loss data, the stack-loss (response y) has the biggest difference between the standard deviation and the MAD.
Figure 80.2: Model Parameter Estimates
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | Chi-Square | Pr > ChiSq | |
| Intercept | 1 | -42.2854 | 9.5045 | -60.9138 | -23.6569 | 19.79 | <.0001 |
| x1 | 1 | 0.9276 | 0.1077 | 0.7164 | 1.1387 | 74.11 | <.0001 |
| x2 | 1 | 0.6507 | 0.2940 | 0.0744 | 1.2270 | 4.90 | 0.0269 |
| x3 | 1 | -0.1123 | 0.1249 | -0.3571 | 0.1324 | 0.81 | 0.3683 |
| Scale | 1 | 2.2819 | |||||
Figure 80.2 displays the table of robust parameter estimates, standard errors, and confidence limits. The row labeled Scale provides a point estimate of the scale parameter in the linear regression model, which is obtained by the median method. See the section M Estimation for more information about scale estimation methods. For the stack-loss data, M estimation yields the fitted linear model:
|
|
Figure 80.3: Diagnostics
| Diagnostics | ||||||
|---|---|---|---|---|---|---|
| Obs | exp | Mahalanobis Distance | Robust MCD Distance | Leverage | Standardized Robust Residual |
Outlier |
| 1 | e1 | 2.2536 | 5.5284 | * | 1.0995 | |
| 2 | e2 | 2.3247 | 5.6374 | * | -1.1409 | |
| 3 | e3 | 1.5937 | 4.1972 | * | 1.5604 | |
| 4 | e4 | 1.2719 | 1.5887 | 3.0381 | * | |
| 21 | e21 | 2.1768 | 3.6573 | * | -4.5733 | * |
Figure 80.3 displays outlier and leverage-point diagnostics. Standardized robust residuals are computed based on the estimated parameters. Both the Mahalanobis distance and the robust MCD distance are displayed. Outliers and leverage points, identified with asterisks, are defined by the standardized robust residuals and robust MCD distances that exceed the corresponding cutoff values displayed in the diagnostics summary. Observations 4 and 21 are outliers because their standardized robust residuals exceed the cutoff value in absolute value. The procedure detects four observations with high leverage. Leverage points (points with high leverage) with smaller standardized robust residuals than the cutoff value in absolute value are called good leverage points; others are called bad leverage points. Observation 21 is a bad leverage point.
Two particularly useful plots for revealing outliers and leverage points are a scatter plot of the standardized robust residuals against the robust distances (RDPLOT) and a scatter plot of the robust distances against the classical Mahalanobis distances (DDPLOT).
For the stack-loss data, the following statements produce the RDPLOT in Figure 80.4 and the DDPLOT in Figure 80.5. The histogram and the normal quantile-quantile plots (shown in Figure 80.6 and Figure 80.7, respectively) for the standardized robust residuals are also created with the HISTOGRAM and QQPLOT suboptions of the PLOTS= option.
ods graphics on; proc robustreg data=stack plots=(rdplot ddplot histogram qqplot); model y = x1 x2 x3; run; ods graphics off;
These plots are helpful in identifying outliers in addition to good and bad high leverage points.
These plots are requested when ODS Graphics is enabled by specifying the PLOTS= option in the PROC ROBUSTREG statement. For general information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS. For specific information about the graphics available in the ROBUSTREG procedure, see the section ODS Graphics.
Figure 80.4: RDPLOT for Stackloss Data
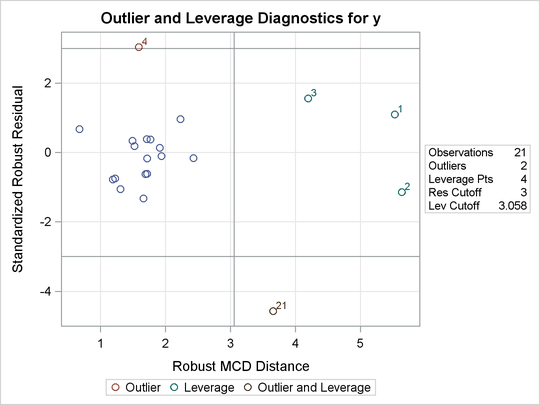
Figure 80.5: DDPLOT for Stackloss Data
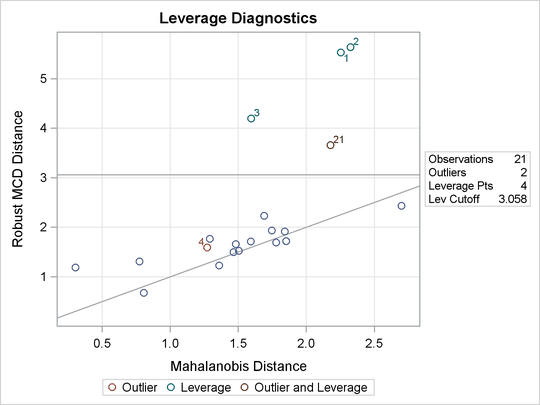
Figure 80.6: Histogram
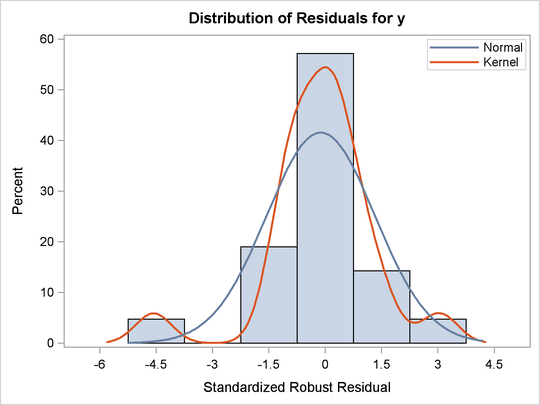
Figure 80.7: Q-Q Plot
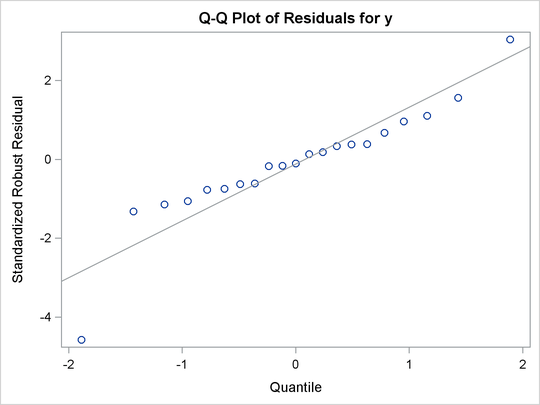
Figure 80.8 displays robust versions of goodness-of-fit statistics for the model. You can use the robust information criteria, AICR and BICR, for model selection and comparison. For both AICR and BICR, the lower the value, the more desirable the model.
Figure 80.8: Goodness-of-Fit Statistics
| Goodness-of-Fit | |
|---|---|
| Statistic | Value |
| R-Square | 0.6659 |
| AICR | 29.5231 |
| BICR | 36.3361 |
| Deviance | 125.7905 |
Figure 80.9 displays the test results requested by the TEST statement. The ROBUSTREG procedure conducts two robust linear tests, the
![]() test and the
test and the ![]() test. See the section Linear Tests for information about how the procedure computes test statistics and the correction factor lambda. Due to the large p-values for both tests, you can conclude that the effect
test. See the section Linear Tests for information about how the procedure computes test statistics and the correction factor lambda. Due to the large p-values for both tests, you can conclude that the effect x3 is not significant at the 5% level.
Figure 80.9: Test of Significance
| Robust Linear Test | |||||
|---|---|---|---|---|---|
| Test | Test Statistic | Lambda | DF | Chi-Square | Pr > ChiSq |
| Rho | 0.9378 | 0.7977 | 1 | 1.18 | 0.2782 |
| Rn2 | 0.8092 | 1 | 0.81 | 0.3683 | |
For the bisquare weight function, the default tuning constant, c = 4.685, is chosen to yield a 95% asymptotic efficiency of the M estimates with the Gaussian distribution. See the section M Estimation for details. The smaller the constant c, the lower the asymptotic efficiency but the sharper the M estimate as an outlier detector. For the stack-loss data set, you could consider using a sharper outlier detector.
In the following PROC ROBUSTREG step, a smaller constant, c = 3.5, is used. This tuning constant corresponds to an efficiency close to 85%. See Chen and Yin (2002) for the relationship between the tuning constant and asymptotic efficiency of M estimates.
proc robustreg method=m(wf=bisquare(c=3.5)) data=stack; model y = x1 x2 x3 / diagnostics leverage; id exp; test x3; run;
Figure 80.10 displays the table of robust parameter estimates, standard errors, and confidence limits with the constant c = 3.5.
The refitted linear model is
|
|
Figure 80.10: Model Parameter Estimates
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | Chi-Square | Pr > ChiSq | |
| Intercept | 1 | -37.1076 | 5.4731 | -47.8346 | -26.3805 | 45.97 | <.0001 |
| x1 | 1 | 0.8191 | 0.0620 | 0.6975 | 0.9407 | 174.28 | <.0001 |
| x2 | 1 | 0.5173 | 0.1693 | 0.1855 | 0.8492 | 9.33 | 0.0022 |
| x3 | 1 | -0.0728 | 0.0719 | -0.2138 | 0.0681 | 1.03 | 0.3111 |
| Scale | 1 | 1.4265 | |||||
Figure 80.11 displays outlier and leverage-point diagnostics with the constant c = 3.5. Besides observations 4 and 21, observations 1 and 3 are also detected as outliers.
Figure 80.11: Diagnostics
| Diagnostics | ||||||
|---|---|---|---|---|---|---|
| Obs | exp | Mahalanobis Distance | Robust MCD Distance | Leverage | Standardized Robust Residual |
Outlier |
| 1 | e1 | 2.2536 | 5.5284 | * | 4.2719 | * |
| 2 | e2 | 2.3247 | 5.6374 | * | 0.7158 | |
| 3 | e3 | 1.5937 | 4.1972 | * | 4.4142 | * |
| 4 | e4 | 1.2719 | 1.5887 | 5.7792 | * | |
| 21 | e21 | 2.1768 | 3.6573 | * | -6.2727 | * |
