The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data - References
Summary of Methods in Group Sequential Designs
There are three different types of methods available in the SEQDESIGN procedure: fixed boundary shape methods for specified boundary shape, Whitehead methods for boundaries from continuous monitoring, and error spending methods for specified error spending at each stage.
The fixed boundary shape methods include unified family methods and Haybittle-Peto methods. The unified family methods include Pocock, O’Brien-Fleming, power family, and triangular methods.
Pocock Method
Pocock derives the constant boundary on the standardized Z scale to demonstrate the sequential design while maintaining the overall ![]() and
and ![]() levels (Pocock, 1977). The resulting boundary tends to stop the trials early with a larger p-value. This boundary is commonly called a Pocock boundary, but Pocock himself does not advocate these boundary values for
stopping a trial early to reject the null hypothesis, because large p-values might not be persuasive enough (Pocock and White, 1999). Also, the nominal p-value at the final stage is much smaller than the overall p-value of the design. That is, the trial might stop at the final stage with a small nominal p-value, but the test is not rejected, which might not be easy to justify.
levels (Pocock, 1977). The resulting boundary tends to stop the trials early with a larger p-value. This boundary is commonly called a Pocock boundary, but Pocock himself does not advocate these boundary values for
stopping a trial early to reject the null hypothesis, because large p-values might not be persuasive enough (Pocock and White, 1999). Also, the nominal p-value at the final stage is much smaller than the overall p-value of the design. That is, the trial might stop at the final stage with a small nominal p-value, but the test is not rejected, which might not be easy to justify.
O’Brien-Fleming Method
O’Brien-Fleming boundary values are inversely proportional to the square root of information levels on the standardized Z scale (O’Brien and Fleming, 1979). The O’Brien-Fleming boundary is conservative in the early stages and tends to stop the trials early only with a small p-value. But the nominal value at the final stage is close to the overall p-value of the design.
Power Family Method
The power family method (Wang and Tsiatis, 1987; Emerson and Fleming, 1989; Pampallona and Tsiatis, 1994) generalizes the Pocock and O’Brien-Fleming methods with a power parameter to allow continuous movement between the Pocock
and O’Brien-Fleming methods. The power parameter is ![]() for the Pocock method and
for the Pocock method and ![]() for the O’Brien-Fleming method.
for the O’Brien-Fleming method.
Triangular Method
The unified family triangular method (Kittelson and Emerson, 1999) contains straight-line boundaries on the score scale. For a one-sided trial with early stopping either to reject and to
accept the null hypothesis, the method produces a triangular continuation region. The boundary shape is specified with the
slope parameter ![]() .
.
Unified Family Method
The unified family method (Kittelson and Emerson, 1999) extends power family methods to incorporate the triangular method, which contains straight-line boundaries on the score scale.
Haybittle-Peto Method
The Haybittle-Peto method (Haybittle, 1971; Peto et al., 1976) uses a Z value of 3 for the critical values in interim stages and derives the critical value at the final stage. With this method, the final-stage critical value is close to the original design without interim monitoring. The SEQDESIGN procedure extends this method further to allow for different Z or nominal p-values for the boundaries.
Whitehead Method
Whitehead methods (Whitehead and Stratton, 1983; Whitehead, 1997, 2001) derive the boundary values by adapting the continuous monitoring tests to the discrete monitoring of group sequential tests. With early stopping to reject or accept the null hypothesis in a one-sided test, the derived continuation region has a triangular shape on the score-scaled boundaries. Only elementary calculations are needed to derive the boundary values in Whitehead’s triangular methods. The resulting Type I error probability and power are extremely close but differ slightly from the specified values due to the approximations used in deriving the tests (Jennison and Turnbull, 2000, p. 106). The SEQDESIGN procedure provides the BOUNDARYKEY= option to adjust the boundary value at the final stage for the exact Type I or Type II error probability levels.
Error Spending Method
The error spending method uses the specified ![]() and
and ![]() errors to be used at each stage of the design to derive the boundary values.
errors to be used at each stage of the design to derive the boundary values.
Error Spending Function Method
The error spending function method uses the error spending function to compute the ![]() and
and ![]() errors to be used at each stage of the design and then to derive the boundary values for these errors. The following four
error spending functions are available in the SEQDESIGN procedure:
errors to be used at each stage of the design and then to derive the boundary values for these errors. The following four
error spending functions are available in the SEQDESIGN procedure:
-
The Pocock-type error spending function (Lan and DeMets, 1983) produces boundaries similar to those produced with Pocock’s method.
-
The O’Brien-Fleming-type error spending function (Lan and DeMets, 1983) produces boundaries similar to those produced with the O’Brien-Fleming method.
-
The gamma error spending function (Hwang, Shih, and DeCani, 1990) specifies a gamma cumulative error spending function indexed by the gamma parameter
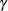 . The boundaries created with
. The boundaries created with 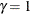 are similar to the boundaries from the Pocock method, and the boundaries created with
are similar to the boundaries from the Pocock method, and the boundaries created with 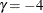 or
or 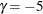 are similar to the boundaries from the O’Brien-Fleming method.
are similar to the boundaries from the O’Brien-Fleming method.
-
The power error spending function (Jennison and Turnbull, 2000, p. 148) specifies a power cumulative error spending function indexed by the power parameter
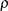 . The boundaries created with
. The boundaries created with 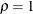 are similar to the boundaries from the Pocock method, and the boundaries created with
are similar to the boundaries from the Pocock method, and the boundaries created with 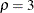 are similar to the boundaries from the O’Brien-Fleming method.
are similar to the boundaries from the O’Brien-Fleming method.