The TPSPLINE Procedure
Example 96.3 Multiple Minima of the GCV Function
The data in this example represent the deposition of sulfate (SO![]() ) at 179 sites in the 48 contiguous states of the United States in 1990. Each observation records the latitude and longitude
of the site in addition to the SO
) at 179 sites in the 48 contiguous states of the United States in 1990. Each observation records the latitude and longitude
of the site in addition to the SO![]() deposition at the site measured in grams per square meter (
deposition at the site measured in grams per square meter (![]() ).
).
You can use PROC TPSPLINE to fit a surface that reflects the general trend and that reveals underlying features of the data, which are shown in the following DATA step:
data so4; input latitude longitude so4 @@; datalines; 32.45833 87.24222 1.403 34.28778 85.96889 2.103 33.07139 109.86472 0.299 36.07167 112.15500 0.304 31.95056 112.80000 0.263 33.60500 92.09722 1.950 34.17944 93.09861 2.168 36.08389 92.58694 1.578 ... more lines ... 43.87333 104.19222 0.306 44.91722 110.42028 0.210 45.07611 72.67556 2.646 ;
data pred;
do latitude = 25 to 47 by 1;
do longitude = 68 to 124 by 1;
output;
end;
end;
run;
The preceding statements create the SAS data set so4 and the data set pred in order to make predictions on a regular grid. The following statements fit a surface for SO![]() deposition:
deposition:
ods graphics on; proc tpspline data=so4 plots(only)=criterion; model so4 = (latitude longitude) /lognlambda=(-6 to 1 by 0.1); score data=pred out=prediction1; run;
Partial output from these statements is displayed in Output 96.3.1 and Output 96.3.2.
Output 96.3.1: Partial Output from PROC TPSPLINE for Data Set SO![]()
| Raw Data |
| Summary of Input Data Set | |
|---|---|
| Number of Non-Missing Observations | 179 |
| Number of Missing Observations | 0 |
| Unique Smoothing Design Points | 179 |
| Summary of Final Model | |
|---|---|
| Number of Regression Variables | 0 |
| Number of Smoothing Variables | 2 |
| Order of Derivative in the Penalty | 2 |
| Dimension of Polynomial Space | 3 |
Output 96.3.2: Partial Output from PROC TPSPLINE for Data Set SO![]()
| Summary Statistics of Final Estimation | |
|---|---|
| log10(n*Lambda) | 0.2770 |
| Smoothing Penalty | 2.4588 |
| Residual SS | 12.4450 |
| Tr(I-A) | 140.2750 |
| Model DF | 38.7250 |
| Standard Deviation | 0.2979 |
| GCV | 0.1132 |
Output 96.3.3 displays the CriterionPlot of the GCV function versus ![]() .
.
Output 96.3.3: GCV Function of SO![]() Data Set
Data Set
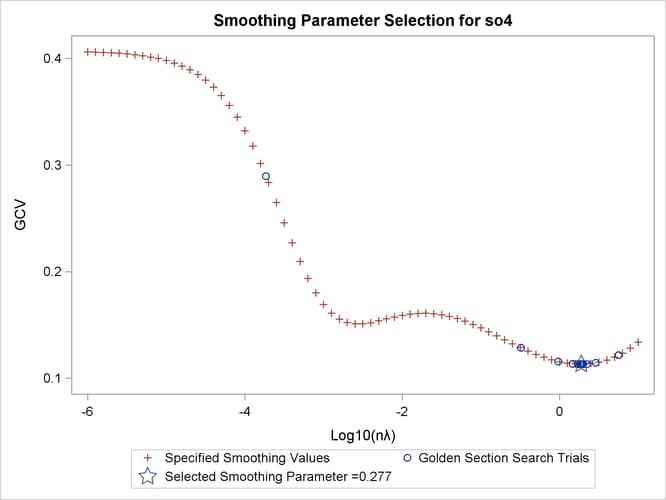
The GCV function has two minima. PROC TPSPLINE locates the global minimum at 0.277005. The plot also displays a local minimum
located around –2.56. The TPSPLINE procedure might not always find the global minimum, although it did in this case. If there
is a predetermined search range based on prior knowledge, you can use the RANGE= option to narrow the search range in order to find a desired smoothing value. For example, if you believe a better smoothing
parameter should be within the ![]() range, you can obtain the model with
range, you can obtain the model with ![]() with the following statements.
with the following statements.
proc tpspline data=so4; model so4 = (latitude longitude) / range=(-4,-2); score data=pred out=prediction2; run;
Output 96.3.4 displays the output from PROC TPSPLINE with a specified search range from the smoothing parameter.
Output 96.3.4: Output from PROC TPSPLINE for Data Set SO![]() with
with ![]()
| Raw Data |
| Summary of Input Data Set | |
|---|---|
| Number of Non-Missing Observations | 179 |
| Number of Missing Observations | 0 |
| Unique Smoothing Design Points | 179 |
| Summary of Final Model | |
|---|---|
| Number of Regression Variables | 0 |
| Number of Smoothing Variables | 2 |
| Order of Derivative in the Penalty | 2 |
| Dimension of Polynomial Space | 3 |
| Summary Statistics of Final Estimation | |
|---|---|
| log10(n*Lambda) | -2.5600 |
| Smoothing Penalty | 177.2160 |
| Residual SS | 0.0438 |
| Tr(I-A) | 7.2083 |
| Model DF | 171.7917 |
| Standard Deviation | 0.0779 |
| GCV | 0.1508 |
The smoothing penalty in Output 96.3.4 is much larger than that displayed in Output 96.3.2. The estimate in Output 96.3.2 uses a large ![]() value; therefore, the surface is smoother than the estimate by using
value; therefore, the surface is smoother than the estimate by using ![]() (Output 96.3.4).
(Output 96.3.4).
The estimate based on ![]() has a larger value of degrees of freedom, and it has a much smaller standard deviation.
has a larger value of degrees of freedom, and it has a much smaller standard deviation.
However, a smaller standard deviation in nonparametric regression does not necessarily mean that the estimate is good: a small
![]() value always produces an estimate closer to the data and, therefore, a smaller standard deviation.
value always produces an estimate closer to the data and, therefore, a smaller standard deviation.
When ODS Graphics is enabled, you can compare the two fits by supplying 0.277 and –2.56 to the LOGNLAMBDA= option:
proc tpspline data=so4; model so4 = (latitude longitude) / lognlambda=(0.277 -2.56); run;
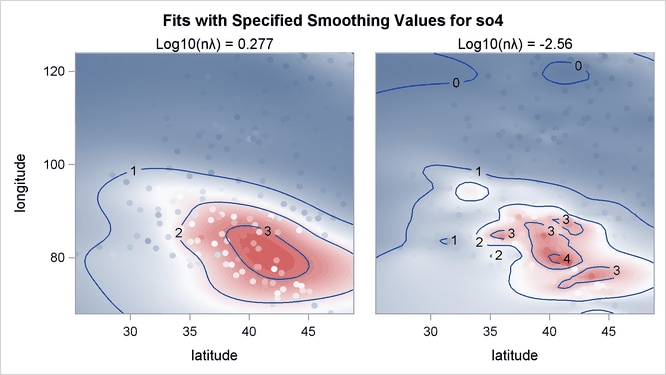
Output 96.3.5 shows the contour surfaces of two models with the two minima. The fit that corresponds to the global minimum 0.277 shows
a smoother fit that captures the general structure in the data set. The fit at the local minimum –2.56 is a rougher fit that
captures local details. The response values are also displayed as circles with the same color gradient by the default GRADIENT contour-option. The contrast between the predicted and observed SO![]() deposition is greater for the smoother fit than for the other one, which means the smoother fit has larger absolute residual
values.
deposition is greater for the smoother fit than for the other one, which means the smoother fit has larger absolute residual
values.
Output 96.3.5: Panel of Contour Fit Plots by 0.277 and –2.56
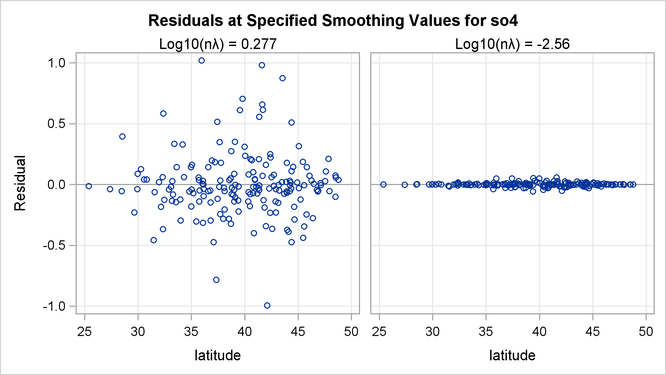
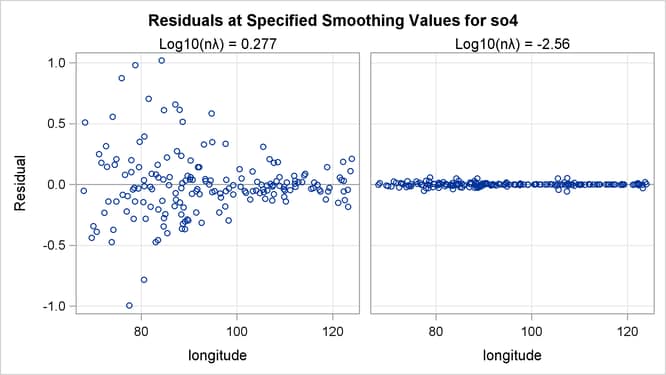
The residuals for the two fits can be visualized in RESIDUALBYSMOOTH panels. Output 96.3.6 is a panel of plots of residuals against smoothing variable Latitude. Output 96.3.7 is a panel of plots of residuals against smoothing variable Longitude. Both panels show that the residuals from the model with the global minimum are larger in absolute values than the ones from
the local minimum. This is expected, since the optimal model achieves the smallest GCV value by significantly increasing the
smoothness of fit and sacrificing a little in the goodness of fit.
Output 96.3.6: Panel of Residuals by Latitude Plots
Output 96.3.7: Panel of Residuals by Longitude Plots
In summary, the fit with ![]() represents the underlying surface, while the fit with the
represents the underlying surface, while the fit with the ![]() overfits the data and captures the additional noise component.
overfits the data and captures the additional noise component.
