The TPSPLINE Procedure

Andrews, D. W. K. (1988), Asymptotic Optimality of Generalized 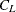, Cross-Validation, and Generalized Cross-Validation in Regression with Heteroskedastic Errors, Cowles Foundation Discussion Paper 906, Cowles Foundation for Research in Economics at Yale University, New Haven, CT, revised May 1989.

Bates, D., Lindstrom, M., Wahba, G., and Yandell, B. (1987), “GCVPACK-Routines for Generalized Cross Validation,” Communications in Statistics: Simulation and Computation, 16, 263–297.

Cleveland, W. S. (1993), Visualizing Data, Summit, NJ: Hobart Press.

Dongarra, J., Bunch, J., Moler, C., and Steward, G. (1979), Linpack Users’ Guide, Philadelphia: Society for Industrial and Applied Mathematics.

Duchon, J. (1976), “Fonctions-Spline et Espérances Conditionnelles de Champs Gaussiens,” Ann. Sci. Univ. Clermont Ferrand II Math., 14, 19–27.

Duchon, J. (1977), “Splines Minimizing Rotation-Invariant Semi-norms in Sobolev Spaces,” in W. Schempp and K. Zeller, eds., Constructive Theory of Functions of Several Variables, 85–100, New York: Springer-Verlag.

Hall, P. and Titterington, D. (1987), “Common Structure of Techniques for Choosing Smoothing Parameters in Regression Problems,” Journal of the Royal Statistical Society, Series B (Statistical Methodology), 49, 184–198.

Houghton, A. N., Flannery, J., and Viola, M. V. (1980), “Malignant Melanoma in Connecticut and Denmark,” International Journal of Cancer, 25, 95–104.

Hutchinson, M. and Bischof, R. (1983), “A New Method for Estimating the Spatial Distribution of Mean Seasonal and Annual Rainfall Applied to the Hunter Valley,” Australian Meteorological Magazine, 31, 179–184.

Meinguet, J. (1979), “Multivariate Interpolation at Arbitrary Points Made Simple,” Journal of Applied Mathematics and Physics (ZAMP), 30, 292–304.

Nychka, D. (1986a), The Average Posterior Variance of a Smoothing Spline and a Consistent Estimate of the Mean Square Error, Technical Report 168, North Carolina State University, Raleigh, NC.

Nychka, D. (1986b), A Frequency Interpretation of Bayesian ’Confidence’ Interval for Smoothing Splines, Technical Report 169, North Carolina State University, Raleigh.

Nychka, D. (1988), “Confidence Intervals for Smoothing Splines,” Journal of the American Statistical Association, 83, 1134–1143.

O’Sullivan, F. and Wong, T. (1987), Determining a Function Diffusion Coefficient in the Heat Equation, Technical report, Department of Statistics, University of California, Berkeley, CA.

Ramsay, J. and Silverman, B. (1997), Functional Data Analysis, New York: Springer-Verlag.

Seaman, R. and Hutchinson, M. (1985), “Comparative Real Data Tests of Some Objective Analysis Methods by Withholding,” Australian Meteorological Magazine, 33, 37–46.

Villalobos, M. and Wahba, G. (1987), “Inequality Constrained Multivariate Smoothing Splines with Application to the Estimation of Posterior Probabilities,” Journal of the American Statistical Association, 82, 239–248.

Wahba, G. (1983), “Bayesian ’Confidence Intervals’ for the Cross Validated Smoothing Spline,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 45, 133–150.

Wahba, G. (1990), Spline Models for Observational Data, Philadelphia: Society for Industrial and Applied Mathematics.

Wahba, G. and Wendelberger, J. (1980), “Some New Mathematical Methods for Variational Objective Analysis Using Splines and Cross Validation,” Monthly Weather Review, 108, 1122–1145.

Wang, Y. and Wahba, G. (1995), “Bootstrap Confidence Intervals for Smoothing Splines and Their Comparison to Bayesian Confidence Intervals,” Journal of Statistical Computation and Simulation, 51, 263–279.