The VARIOGRAM Procedure

COMPUTE Statement

COMPUTE computation-options ;

The COMPUTE statement provides a number of options that control the computation of the semivariance, the robust semivariance, and the covariance.

Table 102.2 summarizes the options available in the COMPUTE statement.

Table 102.2: COMPUTE Statement Options

Option	Description
ALPHA=	Specifies the confidence level
ANGLETOLERANCE=	Specifies the tolerance
AUTOCORRELATION	Calculates autocorrelation statistics
BANDWIDTH=	Specifies the bandwidth
CL	Requests confidence limits
DEPSILON=	Specifies the distance value for declaring that two distinct points are zero distance apart
LAGDISTANCE=	Specifies the basic distance unit that defines the lags
LAGTOLERANCE=	Specifies the tolerance around the LAGDISTANCE= value
MAXLAGS=	Specifies the maximum number of lag classes to be used
NDIRECTIONS=	Specifies the number of angle classes to be used
NHCLASSES=	Specifies the number of distance classes to be used
NOVARIOGRAM	Prevents the computation of the continuity measures
OUTPDISTANCE=	Specifies the cutoff distance for writing observations to the OUTPAIR= data set
ROBUST	Calculates a robust version of the semivarianc

ALPHA=number

specifies a parameter to obtain the confidence level for constructing confidence limits in the classical empirical semivariance estimation. The value of number must be in 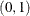, and the confidence level is 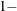number. The default is ALPHA=0.05, which corresponds to the default confidence level of 95%. If the CL option is not specified, ALPHA= is ignored.

ANGLETOLERANCE=angle-tolerance ANGLETOL=angle-tolerance ATOL=angle-tolerance

specifies the tolerance, in degrees, around the angles determined by the NDIRECTIONS= specification. The default is 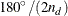$180^{\circ }/(2 n_ d)$ , where 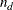${n_ d}$ is the NDIRECTIONS= specification. If you do not specify the NDIRECTIONS= option or the DIRECTIONS statement, ANGLETOLERANCE= is ignored.

See the section Theoretical and Computational Details of the Semivariogram for further information.

AUTOCORRELATION <(autocorrelation-options)> AUTOCORR <(autocorrelation-options)> AUTOC <(autocorrelation-options)>

specifies that autocorrelation statistics be calculated. You can further specify the following autocorrelation-options in parentheses following the AUTOCORRELATION option.

ASSUMPTION <= assumption-options> ASSUM <= assumption-options>

specifies the type of autocorrelation assumption to use. The assumption-options can be one of the following:

NORMALITY | NORMAL | NOR: specifies use of the normality assumption.
RANDOMIZATION | RANDOM | RAN: specifies use of the randomization assumption.

The default is ASSUMPTION=NORMALITY.

STATISTICS <= (stats-options)> STATS <= (stats-options)>

specifies the autocorrelation statistics in detail. The stats-options can be one or more of the following:

ALL: applies all available types of autoregression statistics.
GEARY | GEA: specifies use of the Geary’s c statistics.
MORAN | MOR: specifies use of the Moran’s I statistics.

The default is STATISTICS=ALL.

WEIGHTS <= weights-options> WEI <= weights-options>

specifies the scheme used for the computation of the autocorrelation weights. You can choose one of the following weights-options:

BINARY <(binary-option)>

specifies that binary weights be used. You also have the following binary-option:

ROWAVERAGING | ROWAVG | ROW: specifies that asymmetric autocorrelation weights be assigned to data pairs. For each observation, if there are nonzero weights, the ROWAVG option standardizes those weights so that they sum to 1. No row averaging is performed by default.

DISTANCE <(distance-options)>

specifies that autocorrelation weights be assigned based on the point pair distances. You also have the following distance-options:

NORMALIZE | NORMAL | NOR: specifies that normalized pair distances be used in the distance-based weights expression. The distances are normalized with respect to the maximum pairwise distance 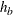, as it is defined in the section Computation of the Distribution Distance Classes. By default, nonnormalized values are used in the computations.
POWER=number POW=number: specifies the power to which the pair distance is raised in the distance-based weights expression. POWER is a nonnegative number, and its default value is POWER=1.
ROWAVERAGING | ROWAVG | ROW: specifies that asymmetric autocorrelation weights be assigned to data pairs. For each observation, if there are nonzero weights, the ROWAVG option standardizes those weights so that they sum to 1. No row averaging is performed by default.
SCALE=number SCA=number: specifies the scaling factor in the distance-based weights expression. SCALE is a nonnegative number, and its default value is SCALE=1.

The default is WEIGHTS=BINARY. See the section Autocorrelation Statistics for further details about the autocorrelation weights.

When you specify the AUTOCORRELATION option with no autocorrelation-options, PROC VARIOGRAM computes by default both the Moran’s I and Geary’s c statistics with p-values computed under the normality assumption with binary weights.

If you specify more than one ASSUMPTION in the autocorrelation-options, all but the last specified ASSUMPTION are ignored. The same holds if you specify more than one POWER= or SCALE= parameter in the WEIGHT=DISTANCE distance-options.

If you specify the WEIGHT=BINARY option in the AUTOCORRELATION option and the NOVARIOGRAM option at the same time, then you must also specify the LAGDISTANCE= option in the COMPUTE statement. See the section Autocorrelation Weights for more information.

BANDWIDTH=bandwidth-distance BANDW=bandwidth-distance

specifies the bandwidth, or perpendicular distance cutoff for determining the angle class for a given pair of points. The distance classes define a series of cylindrically shaped areas, while the angle classes radially cut these cylindrically shaped areas. For a given angle class 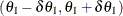$(\theta _1 - \delta \theta _1,\theta _1 + \delta \theta _1)$ , as you proceed out radially, the area encompassed by this angle class becomes larger. The BANDWIDTH= option restricts this area by excluding all points with a perpendicular distance from the line 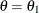$\theta = \theta _1$ that is greater than the BANDWIDTH= value. See Figure 102.23 for a visual representation of the bandwidth.

If you omit the BANDWIDTH= option, no restriction occurs. If you omit the NDIRECTIONS= option or the DIRECTIONS statement, BANDWIDTH= is ignored.

CL

requests confidence limits for the classical semivariance estimate. The lower bound of the confidence limits is always nonnegative, adhering to the behavior of the theoretical semivariance. You can control the confidence level with the ALPHA= option.

DEPSILON=distance-value DEPS=distance-value

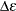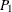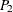specifies the distance value for declaring that two distinct points are zero distance apart. Such pairs, if they occur, cause numeric problems. If you specify DEPSILON= $\Delta \varepsilon$ , then pairs of points and for which the distance between them 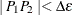$\mid P_1P_2 \mid < \Delta \varepsilon$ are excluded from the continuity measure calculations. The default value of the DEPSILON= option is 100 times the machine precision; this product is approximately 1E–10 on most computers.

LAGDISTANCE=distance-unit LAGDIST=distance-unit LAGD=distance-unit

specifies the basic distance unit that defines the lags. For example, a specification of LAGDISTANCE=x results in lag distance classes that are multiples of x. For a given pair of points 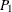and 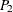, the distance between them, denoted 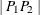$\mid P_1P_2 \mid$ , is calculated. If 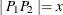$\mid P_1P_2 \mid = x$ , then this pair is in the first lag class. If 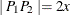$\mid P_1P_2 \mid = 2x$ , then this pair is in the second lag class, and so on.

For irregularly spaced data, the pairwise distances are unlikely to fall exactly on multiples of the LAGDISTANCE= value. In this case, a distance tolerance of 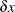$\delta x$ accommodates a spread of distances around multiples of x (the LAGTOLERANCE= option specifies the distance tolerance). For example, if 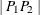$\mid P_1P_2 \mid$ is within 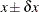$x \pm \delta x$ , you would place this pair in the first lag class; if 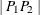$\mid P_1P_2 \mid$ is within 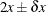$2x \pm \delta x$ , you would place this pair in the second lag class; and so on.

You can experiment and determine the candidate values for the LAGDISTANCE= option by plotting the pairwise distance histogram for different numbers of histogram classes, using the NHCLASSES= option.

A LAGDISTANCE= value is required for the semivariance and the autocorrelation computations. However, when you specify the NOVARIOGRAM option without the AUTOCORRELATION option, you need not specify the LAGDISTANCE= option.

See the section Theoretical and Computational Details of the Semivariogram for more information.

LAGTOLERANCE=tolerance-number LAGTOL=tolerance-number LAGT=tolerance-number

specifies the tolerance around the LAGDISTANCE= value for grouping distance pairs into lag classes. See the description of the LAGDISTANCE= option for information about the use of the LAGTOLERANCE= option, and the section Theoretical and Computational Details of the Semivariogram for more details.

If you omit the LAGTOLERANCE= option, a default value of 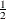$\frac{1}{2}$ times the LAGDISTANCE= value is used.

MAXLAGS=number-of-lags MAXLAG=number-of-lags MAXL=number-of-lags

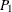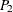specifies the maximum number of lag classes to be used in constructing the continuity measures in addition to a zero lag class; see also the section Distance Classification. This option excludes any pair of points and for which the distance between them, 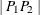$\mid P_1P_2 \mid$ , exceeds the MAXLAGS= value times the LAGDISTANCE= value.

You can determine candidate values for the MAXLAGS= option by plotting or displaying the OUTDISTANCE= data set.

A MAXLAGS= value is required unless you specify the NOVARIOGRAM option.

NDIRECTIONS=number-of-directions NDIR=number-of-directions ND=number-of-directions

specifies the number of angle classes to use in computing the continuity measures. This option is useful when there is potential anisotropy in the spatial continuity measures. Anisotropy is a field property in which the characterization of spatial continuity depends on the data pair orientation (or angle between the N–S direction and the axis defined by the data pair). Isotropy is the absence of this effect; that is, the description of spatial continuity depends only on the distance between the points, not the angle.

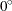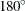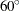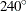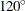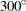The angle classes formed from the NDIRECTIONS= option start from N–S and proceed clockwise. For example, NDIRECTIONS=3 produces three angle classes. In terms of compass points, these classes are centered at $0^{\circ }$ (or its reciprocal, $180^{\circ }$ ), $60^{\circ }$ (or its reciprocal, $240^{\circ }$ ), and $120^{\circ }$ (or its reciprocal, $300^{\circ }$ ). 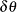For irregularly spaced data, the angles between pairs are unlikely to fall exactly in these directions, so an angle tolerance of $\delta \theta$ is used (the ANGLETOLERANCE= option specifies the angle tolerance). If NDIRECTIONS=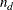, the base angle is 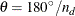$\theta =180^{\circ }/{n_ d}$ , and the angle classes are

$(k\theta - \delta \theta , k\theta + \delta \theta ) \hspace{0.5cm} k=0,\dots ,n_{d}-1$

If you omit the NDIRECTIONS= option, no angles are formed. This is the omnidirectional case where the spatial continuity measures are assumed to be isotropic.

The NDIRECTIONS= option is useful for exploring possible anisotropy. The DIRECTIONS statement, described in the section DIRECTIONS Statement, provides greater control over the angle classes.

See the section Theoretical and Computational Details of the Semivariogram for more information.

NHCLASSES=number-of-histogram-classes NHCLASS=number-of-histogram-classes NHC=number-of-histogram-classes

specifies the number of distance classes to consider in the spatial domain in the exploratory stage of the empirical semivariogram computation. The actual number of classes is one more than the NHCLASSES= value, since a special lag zero class is also computed. The NHCLASSES= option is used to produce the distance intervals table, the histogram of pairwise distances, and the OUTDISTANCE= data set. See the OUTDISTANCE= option, the section OUTDIST=SAS-data-set, and the section Theoretical and Computational Details of the Semivariogram for more information.

The default value is NHCLASSES=10.

NOVARIOGRAM

prevents the computation of the continuity measures. This option is useful for preliminary analysis, or when you require only the OUTDISTANCE= or OUTPAIR= data sets.

OUTPDISTANCE=distance-limit OUTPDIST=distance-limit OUTPD=distance-limit

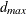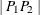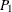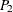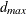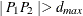specifies the cutoff distance for writing observations to the OUTPAIR= data set. If you specify OUTPDISTANCE= $d_{\mathit{max}}$ , the distance $\mid P_1P_2 \mid$ between each pair of points and is checked against $d_{\mathit{max}}$ . If $\mid P_1P_2 \mid > d_{\mathit{max}}$ , the observation for this pair is not written to the OUTPAIR= data set. If you omit the OUTPDISTANCE= option, all distinct pairs are written. This option is ignored if you omit the OUTPAIR= data set.

ROBUST

requests that a robust version of the semivariance be calculated in addition to the classical semivariance.