The LIFEREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesModel SpecificationComputational MethodSupported DistributionsPredicted ValuesConfidence IntervalsFit StatisticsProbability PlottingINEST= Data SetOUTEST= Data SetXDATA= Data SetComputational ResourcesBayesian AnalysisDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisODS Table NamesODS Graphics
Missing ValuesModel SpecificationComputational MethodSupported DistributionsPredicted ValuesConfidence IntervalsFit StatisticsProbability PlottingINEST= Data SetOUTEST= Data SetXDATA= Data SetComputational ResourcesBayesian AnalysisDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisODS Table NamesODS Graphics -
Examples
 Motorette FailureComputing Predicted Values for a Tobit ModelOvercoming Convergence Problems by Specifying Initial ValuesAnalysis of Arbitrarily Censored Data with Interaction EffectsProbability Plotting—Right CensoringProbability Plotting—Arbitrary CensoringBayesian Analysis of Clinical Trial DataModel Postfitting Analysis
Motorette FailureComputing Predicted Values for a Tobit ModelOvercoming Convergence Problems by Specifying Initial ValuesAnalysis of Arbitrarily Censored Data with Interaction EffectsProbability Plotting—Right CensoringProbability Plotting—Arbitrary CensoringBayesian Analysis of Clinical Trial DataModel Postfitting Analysis - References
The following statements create a SAS data set containing observed and right-censored lifetimes of 70 diesel engine fans (Nelson, 1982):
data Fan; input Lifetime Censor@@; Lifetime = Lifetime / 1000; datalines; 450 0 460 1 1150 0 1150 0 1560 1 1600 0 1660 1 1850 1 1850 1 1850 1 1850 1 1850 1 2030 1 2030 1 2030 1 2070 0 2070 0 2080 0 2200 1 3000 1 3000 1 3000 1 3000 1 3100 0 3200 1 3450 0 3750 1 3750 1 4150 1 4150 1 4150 1 4150 1 4300 1 4300 1 4300 1 4300 1 4600 0 4850 1 4850 1 4850 1 4850 1 5000 1 5000 1 5000 1 6100 1 6100 0 6100 1 6100 1 6300 1 6450 1 6450 1 6700 1 7450 1 7800 1 7800 1 8100 1 8100 1 8200 1 8500 1 8500 1 8500 1 8750 1 8750 0 8750 1 9400 1 9900 1 10100 1 10100 1 10100 1 11500 1 ;
Some of the fans had not failed at the time the data were collected, and the unfailed units have right-censored lifetimes. The variable LIFETIME represents either a failure time or a censoring time, in thousands of hours. The variable CENSOR is equal to 0 if the value of LIFETIME is a failure time, and it is equal to 1 if the value is a censoring time. The following statements use the LIFEREG procedure to produce the probability plot with an inset for the engine lifetimes:
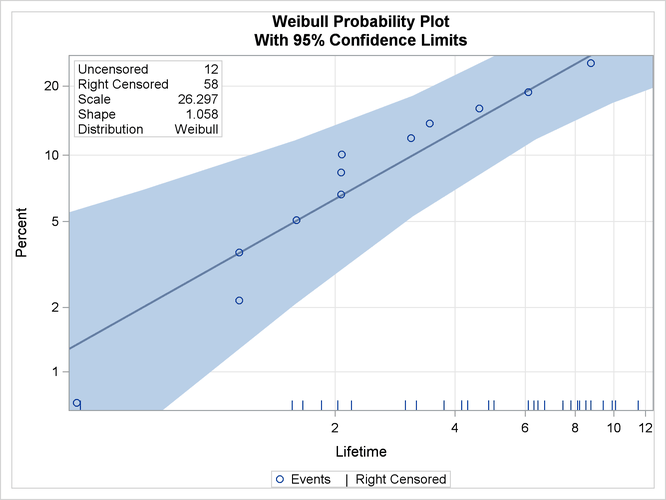
ods graphics on; proc lifereg data=Fan; model Lifetime*Censor( 1 ) = / d = Weibull; probplot ppout npintervals=simul; inset; run; ods graphics off;
The resulting graphical output is shown in Output 55.5.1. The estimated CDF, a line representing the maximum likelihood fit, and pointwise parametric confidence bands are plotted in the body of Output 55.5.1. The values of right-censored observations are plotted along the bottom of the graph. The “Cumulative Probability Estimates” table is also created in Output 55.5.2.
Output 55.5.2: CDF Estimates
| Cumulative Probability Estimates | |||||
|---|---|---|---|---|---|
| Lifetime | Cumulative Probability |
Simultaneous 95% Confidence Limits |
Kaplan-Meier Estimate |
Kaplan-Meier Standard Error |
|
| Lower | Upper | ||||
| 0.45 | 0.0071 | 0.0007 | 0.2114 | 0.0143 | 0.0142 |
| 1.15 | 0.0215 | 0.0033 | 0.2114 | 0.0288 | 0.0201 |
| 1.15 | 0.0360 | 0.0073 | 0.2168 | 0.0433 | 0.0244 |
| 1.6 | 0.0506 | 0.0125 | 0.2304 | 0.0580 | 0.0282 |
| 2.07 | 0.0666 | 0.0190 | 0.2539 | 0.0751 | 0.0324 |
| 2.07 | 0.0837 | 0.0264 | 0.2760 | 0.0923 | 0.0361 |
| 2.08 | 0.1008 | 0.0344 | 0.2972 | 0.1094 | 0.0392 |
| 3.1 | 0.1189 | 0.0436 | 0.3223 | 0.1283 | 0.0427 |
| 3.45 | 0.1380 | 0.0535 | 0.3471 | 0.1477 | 0.0460 |
| 4.6 | 0.1602 | 0.0653 | 0.3844 | 0.1728 | 0.0510 |
| 6.1 | 0.1887 | 0.0791 | 0.4349 | 0.2046 | 0.0581 |
| 8.75 | 0.2488 | 0.0884 | 0.6391 | 0.2930 | 0.0980 |