The LIFEREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesModel SpecificationComputational MethodSupported DistributionsPredicted ValuesConfidence IntervalsFit StatisticsProbability PlottingINEST= Data SetOUTEST= Data SetXDATA= Data SetComputational ResourcesBayesian AnalysisDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisODS Table NamesODS Graphics
Missing ValuesModel SpecificationComputational MethodSupported DistributionsPredicted ValuesConfidence IntervalsFit StatisticsProbability PlottingINEST= Data SetOUTEST= Data SetXDATA= Data SetComputational ResourcesBayesian AnalysisDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisODS Table NamesODS Graphics -
Examples
 Motorette FailureComputing Predicted Values for a Tobit ModelOvercoming Convergence Problems by Specifying Initial ValuesAnalysis of Arbitrarily Censored Data with Interaction EffectsProbability Plotting—Right CensoringProbability Plotting—Arbitrary CensoringBayesian Analysis of Clinical Trial DataModel Postfitting Analysis
Motorette FailureComputing Predicted Values for a Tobit ModelOvercoming Convergence Problems by Specifying Initial ValuesAnalysis of Arbitrarily Censored Data with Interaction EffectsProbability Plotting—Right CensoringProbability Plotting—Arbitrary CensoringBayesian Analysis of Clinical Trial DataModel Postfitting Analysis - References
Consider the data on melanoma patients from a clinical trial described in Ibrahim, Chen, and Sinha (2001). A partial listing of the data is shown in Output 55.7.1.
The survival time is modeled by a Weibull regression model with three covariates. An analysis of the right-censored survival data is performed with PROC LIFEREG to obtain Bayesian estimates of the regression coefficients by using the following SAS statements:
ods graphics on; proc lifereg data=e1684; class Sex; model Survtime*Survcens(1)=Age Sex Perform / dist=Weibull; bayes WeibullShapePrior=gamma seed=9999; run; ods graphics off;
Output 55.7.1: Clinical Trial Data
| Obs | survtime | survcens | age | sex | perform |
|---|---|---|---|---|---|
| 1 | 1.57808 | 2 | 35.9945 | 1 | 0 |
| 2 | 1.48219 | 2 | 41.9014 | 1 | 0 |
| 3 | 7.33425 | 1 | 70.2164 | 2 | 0 |
| 4 | 0.65479 | 2 | 58.1753 | 2 | 1 |
| 5 | 2.23288 | 2 | 33.7096 | 1 | 0 |
| 6 | 9.38356 | 1 | 47.9726 | 1 | 0 |
| 7 | 3.27671 | 2 | 31.8219 | 2 | 0 |
| 8 | 0.00000 | 1 | 72.3644 | 2 | 0 |
| 9 | 0.80274 | 2 | 40.7151 | 2 | 0 |
| 10 | 9.64384 | 1 | 32.9479 | 1 | 0 |
| 11 | 1.66575 | 2 | 35.9205 | 1 | 0 |
| 12 | 0.94247 | 2 | 40.5068 | 2 | 0 |
| 13 | 1.68767 | 2 | 57.0384 | 1 | 0 |
| 14 | 5.94247 | 2 | 63.1452 | 1 | 0 |
| 15 | 2.34247 | 2 | 62.0630 | 1 | 0 |
| 16 | 0.89863 | 2 | 56.5342 | 1 | 1 |
| 17 | 9.03288 | 1 | 22.9945 | 2 | 0 |
| 18 | 9.63014 | 1 | 18.4712 | 1 | 0 |
| 19 | 0.52603 | 2 | 41.2521 | 1 | 0 |
| 20 | 1.82192 | 2 | 29.5178 | 1 | 0 |
Maximum likelihood estimates of the model parameters shown in Output 55.7.2 are displayed by default.
Output 55.7.2: Maximum Likelihood Parameter Estimates
| Analysis of Maximum Likelihood Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | ||
| Intercept | 1 | 2.4402 | 0.3716 | 1.7119 | 3.1685 | |
| age | 1 | -0.0115 | 0.0070 | -0.0253 | 0.0023 | |
| sex | 1 | 1 | -0.1170 | 0.1978 | -0.5046 | 0.2707 |
| sex | 2 | 0 | 0.0000 | . | . | . |
| perform | 1 | 0.2905 | 0.3222 | -0.3411 | 0.9220 | |
| Scale | 1 | 1.2537 | 0.0824 | 1.1021 | 1.4260 | |
| Weibull Shape | 1 | 0.7977 | 0.0524 | 0.7012 | 0.9073 | |
Since no prior distributions for the regression coefficients were specified, the default uniform improper distributions shown in the “Uniform Prior for Regression Coefficients” table in Output 55.7.3 are used. The specified gamma prior for the Weibull shape parameter is also shown in Output 55.7.3.
Output 55.7.3: Model Parameter Priors
| Uniform Prior for Regression Coefficients |
|
|---|---|
| Parameter | Prior |
| Intercept | Constant |
| age | Constant |
| sex1 | Constant |
| perform | Constant |
| Independent Prior Distributions for Model Parameters | |||||
|---|---|---|---|---|---|
| Parameter | Prior Distribution | Hyperparameters | |||
| Weibull Shape | Gamma | Shape | 0.001 | Inverse Scale | 0.001 |
Fit statistics, descriptive statistics, interval statistics, and the sample parameter correlation matrix for the posterior sample are displayed in the tables in Output 55.7.4. Since noninformative prior distributions for the regression coefficients were used, the mean and standard deviations of the posterior distributions for the model parameters are close to the maximum likelihood estimates and standard errors.
Output 55.7.4: Posterior Sample Statistics
| Fit Statistics | |
|---|---|
| DIC (smaller is better) | 875.251 |
| pD (effective number of parameters) | 4.984 |
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| Intercept | 10000 | 2.4668 | 0.3862 | 2.1989 | 2.4621 | 2.7256 |
| age | 10000 | -0.0115 | 0.00733 | -0.0163 | -0.0115 | -0.00652 |
| sex1 | 10000 | -0.1255 | 0.2004 | -0.2584 | -0.1247 | 0.00817 |
| perform | 10000 | 0.3304 | 0.3317 | 0.1071 | 0.3188 | 0.5470 |
| WeibShape | 10000 | 0.7834 | 0.0518 | 0.7481 | 0.7815 | 0.8178 |
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| Intercept | 0.050 | 1.7279 | 3.2368 | 1.7234 | 3.2264 |
| age | 0.050 | -0.0260 | 0.00263 | -0.0261 | 0.00244 |
| sex1 | 0.050 | -0.5197 | 0.2676 | -0.5260 | 0.2583 |
| perform | 0.050 | -0.2898 | 1.0072 | -0.3200 | 0.9726 |
| WeibShape | 0.050 | 0.6846 | 0.8905 | 0.6805 | 0.8849 |
| Posterior Correlation Matrix | |||||
|---|---|---|---|---|---|
| Parameter | Intercept | age | sex1 | perform | WeibShape |
| Intercept | 1.0000 | -.9018 | -.3099 | -.0888 | -.1140 |
| age | -.9018 | 1.0000 | -.0259 | -.0363 | 0.0493 |
| sex1 | -.3099 | -.0259 | 1.0000 | 0.1248 | 0.0371 |
| perform | -.0888 | -.0363 | 0.1248 | 1.0000 | -.0355 |
| WeibShape | -.1140 | 0.0493 | 0.0371 | -.0355 | 1.0000 |
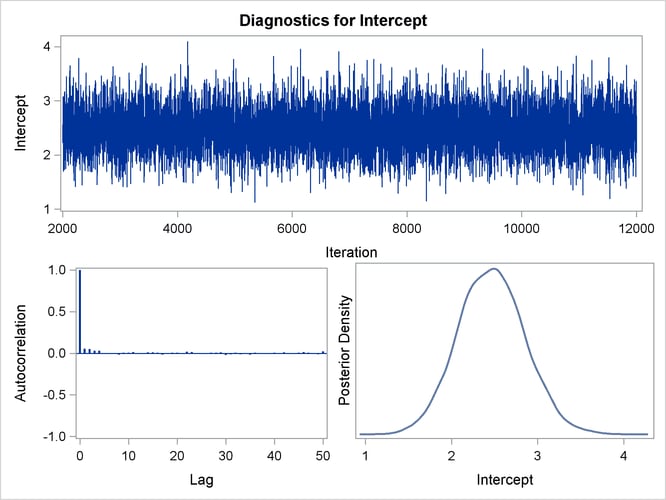
The default diagnostic statistics are displayed in Output 55.7.5. See the section Assessing Markov Chain Convergence in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details on Bayesian convergence diagnostics.
Output 55.7.5: Convergence Diagnostics
| Posterior Autocorrelations | ||||
|---|---|---|---|---|
| Parameter | Lag 1 | Lag 5 | Lag 10 | Lag 50 |
| Intercept | 0.0564 | 0.0030 | 0.0082 | 0.0234 |
| age | -0.0079 | -0.0184 | -0.0015 | 0.0239 |
| sex1 | 0.6293 | 0.0700 | 0.0055 | -0.0199 |
| perform | 0.6514 | 0.0773 | 0.0397 | -0.0123 |
| WeibShape | 0.0719 | -0.0083 | -0.0062 | 0.0112 |
| Geweke Diagnostics | ||
|---|---|---|
| Parameter | z | Pr > |z| |
| Intercept | 0.4962 | 0.6198 |
| age | -0.4119 | 0.6804 |
| sex1 | -0.2519 | 0.8011 |
| perform | -0.1049 | 0.9165 |
| WeibShape | -0.6573 | 0.5110 |
| Effective Sample Sizes | |||
|---|---|---|---|
| Parameter | ESS | Autocorrelation Time |
Efficiency |
| Intercept | 7476.1 | 1.3376 | 0.7476 |
| age | 10000.0 | 1.0000 | 1.0000 |
| sex1 | 2482.1 | 4.0288 | 0.2482 |
| perform | 2174.0 | 4.5998 | 0.2174 |
| WeibShape | 8538.8 | 1.1711 | 0.8539 |
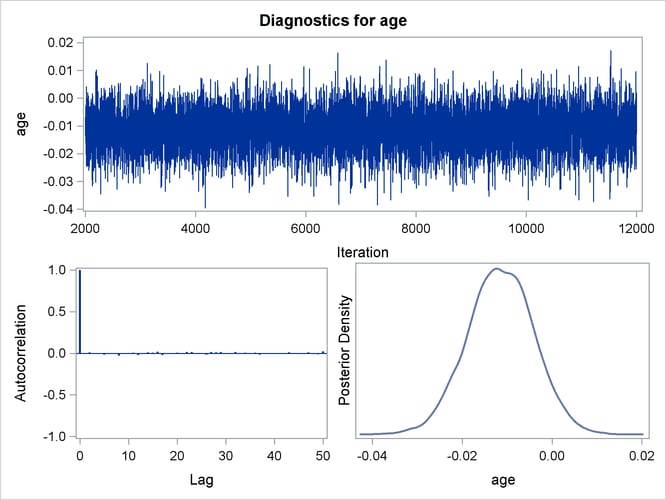
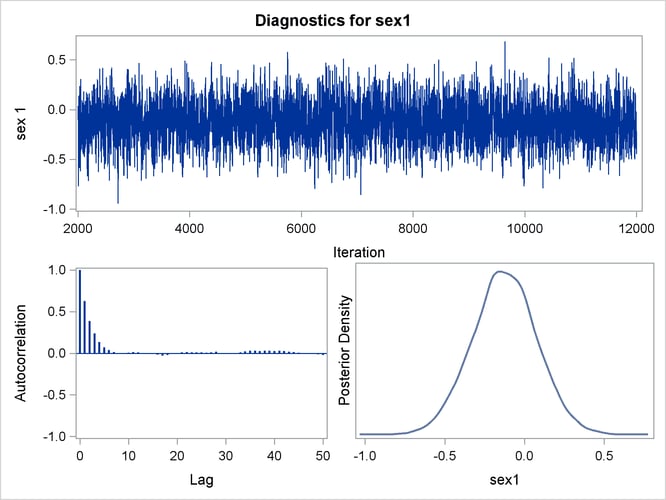
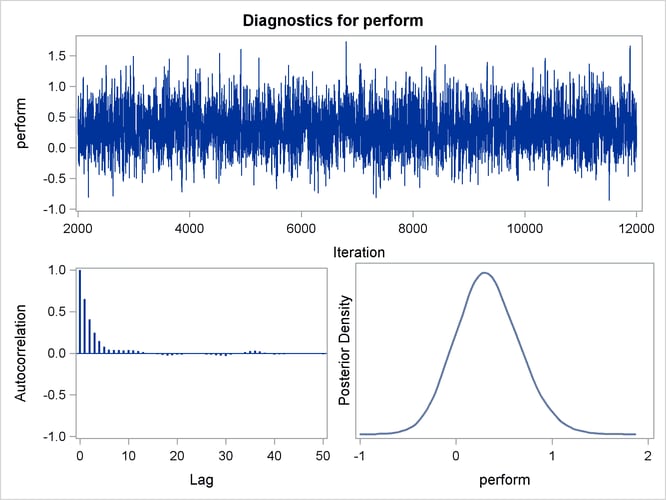
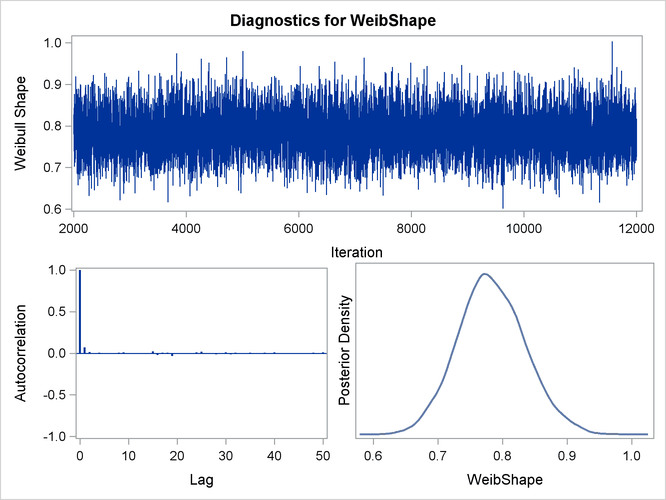
Trace, autocorrelation, and density plots for the seven model parameters are shown in Output 55.7.6 through Output 55.7.10. These plots show no indication that the Markov chains have not converged. See the sections Assessing Markov Chain Convergence and Visual Analysis via Trace Plots in Chapter 7: Introduction to Bayesian Analysis Procedures, for more information about assessing the convergence of the chain of posterior samples.