-
ALPHA=
 <( <LOWER=
<( <LOWER=
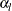 > <UPPER=
> <UPPER=
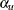 > )>
> )>
-
specifies the Type I error probability  .
The default is
.
The default is 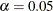 . The LOWER= and UPPER= options are applicable only for the two-sided design. The LOWER= option specifies the lower Type I
error probability
. The LOWER= and UPPER= options are applicable only for the two-sided design. The LOWER= option specifies the lower Type I
error probability 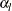 , and the upper Type I error probability is computed as
, and the upper Type I error probability is computed as 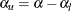 . The UPPER= option specifies the upper Type I error probability
. The UPPER= option specifies the upper Type I error probability 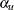 , and the lower Type I error probability is computed as
, and the lower Type I error probability is computed as 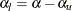 . If both LOWER= and UPPER= options are not specified,
. If both LOWER= and UPPER= options are not specified, 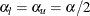 .
.
If both the MAXINFO= and ALTREF= options are specified, then the Type I and Type II error probability levels cannot be met
simultaneously. In this case, the ALPHA= option is applicable only with the BOUNDARYKEY=ALPHA option (which is the default),
and the Type II error probability 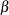 is derived.
is derived.
-
ALT=LOWER | UPPER | TWOSIDED
-
specifies the type of alternative hypothesis in the design.
For a test of 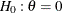 , the keywords LOWER, UPPER, and TWOSIDED correspond to the alternatives of
, the keywords LOWER, UPPER, and TWOSIDED correspond to the alternatives of 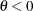 ,
, 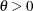 , and
, and 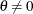 , respectively. The default is ALT=TWOSIDED.
, respectively. The default is ALT=TWOSIDED.
-
BETA=
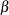 <( <LOWER=
<( <LOWER=
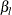 > <UPPER=
> <UPPER=
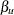 > )>
> )>
-
specifies the Type II error probability level 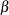 .
The default is
.
The default is 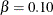 . The LOWER= and UPPER= options are applicable only for the two-sided design. The LOWER= option specifies the lower Type II
error probability level
. The LOWER= and UPPER= options are applicable only for the two-sided design. The LOWER= option specifies the lower Type II
error probability level 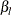 , and the UPPER= option specifies the upper Type II error probability level
, and the UPPER= option specifies the upper Type II error probability level 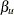 . If the LOWER= or UPPER= option is not specified,
. If the LOWER= or UPPER= option is not specified, 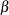 is used.
is used.
If both the MAXINFO= and ALTREF= options are specified, then the Type I and Type II error probability levels cannot be met
simultaneously. In this case, the BETA= option is applicable only with the BOUNDARYKEY=BETA option, and the Type I error probability
 is derived.
is derived.
-
BETAOVERLAP=ADJUST | NOADJUST
OVERLAP=ADJUST | NOADJUST
-
specifies whether to check for overlapping of the lower and upper
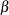 boundaries for the two corresponding one-sided tests. This option applies to two-sided designs with STOP=ACCEPT or STOP=BOTH
that are constructed with error spending methods, and this type of overlapping might result from a small
boundaries for the two corresponding one-sided tests. This option applies to two-sided designs with STOP=ACCEPT or STOP=BOTH
that are constructed with error spending methods, and this type of overlapping might result from a small 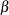 spending at an interim stage. When you specify BETAOVERLAP=ADJUST, the procedure checks for this type of overlapping. If
such overlapping is found, the
spending at an interim stage. When you specify BETAOVERLAP=ADJUST, the procedure checks for this type of overlapping. If
such overlapping is found, the 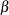 boundaries for the two-sided design at that stage are set to missing, and the
boundaries for the two-sided design at that stage are set to missing, and the 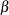 spending values at subsequent stages are adjusted, as described in the section Boundary Adjustments for Overlapping Lower and Upper
spending values at subsequent stages are adjusted, as described in the section Boundary Adjustments for Overlapping Lower and Upper 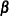 Boundaries".
Boundaries".
You can specify BETAOVERLAP=NOADJUST to request that no adjustment be made. The default is BETAOVERLAP=ADJUST.
-
BOUNDARYKEY=ALPHA | BETA | BOTH | NONE
-
specifies types of errors to be maintained in the resulting boundary.
The default is BOUNDARYKEY=ALPHA if both ALTREF= and MAXINFO= options are specified. Otherwise, the default is BOUNDARYKEY=NONE
for Whitehead methods with the STOP=BOTH option, and it is BOUNDARYKEY=BOTH for others.
See the section Applicable Boundary Keys for a detailed description of applicable boundary keys.
-
INFO=EQUAL | CUM( numbers )
-
specifies relative information levels for all stages in the design.
The INFO=EQUAL option specifies equally spaced information levels, and the INFO=CUM option specifies cumulative relative information
levels. The default is INFO=EQUAL.
If the number of information levels specified in the INFO=CUM option is less than the number of stages specified in the NSTAGES=
option, the last available information increment is used as the information increment for each subsequent stage.
-
METHOD=WHITEHEAD < ( TAU=
 < ( <LOWER=
< ( <LOWER=
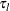 > <UPPER=
> <UPPER=
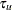 > ) > ) >
> ) > ) >
METHOD=method
METHOD(boundary) = method
-
specifies the methods for the boundaries in the design,
where 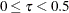 .
.
For a one-sided design, an  boundary is created with the STOP=REJECT or STOP=BOTH option, and a
boundary is created with the STOP=REJECT or STOP=BOTH option, and a 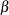 boundary is created with the STOP=ACCEPT or STOP=BOTH option. For a two-sided design, lower and upper
boundary is created with the STOP=ACCEPT or STOP=BOTH option. For a two-sided design, lower and upper  boundaries are created with the STOP=REJECT or STOP=BOTH option, and lower and upper
boundaries are created with the STOP=REJECT or STOP=BOTH option, and lower and upper 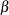 boundaries are created with the STOP=ACCEPT or STOP=BOTH option.
boundaries are created with the STOP=ACCEPT or STOP=BOTH option.
There are three types of methods available in the SEQDESIGN procedure. The unified family methods and Haybittle-Peto methods
derive boundary values with fixed boundary shape; the Whitehead methods derive boundary values by adjusting the boundary values
generated from continuous monitoring; and the error spending methods derive the boundary values from the specified errors
used at each stage. You can specify different methods for the same design, but all methods must be from the same group.
For a design with early stopping to reject or accept the null hypothesis, the METHOD=WHITEHEAD option uses Whitehead’s triangular
design
and double-triangular design
for a one-sided design and two-sided design, respectively (Whitehead and Stratton, 1983; Whitehead, 1997, 2001). For a design with early stopping only to reject the null hypothesis or only to accept the null hypothesis, you can specify
the slope of the boundary line in the score statistic scale with the TAU=  option. The default is TAU=0.25. See the section Whitehead Methods for a detailed description of the Whitehead methods.
option. The default is TAU=0.25. See the section Whitehead Methods for a detailed description of the Whitehead methods.
The following options specify available error spending methods for the boundary. Each of these methods can be specified with the METHOD= option
for all boundaries, or with the METHOD(boundary) = option for an individual boundary. See the section Error Spending Methods for a detailed description of these error spending methods.
-
ERRFUNCGAMMA < ( GAMMA=
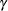 ) >
) >
-
specifies a gamma cumulative error spending function for the boundary
(Hwang, Shih, and DeCani, 1990). The GAMMA= option specifies the gamma parameter 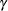 in the function, where
in the function, where 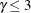 . The boundaries created with
. The boundaries created with 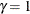 are similar to the boundaries from the Pocock method, and the boundaries created with
are similar to the boundaries from the Pocock method, and the boundaries created with 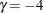 or
or 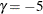 are similar to the boundaries from the O’Brien-Fleming method. The default is GAMMA=–2, which is the average of
are similar to the boundaries from the O’Brien-Fleming method. The default is GAMMA=–2, which is the average of 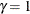 and
and 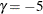 .
.
-
ERRFUNCOBF
-
specifies the O’Brien-Fleming-type cumulative error spending function
for the boundary (Lan and DeMets, 1983).
-
ERRFUNCPOC
-
specifies the Pocock-type cumulative error spending function
for the boundary (Lan and DeMets, 1983).
-
ERRFUNCPOW < ( RHO=
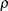 ) >
) >
-
specifies a power cumulative error spending function for the boundary
(Jennison and Turnbull, 2000, p. 148). The RHO= option specifies the power parameter 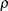 in the function, where
in the function, where 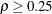 . The boundaries created with
. The boundaries created with 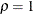 are similar to the boundaries from the Pocock method, and the boundaries created with
are similar to the boundaries from the Pocock method, and the boundaries created with 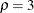 are similar to the boundaries from the O’Brien-Fleming method. The default is RHO=2, which is the average of
are similar to the boundaries from the O’Brien-Fleming method. The default is RHO=2, which is the average of 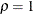 and
and 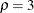 .
.
-
ERRSPEND ( numbers )
-
specifies the relative cumulative error spending at each stage.
With a fixed boundary shape, you can use the following available Haybittle-Peto methods and unified family methods to derive
the boundary. You can specify each of these methods in the METHOD= option for all boundaries, or in the METHOD(boundary) = option for an individual boundary. See the section Haybittle-Peto Method for a detailed description of the Haybittle-Peto methods, and see the section Unified Family Methods for a detailed description of unified family methods.
-
HP | HAYBITTLE | PETO < ( Z= numbers | PVALUE= numbers ) >
-
specifies the Haybittle-Peto method
(Haybittle, 1971; Peto et al., 1976). The values specified are used to create the boundary values. The boundary value at the final stage can be derived in the
procedure to maintain the Type I and Type II error probability levels. The default is Z=3.
-
OBF | OBRIENFLEMING
-
specifies the O’Brien-Fleming method
(O’Brien and Fleming, 1979). The O’Brien-Fleming method is equivalent to a power family method with RHO=0.5.
-
POC | POCOCK
-
specifies the Pocock method
(Pocock, 1977). The Pocock method is equivalent to a power family method with RHO=0.
-
POW | POWER < ( RHO=
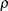 ) >
) >
-
specifies a power family method
(Wang and Tsiatis, 1987; Emerson and Fleming, 1989; Pampallona and Tsiatis, 1994). The RHO= option specifies the power parameter 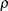 in the power family method, where
in the power family method, where 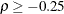 . The power family method with
. The power family method with 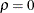 corresponds to the Pocock method, and the power family method with
corresponds to the Pocock method, and the power family method with 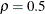 corresponds to the O’Brien-Fleming method. The default is RHO=0.25, a value halfway between the Pocock and O’Brien-Fleming
methods. A power family method is equivalent to a unified family method with RHO=
corresponds to the O’Brien-Fleming method. The default is RHO=0.25, a value halfway between the Pocock and O’Brien-Fleming
methods. A power family method is equivalent to a unified family method with RHO=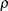 and TAU=0.
and TAU=0.
-
TRI | TRIANGULAR < ( TAU=
 ) >
) >
-
specifies a unified family triangular method
(Kittelson and Emerson, 1999), where 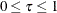 . The default is TAU=1.0. The triangular method is identical to the unified family method with RHO=0.5 and TAU=
. The default is TAU=1.0. The triangular method is identical to the unified family method with RHO=0.5 and TAU= . Note that this unified family triangular method is different from Whitehead’s triangular method.
. Note that this unified family triangular method is different from Whitehead’s triangular method.
-
UNI | UNIFIED < ( <TAU=
 > <RHO=
> <RHO=
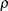 > ) >
> ) >
-
specifies a unified family method
(Kittelson and Emerson, 1999). The TAU= and RHO= options specify the  and
and 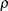 parameters in a unified family method, respectively, where
parameters in a unified family method, respectively, where 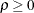 and
and 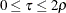 . The defaults are TAU=0 and RHO=0.25. See the section Unified Family Methods for a detailed description of the unified family methods.
. The defaults are TAU=0 and RHO=0.25. See the section Unified Family Methods for a detailed description of the unified family methods.
The O’Brien-Fleming, Pocock, power family, and triangular methods are all special cases of the unified family methods. Table 87.3 summarizes the corresponding parameters in the unified family for these methods.
Table 87.3: Parameters in the Unified Family for Various Methods
| |
|
|
Unified Family
|
|
Method
|
Option
|
|
Rho
|
Tau
|
|
Pocock
|
POC
|
|
0
|
0
|
|
O’Brien-Fleming
|
OBF
|
|
0.5
|
0
|
|
Power family
|
POW (RHO=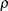 ) )
|
|
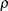
|
0
|
|
Triangular
|
TRI (TAU= ) )
|
|
0.5
|

|
Note that the power parameter 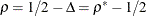 , where
, where 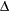 is the power parameter used in Jennison and Turnbull (2000) and Wang and Tsiatis (1987) and
is the power parameter used in Jennison and Turnbull (2000) and Wang and Tsiatis (1987) and 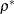 is the power parameter used in Kittelson and Emerson (1999).
is the power parameter used in Kittelson and Emerson (1999).
If a method with specified parameters is used for all boundaries in the design, you can use the METHOD= option to specify
the method. Otherwise, you can use the following METHOD(boundary)= options to specify different methods from the same group for the boundaries.
-
METHOD(ALPHA)=method
METHOD(REJECT)=method
-
specifies the method for the  boundary of a one-sided design or the lower and upper
boundary of a one-sided design or the lower and upper  boundaries for a two-sided design.
boundaries for a two-sided design.
-
METHOD(LOWERALPHA)=method
METHOD(LOWERREJECT)=method
-
specifies the method for the lower  boundary of a two-sided design.
boundary of a two-sided design.
-
METHOD(UPPERALPHA)=method
METHOD(UPPERREJECT)=method
-
specifies the method for the upper  boundary of a two-sided design.
boundary of a two-sided design.
-
METHOD(BETA)=method
METHOD(ACCEPT)=method
-
specifies the method for the 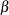 boundary of a one-sided design or the lower and upper
boundary of a one-sided design or the lower and upper 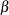 boundaries for a two-sided design.
boundaries for a two-sided design.
-
METHOD(LOWERBETA)=method
METHOD(LOWERACCEPT)=method
-
specifies the method for the lower 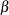 boundary of a two-sided design.
boundary of a two-sided design.
-
METHOD(UPPERBETA)=method
METHOD(UPPERACCEPT)=method
-
specifies the method for the upper 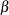 boundary of a two-sided design.
boundary of a two-sided design.
-
NSTAGES=number
-
specifies the number of stages for the design. This option is required in the DESIGN statement, and the maximum allowed number
of stages is 25.
-
STOP=ACCEPT
STOP=REJECT
STOP=BOTH < ( BETABOUNDARY=BINDING | NONBINDING ) >
-
specifies the early stopping criterion for the design. The keywords ACCEPT, REJECT, and BOTH correspond to early stopping
only to accept, only to reject, and either to accept or reject the null hypothesis 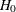 , respectively. The default is STOP=REJECT. With STOP=BOTH, the BETABOUNDARY=BINDING suboption computes the Type I error probability
with the acceptance boundary, and the BETABOUNDARY=NONBINDING suboption computes the Type I error probability without the
acceptance boundary.
The default is BETABOUNDARY=BINDING. The BETABOUNDARY=NONBINDING option is not applicable with METHOD=WHITEHEAD.
, respectively. The default is STOP=REJECT. With STOP=BOTH, the BETABOUNDARY=BINDING suboption computes the Type I error probability
with the acceptance boundary, and the BETABOUNDARY=NONBINDING suboption computes the Type I error probability without the
acceptance boundary.
The default is BETABOUNDARY=BINDING. The BETABOUNDARY=NONBINDING option is not applicable with METHOD=WHITEHEAD.


 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual