The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 Tests and Joint TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsCaution about Using Survival Data with Left TruncationEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics
Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 Tests and Joint TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsCaution about Using Survival Data with Left TruncationEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data
Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data - References
The product-limit estimator is used in a number of instances in the PHREG procedure, such as to transform the time values in the ZPH option in the PROC PHREG statement. The product-limit estimator is also used to construct the weights in the inverse probability of censoring weighting (IPCW) techniques, which are adapted to fit the proportional subdistribution model of Fine and Gray (1999) for competing-risks data and to assess the predictive accuracy of a model (Schemper and Henderson, 2000). Although the product-limit estimator is the gold standard for estimating the survivor function of right-censored data, it might not be meaningful for right-censored data with left-truncation, as illustrated by Example 4.3 in Klein and Moeschberger (2003). In their example, 94 men and 365 women passed through the Channing House Retirement Center between January 1964 and July 1975. The outcome is the time to death, using the natural metric of age (in months).
The following statements create the data set Channing, which contains the following variables:
-
Gender: female or male -
Age_entry: age at entry, in months -
Age_exit: age at exit (death or last follow-up), in months -
Death: death indicator, with the value 1 for death and 0 for censoring
data Channing; input Gender$ Age_entry Age_exit Death @@; datalines; Female 1042 1172 1 Female 921 1040 1 Female 885 1003 1 Female 901 1018 1 Female 808 932 1 Female 915 1004 1 Female 901 1023 1 Female 852 908 1 Female 828 868 1 Female 968 990 1 Female 936 1033 1 Female 977 1056 1 Female 929 999 1 Female 936 1064 1 Female 1016 1122 1 Female 910 1020 1 Female 1140 1200 1 Female 1015 1056 1 Female 850 940 1 Female 895 996 1 Female 854 969 1 ... more lines ... Male 751 777 1 Male 906 966 1 Male 835 907 1 Male 946 1031 1 Male 759 781 1 Male 909 914 0 Male 962 998 1 Male 984 1022 1 Male 891 932 1 Male 835 898 1 Male 1039 1060 1 Male 1010 1044 1 ;
The following statements use the PHREG procedure to save the product-limit estimate of the survivor function for each gender
in the data set Outs. For each gender, the number of subjects at risk and the number of deaths at each death time are captured in the data set
Atrisk. By merging these two data sets, Outs and Atrisk, you can conveniently display side by side the number of subjects at risk, the number of deaths, and the product-limit survival
estimate at each death time.
ods graphics on; proc phreg data=Channing plots(overlay=row)=survival atrisk; model Age_exit*Death(0)= /entrytime=Age_entry; strata Gender; baseline out=Outs survival=Probability / method=pl; ods output RiskSetInfo=Atrisk; run;
data Outs; set Outs; if Gender="Female" then StratumNumber=1; else StratumNumber=2; run; data Outs; merge atrisk outs; by StratumNumber Age_exit; run;
proc print data=Outs; id Gender; var Age_exit Atrisk Event Probability; run;
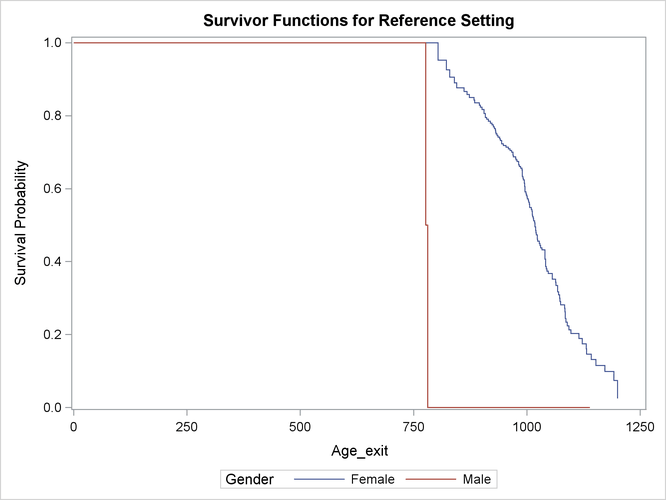
Figure 73.18 displays two product-limit survival curves, one for women and one for men. The survival probabilities are tabulated in Figure 73.19 for women and in Figure 73.20 for men. Although the survival curve for women does not appear unusual, the survival curve for men looks odd, because the
curve drops to 0 at 781 months even though the majority of men survive beyond 781 months. At 781 months, the risk set consists
of a single time to death, rendering the product-limit estimate as 0 at 781 months and thereafter. The product-limit curve
for men for these data is meaningless. Klein and Moeschberger (2003) suggest using only those observations in which the value of Age_exit exceeds 781 months.
Figure 73.19: Product-Limit Survival Probabilities for Women
| Gender | Age_exit | Atrisk | Event | Probability |
|---|---|---|---|---|
| Female | 0 | . | . | 1.00000 |
| Female | 804 | 21 | 1 | 0.95238 |
| Female | 822 | 36 | 1 | 0.92593 |
| Female | 830 | 46 | 1 | 0.90580 |
| Female | 840 | 58 | 1 | 0.89018 |
| Female | 845 | 66 | 1 | 0.87669 |
| Female | 861 | 89 | 1 | 0.86684 |
| . | . | . | . | |
| . | . | . | . | |
| . | . | . | . | |
| Female | 1152 | 8 | 1 | 0.11493 |
| Female | 1172 | 7 | 1 | 0.09852 |
| Female | 1192 | 4 | 1 | 0.07389 |
| Female | 1200 | 3 | 2 | 0.02463 |
PROC PHREG currently makes no attempt to circumvent the problem of the invalid product-limit estimator for left-truncated data.