The QUANTREG Procedure

The QUANTREG procedure assigns a name to each graph it creates. You can use these names to refer to the graphs when you use ODS. The names along with the required statements and options are listed in Table 83.11.

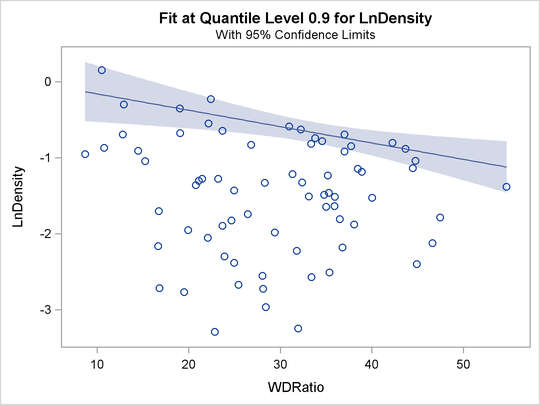
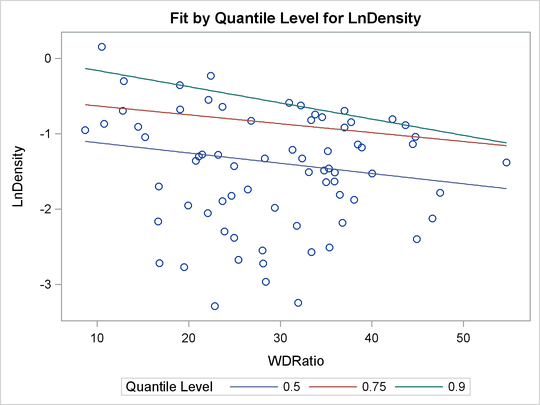
When the model has a single independent continuous variable (with or without the intercept), the QUANTREG procedure automatically creates a plot of fitted conditional quantiles against this independent variable for one or more quantiles that are specified in the MODEL statement.

The following example reuses the trout data set in the section Analysis of Fish-Habitat Relationships to show the fit plot for one or several quantiles:

ods graphics on;

proc quantreg data=trout ci=resampling;
   model LnDensity = WDRatio / quantile=0.9 seed=1268;
run;

proc quantreg data=trout ci=resampling;
   model LnDensity = WDRatio / quantile=0.5 0.75 0.9 seed=1268;
run;

For a single quantile, the confidence limits for the fitted conditional quantiles are also plotted if you specify the CI=RESAMPLING or CI=SPARSITY option. (See Figure 83.14.) For multiple quantiles, confidence limits are not plotted by default. (See Figure 83.15.) You can add the confidence limits on the plot by specifying the option PLOT=FITPLOT(SHOWLIMITS).

The QUANTREG procedure also provides fit plots for quantile regression splines and polynomials if they are based on a single continuous variable. (See Example 83.4 and Example 83.5 for some examples.)

Figure 83.14: Fit Plot with Confidence Limits

Figure 83.15: Fit Plot for Multiple Quantiles

A quantile process plot is a scatter plot of an estimated regression parameter against a quantile. You can request this plot by specifying the PLOT=QUANTPLOT option in the MODEL statement when multiple regression quantiles are computed or when the entire quantile process is computed. Quantile process plots are often used to check model variations at different quantiles, which is usually called model heterogeneity.

By default, panels are used to hold multiple process plots (up to four in each panel). You can use the UNPACK option to request individual process plots. Figure 83.10 in the section Analysis of Fish-Habitat Relationships shows a panel that includes two quantile process plots. Output 83.2.9 in Example 83.2 shows a single quantile process plot. Example 83.3 demonstrates more quantile process plots and their usage.

The distance-distance plot (DDPLOT) is mainly used for leverage-point diagnostics. It is a scatter plot of the robust distances against the classical Mahalanobis distances for the continuous independent variables. For more information about the robust distance, see the section Leverage Point and Outlier Detection. If is a classification variable is specified in the model, this plot is not created.

You can use the PLOT=DDPLOT option to request this plot. The following statements use the growth data set in Example 83.2 to create a single plot, which is shown in Output 83.2.4 in Example 83.2:

ods graphics on;

proc quantreg data=growth ci=resampling plot=ddplot;
   model GDP = lgdp2 mse2 fse2 fhe2 mhe2 lexp2
               lintr2 gedy2 Iy2 gcony2 lblakp2 pol2 ttrad2
               / quantile=.5 diagnostics leverage(cutoff=8) seed=1268;
   id Country;
run;

The reference lines represent the cutoff values. The diagonal line is also drawn to show the distribution of the distances. By default, all outliers and leverage points are labeled with observation numbers. To change the default, you can use the LABEL= option as described in Table 83.5.

The residual-distance plot (RDPLOT) is used for both outlier and leverage-point diagnostics. It is a scatter plot of the standardized residuals against the robust distances. For more information about the robust distance, see the section Leverage Point and Outlier Detection. If a classification variable is specified in the model, this plot is not created.

You can use the PLOT=RDPLOT option to request this plot. The following statements use the growth data set in Example 83.2 to create a single plot, which is shown in Output 83.2.3 in Example 83.2:

ods graphics on;

proc quantreg data=growth ci=resampling plot=rdplot;
   model GDP = lgdp2 mse2 fse2 fhe2 mhe2 lexp2
               lintr2 gedy2 Iy2 gcony2 lblakp2 pol2 ttrad2
               / quantile=.5 diagnostics leverage(cutoff=8) seed=1268;
   id Country;
run;

The reference lines represent the cutoff values. By default, all outliers and leverage points are labeled with observation numbers. To change the default, you can use the LABEL= option as described in Table 83.5.

If you specify ID variables instead of observation numbers in the ID statement, the values of the first ID variable are used as labels.

PROC QUANTREG produces a histogram and a Q-Q plot for the standardized residuals. The histogram is superimposed with a normal density curve and a kernel density curve. Using the growth data set in Example 83.2, the following statements create the plot that is shown in Output 83.2.5 in Example 83.2:

ods graphics on;

proc quantreg data=growth ci=resampling plot=histogram;
   model GDP = lgdp2 mse2 fse2 fhe2 mhe2 lexp2
               lintr2 gedy2 Iy2 gcony2 lblakp2 pol2 ttrad2
               / quantile=.5 diagnostics leverage(cutoff=8) seed=1268;
   id Country;
run;