The ROBUSTREG Procedure
The PROC ROBUSTREG statement invokes the ROBUSTREG procedure. Table 86.1 summarizes the options available in the PROC ROBUSTREG statement.
Table 86.1: PROC ROBUSTREG Statement Options
|
Option |
Description |
|---|---|
|
Saves the estimated covariance matrix |
|
|
Specifies the input SAS data set |
|
|
Computes the final weighted least squares estimates |
|
|
Specifies an input SAS data set that contains initial estimates |
|
|
Displays the iteration history of the iteratively reweighted least squares algorithm |
|
|
Specifies the estimation method |
|
|
Specifies the length of effect names |
|
|
Specifies the order in which to sort classification variables |
|
|
Specifies an output SAS data set that contains the parameter estimates |
|
|
Specifies options that control details of the plots |
|
|
Specifies the seed for the random number generator |
You can specify the following options in the PROC ROBUSTREG statement.
- COVOUT
-
saves the estimated covariance matrix in the OUTEST= data set. This option is not supported for LTS estimation.
- DATA=SAS-data-set
-
specifies the input SAS data set to be used by PROC ROBUSTREG. By default, the most recently created SAS data set is used.
- FWLS
-
computes the final weighted least squares estimates. These estimates are equivalent to the least squares estimates after the detected outliers are deleted.
- INEST=SAS-data-set
-
specifies an input SAS data set that contains initial estimates for all the parameters in the model. For a detailed description of the contents of the INEST= data set, see the section INEST= Data Set.
- ITPRINT
-
displays the iteration history of the iteratively reweighted least squares algorithm that is used in M and MM estimation. You can also use this option in the MODEL statement.
- METHOD=method-type <(options)>
-
specifies the estimation method and some additional options for the estimation method. PROC ROBUSTREG provides four estimation methods: M estimation, LTS estimation, S estimation, and MM estimation. The default method is M estimation.
Note: Because the LTS and S methods use subsampling algorithms, these methods are not suitable in an analysis that uses variables that have only a few unequal values or a few unequal values within one BY group. For example, indicator variables that correspond to a classification variable often fall into this category. The same issue also applies to the initial LTS and S estimates in the MM method. For a model that includes classification independent variables or continuous independent variables with a few unequal values, the M method is recommended.
- NAMELEN=n
-
specifies the length of effect names in tables and output data sets to be n characters, where n is a value between 20 and 200. The default length is 20 characters.
- ORDER=DATA | FORMATTED | FREQ | INTERNAL
-
specifies the sort order for the levels of the classification variables (which are specified in the CLASS statement).
This option applies to the levels for all classification variables, except when you use the (default) ORDER=FORMATTED option with numeric classification variables that have no explicit format. In that case, the levels of such variables are ordered by their internal value.
The ORDER= option can take the following values:
Value of ORDER=
Levels Sorted By
DATA
Order of appearance in the input data set
FORMATTED
External formatted value, except for numeric variables with no explicit format, which are sorted by their unformatted (internal) value
FREQ
Descending frequency count; levels with the most observations come first in the order
INTERNAL
Unformatted value
By default, ORDER=FORMATTED. For ORDER=FORMATTED and ORDER=INTERNAL, the sort order is machine-dependent.
For more information about sort order, see the chapter on the SORT procedure in the Base SAS Procedures Guide and the discussion of BY-group processing in SAS Language Reference: Concepts.
- OUTEST=SAS-data-set
-
specifies an output SAS data set that contains the parameter estimates and, if the COVOUT option is specified, the estimated covariance matrix. For a detailed description of the contents of the OUTEST= data set, see the section OUTEST= Data Set.
-
PLOT | PLOTS <(global-plot-options)> <=plot-request>
PLOT | PLOTS <(global-plot-options)> <=(plot-request < …plot-request > )> -
specifies options that control details of the plots. If ODS Graphics is enabled but you do not specify the PLOTS= option, then PROC ROBUSTREG produces the robust fit plot by default when the model includes a single continuous independent variable.
ODS Graphics must be enabled before plots can be requested. For example:
ods graphics on; proc robustreg data=stack plots=all; model y = x1 x2 x3; run; ods graphics off;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
The global-plot-options apply to all plots that are generated by the ROBUSTREG procedure. The following global-plot-option is available:
You can specify more than one plot-request within the parentheses after PLOTS=. For a single plot-request, you can omit the parentheses. The following plot-requests are available:
- ALL
-
creates all appropriate plots.
- DDPLOT <(LABEL=ALL | LEVERAGE | NONE | OUTLIER)>
-
creates a plot of robust distance against Mahalanobis distance. For more information about robust distance, see the section Leverage-Point and Outlier Detection. The LABEL= option specifies how the points in this plot are to be labeled, as summarized in Table 86.2.
Table 86.2: Options for Label
Value of LABEL=
Label Method
ALL
Label all points
LEVERAGE
Label leverage points
NONE
No labels
OUTLIERS
Label outliers
By default, the ROBUSTREG procedure labels both outliers and leverage points.
If you specify ID variables in the ID statement, the values of the first ID variable are used as labels; otherwise, observation numbers are used as labels.
- FITPLOT <(NOLIMITS)>
-
creates a plot of robust fit against the single independent continuous variable that is specified in the model. You can request this plot when only a single independent continuous variable is specified in the model. Confidence limits are added to the plot by default. The NOLIMITS option suppresses these limits.
- HISTOGRAM
-
creates a histogram for the standardized robust residuals. The histogram is superimposed with a normal density curve and a kernel density curve.
- NONE
-
suppresses all plots.
- QQPLOT
-
creates the normal quantile-quantile plot for the standardized robust residuals.
- RDPLOT <(LABEL=ALL | LEVERAGE | NONE | OUTLIER)>
-
creates the plot of standardized robust residual against robust distance. For more information about robust distance, see the section Leverage-Point and Outlier Detection. The LABEL= option specifies a label method for points in this plot. These label methods are described in Table 86.2.
If you specify ID variables in the ID statement, the values of the first ID variable are used as labels; otherwise, observation numbers are used as labels.
- SEED=number
-
specifies the seed for the random number generator used to randomly select the subgroups and subsets for LTS and S estimation. By default, or if you specify 0, the ROBUSTREG procedure generates a random seed.
When you specify METHOD=M <(options)>, you can specify the following options:
- ASYMPCOV=H1 | H2 | H3
-
specifies the type of asymptotic covariance that is computed for the M estimate. The three types are described in the section Asymptotic Covariance and Confidence Intervals. By default, ASYMPCOV=H1.
- CONVERGENCE=criterion <(EPS=value)>
-
specifies a convergence criterion for the M estimate. Table 86.3 lists the three criteria that are available.
Table 86.3: Options to Specify Convergence Criteria
Type
Option
Coefficient
CONVERGENCE=COEF
Residual
CONVERGENCE=RESID
Weight
CONVERGENCE=WEIGHT
By default, CONVERGENCE=COEF. You can specify the precision of the convergence criterion by using the EPS= option; by default, EPS=1E–8.
- MAXITER=n
-
sets the maximum number of iterations during the parameter estimation. By default, MAXITER=1000.
- SCALE=scale-type | value
-
specifies the scale parameter or a method of estimating the scale parameter. These methods and options are summarized in Table 86.4.
Table 86.4: Options to Specify Scale
Scale
Option
Default d
Fixed constant
SCALE=value
Huber estimate
SCALE=HUBER <(D=d)>
2.5
Median estimate
SCALE=MED
Tukey estimate
SCALE=TUKEY <(D=d)>
2.5
By default, SCALE=MED.
-
WEIGHTFUNCTION=function-type
WF=function-type -
specifies the weight function that is used for the M estimate. The ROBUSTREG procedure provides 10 weight functions, which are listed in Table 86.5. You can specify the parameters in these functions by using the A=, B=, and C= options. These functions are described in the section M Estimation. The default weight function is bisquare.
Table 86.5: Options to Specify Weight Functions
Weight Function
Option
Default a, b, c
Andrews
WF=ANDREWS <(C=c)>
1.339
Bisquare
WF=BISQUARE <(C=c)>
4.685
Cauchy
WF=CAUCHY <(C=c)>
2.385
Fair
WF=FAIR <(C=c)>
1.4
Hampel
WF=HAMPEL <(<A=a> <B=b> <C=c>)>
2, 4, 8
Huber
WF=HUBER <(C=c)>
1.345
Logistic
WF=LOGISTIC <(C=c)>
1.205
Median
WF=MEDIAN <(C=c)>
0.01
Talworth
WF=TALWORTH <(C=c)>
2.795
Welsch
WF=WELSCH <(C=c)>
2.985
When you specify METHOD=LTS <(options)>, you can specify the following options:
- CSTEP=n
-
specifies the number of concentration steps (C-steps) for the LTS estimate. For information about how the default value is determined, see the section LTS Estimate.
- H=n
-
specifies the quantile for the LTS estimate. For information about how the default value is determined, see the section LTS Estimate
- IADJUST=ALL | NONE
-
requests (IADJUST=ALL) or suppresses (IADJUST=NONE) the intercept adjustment for all estimates in the LTS algorithm. By default, the intercept adjustment is used for data sets that contain fewer than 10,000 observations. For more information, see the section Algorithm.
- NBEST=n
-
specifies the number of best solutions that are kept for each subgroup during the computation of the LTS estimate. The default number is 10, which is the maximum number allowed.
- NREP=n
-
specifies the number of times to repeat least squares fit in subgroups during the computation of the LTS estimate. For information about how the default number is determined, see the section LTS Estimate.
- SUBANALYSIS
-
requests a display of the subgrouping information and parameter estimates within subgroups. This option generates the ODS tables that are listed in Table 86.6.
Table 86.6: ODS Tables Available with SUBANALYSIS Option
ODS Table Name
Description
BestEstimates
Best final estimates for LTS
BestSubEstimates
Best estimates for each subgroup
CStep
C-step information for LTS
Groups
Grouping information for LTS
- SUBGROUPSIZE=n
-
specifies the data set size of the subgroups in the computation of the LTS estimate. The default number is 300.
When you specify METHOD=S <(options)>, you can specify the following options:
- ASYMPCOV=H1 | H2 | H3 | H4
-
specifies the type of asymptotic covariance that is computed for the S estimate. The four types are described in the section Asymptotic Covariance and Confidence Intervals. By default, ASYMPCOV=H4.
- CHIF= TUKEY | YOHAI
-
specifies the
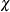 function for the S estimate. PROC ROBUSTREG provides two
function for the S estimate. PROC ROBUSTREG provides two 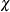 functions, Tukey’s bisquare function and Yohai’s optimal function, which you can request by specifying CHIF=TUKEY and CHIF=YOHAI,
respectively. The default is Tukey’s bisquare function.
functions, Tukey’s bisquare function and Yohai’s optimal function, which you can request by specifying CHIF=TUKEY and CHIF=YOHAI,
respectively. The default is Tukey’s bisquare function.
- EFF=value
-
specifies the efficiency (as a fraction) of the S estimate. The parameter
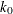 in the
in the 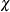 function is determined by this efficiency. The default efficiency is determined such that the consistent S estimate has a
breakdown value of 25%. This option is overwritten by the K0= option if both options are used.
function is determined by this efficiency. The default efficiency is determined such that the consistent S estimate has a
breakdown value of 25%. This option is overwritten by the K0= option if both options are used.
- K0=value
-
specifies the
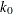 parameter in the
parameter in the 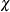 function of the S estimate. If you specify CHIF=TUKEY, the default is 1.548. If you specify CHIF=YOHAI, the default is 0.66. These default values correspond
to a 50% breakdown value of the consistent S estimate.
function of the S estimate. If you specify CHIF=TUKEY, the default is 1.548. If you specify CHIF=YOHAI, the default is 0.66. These default values correspond
to a 50% breakdown value of the consistent S estimate.
- MAXITER=n
-
sets the maximum number of iterations for computing the scale parameter of the S estimate. By default, MAXITER=1000.
- NREP=n
-
specifies the number of repeats of subsampling in the computation of the S estimate. For information about how the default number of repeats is determined, see the section Algorithm.
- NOREFINE
-
suppresses the refinement of the S estimate. For more information, see the section Algorithm.
- SUBSETSIZE=n
-
specifies the size of the subset for the S estimate. For information about how the default value is determined, see the section Algorithm.
- TOLERANCE=value
-
specifies the tolerance for the S estimate of the scale. The default value is 0.001.
When you specify METHOD=MM <(options)>, you can specify the following options:
- ASYMPCOV=H1 | H2 | H3 | H4
-
specifies the type of asymptotic covariance that is computed for the MM estimate. The four types are described in the section Details: ROBUSTREG Procedure. By default, ASYMPCOV=H4.
- BIASTEST <(ALPHA=number)>
-
requests the bias test for the final MM estimate. For more information about this test, see the section Bias Test.
- CHIF=TUKEY | YOHAI
-
selects the
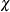 function for the MM estimate. PROC ROBUSTREG provides two
function for the MM estimate. PROC ROBUSTREG provides two 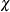 functions, Tukey’s bisquare function and Yohai’s optimal function, which you can request by specifying CHIF=TUKEY and CHIF=YOHAI,
respectively. The default is Tukey’s bisquare function. This
functions, Tukey’s bisquare function and Yohai’s optimal function, which you can request by specifying CHIF=TUKEY and CHIF=YOHAI,
respectively. The default is Tukey’s bisquare function. This 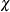 function is also used by the initial S estimate if you specify the INITEST=S option.
function is also used by the initial S estimate if you specify the INITEST=S option.
- CONVERGENCE=criterion <(EPS=number)>
-
specifies a convergence criterion for the MM estimate. Table 86.7 lists the three criteria that are available.
Table 86.7: Options to Specify Convergence Criteria
Type
Option
Coefficient
CONVERGENCE=COEF
Residual
CONVERGENCE=RESID
Weight
CONVERGENCE=WEIGHT
By default, CONVERGENCE=COEF. You can specify the precision of the convergence criterion by using the EPS= option; by default, EPS=1E–8.
- EFF=value
-
specifies the efficiency (as a fraction) of the MM estimate. The parameter
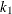 in the
in the 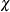 function is determined by this efficiency. The default efficiency is set to 0.85, which corresponds to
function is determined by this efficiency. The default efficiency is set to 0.85, which corresponds to 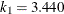 if you specify CHIF=TUKEY or
if you specify CHIF=TUKEY or 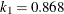 if you specify CHIF=YOHAI.
if you specify CHIF=YOHAI.
- INITEST=LTS | S
-
specifies the initial estimator for the MM estimator. By default, the LTS estimator with its default settings is used as the initial estimator for the MM estimator.
- INITH=h
-
specifies the integer h for the initial LTS estimate that is used by the MM estimator. For information about how to specify h and how the default is determined, see the section Algorithm.
- K0=number
-
specifies the parameter
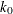 in the
in the 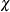 function for the MM estimate. If you specify CHIF=TUKEY, the default is
function for the MM estimate. If you specify CHIF=TUKEY, the default is 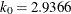 . If you specify CHIF=YOHAI, the default is
. If you specify CHIF=YOHAI, the default is 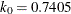 . These default values correspond to the 25% breakdown value of the MM estimator.
. These default values correspond to the 25% breakdown value of the MM estimator.
- MAXITER=n
-
sets the maximum number of iterations during the parameter estimation. By default, MAXITER=1000.
