The COPULA Procedure

Dependence Measures

There are three basic types of measures: linear correlation, rank correlation, and tail dependence. Linear correlation is given by

\[ \rho \equiv \textrm{corr}(X,Y)= \frac{\textrm{cov}(X,Y)}{\sqrt {\textrm{var}(X)}\sqrt {\textrm{var}(Y)}} \]

The linear correlation coefficient carries very limited information about the joint properties of the variables. A well-known property is that uncorrelatedness does not imply independence, while independence implies noncorrelation. In addition, there exist distinct bivariate distributions that have the same marginal distribution and the same correlation coefficient. These results suggest that caution must be used when interpreting the linear correlation.

Another statistical measure of dependence is called rank correlation, which is nonparametric. Kendall’s tau, for example, is the covariance between the sign statistic $X_1-\tilde{X}_1$ and $X_2-\tilde{X}_2$, where $(\tilde{X}_1,\tilde{X}_2)$ is an independent copy of $(X_1,X_2)$:

\[ \rho _\tau \equiv E[\textrm{sign}(X_1 -\tilde{X}_1)(X_2 -\tilde{X}_2)] \]

The sign function (sometimes written as sgn) is defined by

\[ \textrm{sign}(x)= \begin{cases} -1 & \mr{if } x \le 0 \\ 0 & \mr{if } x = 0 \\ 1 & \mr{if } x \ge 0 \end{cases} \]

Spearman’s rho is the correlation between the transformed random variables:

\[ \rho _ S(X_1,X_2) \equiv \rho (F_1(X_1),F_2(X_2)) \]

The variables are transformed by their distribution functions so that the transformed variables are uniformly distributed on $[0,1]$. The rank correlations depend only on the copula of the random variables and are indifferent to the marginal distributions. Like linear correlation, the rank correlations have their limitations. In particular, there are different copulas that result in the same rank correlation.

A third measure focuses on only part of the joint properties between the variables. Tail dependence measures the dependence when both variables are at extreme values. Formally, they can be defined as the conditional probabilities of quantile exceedances. There are two types of tail dependence:

  • The upper tail dependence, denoted 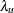$\lambda _ u$, is

    \[ \lambda _ u(X_1,X_2) \equiv \lim _{q->1^-} P(X_2> F_2^{-1}(q)|X_1>F_1^{-1}(q)) \]

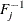    when the limit exists $\lambda _ u \in [0,1]$. Here $F_ j^{-1}$ is the quantile function (that is, the inverse of the CDF).

  • The lower tail dependence is defined symmetrically.

Tail dependence is hard to detect by looking at a scatter plot of realizations of two random variables. One graphical way to detect tail dependence between two variables is by creating the chi plot of those two variables. The chi plot, as defined in Fisher and Switzer (2001), has characteristic patterns that depend on the dependence structure between the variables. The chi plot for the random variables $X$ and $Y$ is a scatter plot of the pairs $(\lambda _ i,\chi _ i)$ for each data point $(x_ i, y_ i)$. $\lambda _ i$ is a measure of the distance of the data point $(x_ i, y_ i)$ from the center of the data as measured by the median values of $(x_ i, y_ i)$, and $\chi _ i$ is a correlation coefficient between dichotomized values of $X$ and $Y$. A positive $\lambda _ i$ means that $x_ i$ and $y_ i$ are either both large with respect to their median values or both small. A negative $\lambda _ i$ means that $x_ i$ or $y_ i$ is large with respect to its median, whereas the other value is small. Signs of tail dependence manifest as clusters of points that are significantly far from the $\chi $ axis around $\lambda $ values of $\pm $1. If $X$ and $Y$ are uncorrelated, the $\chi $ values cluster around the $\lambda $ axis.