The COPULA Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasHierarchical Archimedean Copula (HAC)Canonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names
Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasHierarchical Archimedean Copula (HAC)Canonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names -
Examples

- References
Adopting the notations of Savu and Trede (2010), let ![]() denote the total level of hierarchies and let
denote the total level of hierarchies and let ![]() denote the dimension of the HAC. There are
denote the dimension of the HAC. There are ![]() distinct copulas at each level
distinct copulas at each level ![]() . These copulas are indexed by
. These copulas are indexed by ![]() . At each level, there are also
. At each level, there are also ![]() variables,
variables, ![]() and
and ![]() . In the first step, all the variables at the lowest level are grouped into
. In the first step, all the variables at the lowest level are grouped into ![]() subsets, each subset being an ordinary multivariate Archimedean copula
subsets, each subset being an ordinary multivariate Archimedean copula
where ![]() is the generator of copula
is the generator of copula ![]() ,
, ![]() denotes the variables that belong to copula
denotes the variables that belong to copula ![]() , and the sum
, and the sum ![]() is the sum over each variable in the subset
is the sum over each variable in the subset ![]() . The copulas
. The copulas ![]() can be different Archimedean copulas for
can be different Archimedean copulas for ![]() . Then at the second level, the copulas
. Then at the second level, the copulas ![]() that are derived in the first level are aggregated as if they are individual variables. Suppose there are
that are derived in the first level are aggregated as if they are individual variables. Suppose there are ![]() copulas and
copulas and ![]() variables,
variables,
![\[ C_{2,j}(\bm {C}_{1,j},\bm {u}_{2,j}) =\phi _{2,j}^{-1}\left(\sum _{\bm {C}_{1,j}} \phi _{2,j}(\bm {C}_{1,j})+\sum _{\bm {u}_{2,j}} \phi _{2,j}(\bm {u}_{2,j})\right) \]](images/etsug_copula0220.png)
where ![]() denotes the generator of
denotes the generator of ![]() and
and ![]() represents the subset of copulas in
represents the subset of copulas in ![]() , that is aggregated for copula
, that is aggregated for copula ![]() for
for ![]() . This structure continues until at level
. This structure continues until at level ![]() a single copula
a single copula ![]() aggregates all the copulas at its previous level,
aggregates all the copulas at its previous level, ![]() .
.
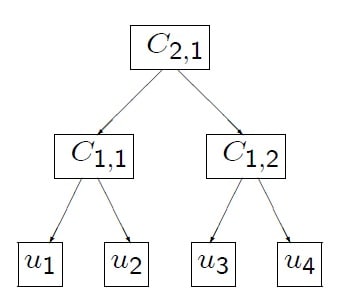
A four-dimensional example that has total levels ![]() and a structure shown in Figure 10.5 is defined as follows:
and a structure shown in Figure 10.5 is defined as follows:
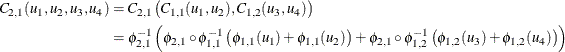
Theorem 4.4 of McNeil (2008) states that the sufficient condition for a general hierarchical Archimedean structure to be a proper copula is that all
appearing nodes of the form ![]() have completely monotone derivatives. This condition places certain constraints on the copula parameters. In particular,
if all the copulas in a hierarchical structure come from the Frank, Clayton, or Gumbel family, then
have completely monotone derivatives. This condition places certain constraints on the copula parameters. In particular,
if all the copulas in a hierarchical structure come from the Frank, Clayton, or Gumbel family, then ![]() for all j when
for all j when ![]() . Intuitively, this means that rank correlation must be increasing as you move down the hierarchical structure.
. Intuitively, this means that rank correlation must be increasing as you move down the hierarchical structure.
The hierarchical Archimedean copulas available in the COPULA procedure are the hierarchical versions of the Clayton, Frank, and Gumbel copulas.
A slightly modified version of the recursive algorithm from McNeil (2008) works for all valid hierarchical structures that have Clayton, Frank, or Gumbel generators:
-
Start at
 , and generate a random variable
, and generate a random variable  with the distribution function
with the distribution function 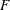 with Laplace transform
with Laplace transform 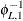 .
.
-
For
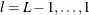 , generate
, generate 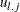 from its parent hierarchy. For
from its parent hierarchy. For 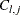 , recursively call this algorithm with the proper inner generators that correspond to the copula family.
, recursively call this algorithm with the proper inner generators that correspond to the copula family.
-
Return
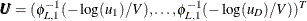 .
.
Let ![]() be the outer generator and
be the outer generator and ![]() the nested generator, and let
the nested generator, and let ![]() and
and ![]() be the respective generator parameters. Let v be a draw from distribution function
be the respective generator parameters. Let v be a draw from distribution function ![]() with Laplace transform
with Laplace transform ![]() . The inner copula generators
. The inner copula generators ![]() and their corresponding Laplace transform distributions for the Clayton, Frank, and Gumbel family are summarized in Table 10.3.
and their corresponding Laplace transform distributions for the Clayton, Frank, and Gumbel family are summarized in Table 10.3.
Table 10.3: Inner Generators and Corresponding Distributions
|
Copula Type |
|
Distribution with LT |
|---|---|---|
|
Clayton |
|
Tiled stable |
|
Gumbel |
|
Stable |
|
Frank |
|
No closed form |
Note that when ![]() , the inner generators for the Clayton and Gumbel family both simplify to the generator of the independence copula,
, the inner generators for the Clayton and Gumbel family both simplify to the generator of the independence copula, ![]() . For more information about simulating from the distribution with the Laplace transform given by the inner generator for
the Frank family, see Hofert (2011). For more information about how to simulate from a tilted stable distribution, see McNeil (2008).
. For more information about simulating from the distribution with the Laplace transform given by the inner generator for
the Frank family, see Hofert (2011). For more information about how to simulate from a tilted stable distribution, see McNeil (2008).