The COUNTREG Procedure

Bayesian Analysis

Subsections:

To perform Bayesian analysis, you must specify a BAYES statement. Unless otherwise stated, all options in this section are options in the BAYES statement.

By default, PROC COUNTREG uses the random walk Metropolis algorithm to obtain posterior samples. For information about implementing the Metropolis algorithm in PROC COUNTREG, such as blocking the parameters and tuning the covariance matrices, see the sections Blocking of Parameters and Tuning the Proposal Distribution.

The Bayes theorem states that

\begin{equation*} p(\theta | \mb{y})\propto \pi (\theta ) L(y|\theta ) \end{equation*}

where $\theta $ is a parameter or a vector of parameters and $\pi (\theta )$ is the product of the prior densities that are specified in the PRIOR statement. The term $L(y|\theta )$ is the likelihood that is associated with the MODEL statement.

Blocking of Parameters

In a multivariate parameter model, all the parameters are updated in one single block (by default or when you specify the SAMPLING=MULTIMETROPOLIS option). This could be inefficient, especially when parameters have vastly different scales. As an alternative, you could update the parameters one at a time (by specifying SAMPLING=UNIMETROPOLIS).

Tuning the Proposal Distribution

One key factor in achieving high efficiency of a Metropolis-based Markov chain is finding a good proposal distribution for each block of parameters. This process is called tuning. The tuning phase consists of a number of loops that are controlled by the options MINTUNE= and MAXTUNE=. The MINTUNE= option controls the minimum number of tuning loops and has a default value of 2. The MAXTUNE= option controls the maximum number of tuning loops and has a default value of 24. Each loop iterates the number of times that are specified by the NTU= option, which has a default of 500. At the end of every loop, PROC COUNTREG examines the acceptance probability for each block. The acceptance probability is the percentage of samples, specified by the NTU= option, that have been accepted. If this probability does not fall within the acceptable tolerance range (see the following section), the proposal distribution is modified before the next tuning loop begins.

A good proposal distribution should resemble the actual posterior distribution of the parameters. Large sample theory states that the posterior distribution of the parameters approaches a multivariate normal distribution (see Gelman et al. 2004, Appendix B; Schervish 1995, Section 7.4). That is why a normal proposal distribution often works well in practice. The default proposal distribution in PROC COUNTREG is the normal distribution.

Scale Tuning

The acceptance rate is closely related to the sampling efficiency of a Metropolis chain. For a random walk Metropolis, a high acceptance rate means that most new samples occur right around the current data point. Their frequent acceptance means that the Markov chain is moving rather slowly and not exploring the parameter space fully. A low acceptance rate means that the proposed samples are often rejected; hence the chain is not moving much. An efficient Metropolis sampler has an acceptance rate that is neither too high nor too low. The scale c in the proposal distribution $q(\cdot | \cdot )$ effectively controls this acceptance probability. Roberts, Gelman, and Gilks (1997) show that if both the target and proposal densities are normal, the optimal acceptance probability ($\text {TargetAcceptance}$) for the Markov chain should be around 0.45 in a one-dimensional problem and should asymptotically approach 0.234 in higher-dimensional problems. The corresponding optimal scale is 2.38, which is the initial scale that is set for each block.

Because of the nature of stochastic simulations, it is impossible to fine-tune a set of variables so that the Metropolis chain has exactly the desired acceptance rate that you want. In addition, Roberts and Rosenthal (2001) empirically demonstrate that an acceptance rate between 0.15 and 0.5 is at least 80% efficient, so there is really no need to fine-tune the algorithms to reach an acceptance probability that is within a small tolerance of the optimal values. PROC COUNTREG works with a probability range, determined by $\text {TargetAcceptance}\pm 0.075$. If the observed acceptance rate in a given tuning loop is less than the lower bound of the range, the scale is reduced; if the observed acceptance rate is greater than the upper bound of the range, the scale is increased. During the tuning phase, a scale parameter in the normal distribution is adjusted as a function of the observed acceptance rate and the target acceptance rate. PROC COUNTREG uses the updating scheme[1]

\[ c_{\mbox{new}} =\frac{ c_{\mbox{cur}} \cdot \Phi ^{-1}( p_{\mbox{opt}}/2) }{ \Phi ^{-1}( p_{ \mbox{cur}}/2) } \]

where $c_{\mbox{cur}}$ is the current scale, $p_{\mbox{cur}}$ is the current acceptance rate, and $p_{\mbox{opt}}$ is the optimal acceptance probability.

Covariance Tuning

To tune a covariance matrix, PROC COUNTREG takes a weighted average of the old proposal covariance matrix and the recent observed covariance matrix, based on the number of samples (as specified by the NTU= option) in the current loop. The formula to update the covariance matrix is

\[ \mbox{COV}_{\mbox{new}} = 0.75 ~ \mbox{COV}_{\mbox{cur}} + 0.25 ~ \mbox{COV}_{\mbox{old}} \]

There are two ways to initialize the covariance matrix:

  • The default is an identity matrix that is multiplied by the initial scale of 2.38 and divided by the square root of the number of estimated parameters in the model. A number of tuning phases might be required before the proposal distribution is tuned to its optimal stage, because the Markov chain needs to spend time learning about the posterior covariance structure. If the posterior variances of your parameters vary by more than a few orders of magnitude, if the variances of your parameters are much different from 1, or if the posterior correlations are high, then the proposal tuning algorithm might have difficulty forming an acceptable proposal distribution.

  • Alternatively, you can use a numerical optimization routine, such as the quasi-Newton method, to find a starting covariance matrix. The optimization is performed on the joint posterior distribution, and the covariance matrix is a quadratic approximation at the posterior mode. In some cases this is a better and more efficient way of initializing the covariance matrix. However, there are cases, such as when the number of parameters is large, in which the optimization could fail to find a matrix that is positive definite. In those cases, the tuning covariance matrix is reset to the identity matrix.

A by-product of the optimization routine is that it also finds the maximum a posteriori (MAP) estimates with respect to the posterior distribution. The MAP estimates are used as the initial values of the Markov chain.

For more information, see the section INIT Statement.

Initial Values of the Markov Chains

You can assign initial values to any parameters. (For more information, see the section INIT Statement) If you use the optimization option PROPCOV= , then PROC COUNTREG starts the tuning at the optimized values. This option overwrites the provided initial values. If you specify the RANDINIT option, the information that the INIT statement provides is overwritten.

Aggregation of Multiple Chains

When you want to exploit the possibility of running several MCMC instances at the same time (that is, the value of the NTRDS= option is greater than 1), you face the problem of aggregating the chains. In ordinary applications, each MCMC instance can easily obtain stationary samples from the entire posterior distribution. In these applications, you can use the option AGGREGATION=NOWEIGHTED. This option piles one chain on top of another and makes no particular adjustment. However, when the posterior distribution is characterized by multiple distinct posterior modes, some of the MCMC instances fail to obtain stationary samples from the entire posterior distribution. You can use the option AGGREGATION=WEIGHTED when the posterior samples from each MCMC instance approximate well only a part of the posterior distribution.

The main idea behind the option AGGREGATION=WEIGHTED is to consider the entire posterior distribution to be similar to a mixture distribution. When you are sampling with multiple threads, each MCMC instance samples from one of the mixture components. Then the samples from each mixture component are aggregated together using a resampling scheme in which weights are proportional to the nonnormalized posterior distribution.

Description of the Algorithm

The preliminary step of the aggregation that is implied by the option AGGREGATION=WEIGHTED is to run several ($K$) independent instances of the MCMC algorithm. Each instance searches for a set of stationary samples. Notice that the concept of stationarity is weaker: each instance might be able to explore not the entire posterior but only portions of it. In the following, each column represents the output from one MCMC instance:

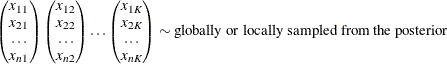
\begin{equation*} \begin{pmatrix} x_{11} \\ x_{21} \\ \ldots \\ x_{n1} \end{pmatrix}\begin{pmatrix} x_{12} \\ x_{22} \\ \ldots \\ x_{n2} \end{pmatrix} \ldots \begin{pmatrix} x_{1K} \\ x_{2K} \\ \ldots \\ x_{nK} \end{pmatrix} \sim \text {globally or locally sampled from the posterior} \end{equation*}

If the length of each chain is less than n, you can augment the corresponding chain by subsampling the chain itself. Each chain is then sorted with respect to the nonnormalized posterior density: $\pi (x_{[1].})\leq \pi (x_{[2].})\leq \cdots \pi (x_{[n].})$. Therefore,

\begin{equation*} \begin{pmatrix} x_{11} \\ x_{21} \\ \ldots \\ x_{n1} \end{pmatrix}\begin{pmatrix} x_{12} \\ x_{22} \\ \ldots \\ x_{n2} \end{pmatrix} \ldots \begin{pmatrix} x_{1K} \\ x_{2K} \\ \ldots \\ x_{nK} \end{pmatrix} \rightarrow \begin{pmatrix} x_{[1]1} \\ x_{[2]1} \\ \ldots \\ x_{[n]1} \end{pmatrix}\begin{pmatrix} x_{[1]2} \\ x_{[2]2} \\ \ldots \\ x_{[n]2} \end{pmatrix} \ldots \begin{pmatrix} x_{[1]K} \\ x_{[2]K} \\ \ldots \\ x_{[n]K} \end{pmatrix}\end{equation*}

The final step is to use a multinomial sampler to resample each row i with weights proportional to the nonnormalized posterior densities:

\begin{equation*} \widetilde{x}_{(i-1)K+1},\widetilde{x}_{(i-1)K+2},\ldots ,\widetilde{x}_{(i-1)K+K}\sim \mr{Multinom}\left[x_{[i]1},x_{[i]2},\ldots ,x_{[i]K};\pi (x_{[i]1}), \pi (x_{[i]2}),\ldots ,\pi (x_{[i]K})\right] \end{equation*}

The resulting posterior sample,

\begin{equation*} \widetilde{x}_{1},\widetilde{x}_{2},\ldots ,\widetilde{x}_{K},\ldots ,\widetilde{x}_{(i-1)K+1},\widetilde{x}_{(i-1)K+2},\ldots ,\widetilde{x}_{(i-1)K+K}, \ldots ,\widetilde{x}_{(n-1)K+1},\widetilde{x}_{(n-1)K+2},\ldots ,\widetilde{x}_{nK} \end{equation*}

is a good approximation of the posterior distribution that is characterized by multiple modes.

Automated Initialization of MCMC

The MCMC methods can generate samples from the posterior distribution. The correct implementation of these methods often requires the stationarity analysis, convergence analysis, and accuracy analysis of the posterior samples. These analyses usually imply the following:

  • initialization of the proposal distribution

  • initialization of the chains (starting values)

  • determination of the burn-in

  • determination of the length of the chains

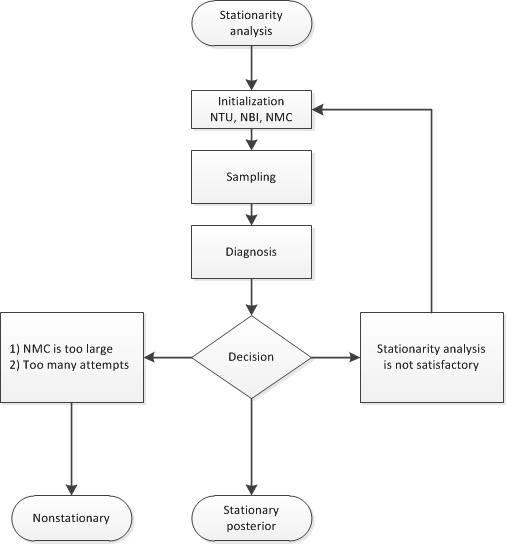
In more general terms, this determination is equivalent to deciding whether the samples are drawn from the posterior distribution (stationarity analysis) and whether the number of samples is large enough to accurately approximate the posterior distribution (accuracy analysis). You can use the AUTOMCMC option to automate and facilitate the stationary analysis and the accuracy analysis.

Description of the Algorithm

The algorithm has two phases. In the first phase, the stationarity phase, the algorithm tries to generate stationary samples from the posterior distribution. In the second phase, the accuracy phase, the algorithm searches for an accurate representation of the posterior distribution. The algorithm implements the following tools:

  • Geweke test to check stationarity

  • Heidelberger-Welch test to check stationarity and provide a proxy for the burn-in

  • Heidelberger-Welch halfwidth test to check the accuracy of the posterior mean

  • Raftery-Lewis test to check the accuracy of a specified percentile (indirectly providing a proxy for the number of required samples)

  • effective sample size analysis to determine a proxy for the number of required samples

During the stationarity phase, the algorithm searches for stationarity. The number of attempts that the algorithm makes is determined by the ATTEMPTS= option. During each attempt, a preliminary tuning stage chooses a proposal distribution for the MCMC sampler. At the end of the preliminary tuning phase, the algorithm analyzes tests for the stationarity of the samples. If the percentage of successful stationary tests is greater than or equal to the percentage that is indicated by the TOL= option, then the posterior sample is considered to be stationary. If the sample cannot be considered stationary, then the algorithm attempts to achieve stationarity by changing some of the initialization parameters as follows:

  • increasing the number of tuning samples (NTU= option)

  • increasing the number of posterior samples (NMC= option)

  • increasing the burn-in (NBI= option)

Figure 11.6 shows a flowchart of the AUTOMCMC algorithm as it searches for stationarity.

Figure 11.6: Flowchart of the AUTOMCMC Algorithm: Stationarity Analysis

Flowchart of the AUTOMCMC Algorithm: Stationarity Analysis


You can initialize NMC=M, NBI=B, and NTU=T during the stationarity phase by specifying the NMC=, NBI=, and NTU= options in the BAYES statement. You can also change the minimum stationarity acceptance ratio of successful stationarity tests that are needed to exit the stationarity phase. By default, TOL=0.95. For example: 

   proc countreg data=dataset;
      ...;
      bayes nmc=M nbi=B ntu=T automcmc=( stationarity=(tol=0.95) );
      ...;
   run;

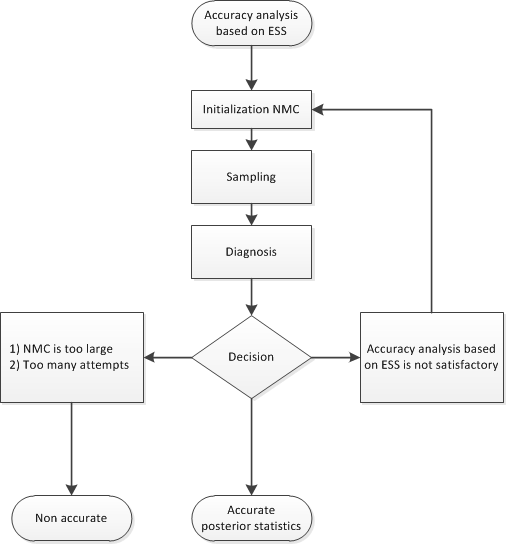
During the accuracy phase, the algorithm attempts to determine how many posterior samples are needed. The number of attempts is determined by the ATTEMPTS= option. You can choose between two different approaches to study the accuracy:

  • accuracy analysis based on the effective sample size (ESS)

  • accuracy analysis based on the Heidelberger-Welch halfwidth test and the Raftery-Lewis test

If you choose the effective sample size approach, you must provide the minimum number of effective samples that are needed. You can also change the tolerance for the ESS accuracy analysis (by default, TOL=0.95). For example: 

   proc countreg data=dataset;
      ...;
      bayes automcmc=(targetess=N accuracy=(tol=0.95));
      ...;
   run;

Figure 11.7 shows a flowchart of the AUTOMCMC algorithm based on the effective sample size approach to determine whether the samples provide an accurate representation of the posterior distribution.

Figure 11.7: Flowchart of the AUTOMCMC Algorithm: Accuracy Analysis Based on the ESS

Flowchart of the AUTOMCMC Algorithm: Accuracy Analysis Based on the ESS


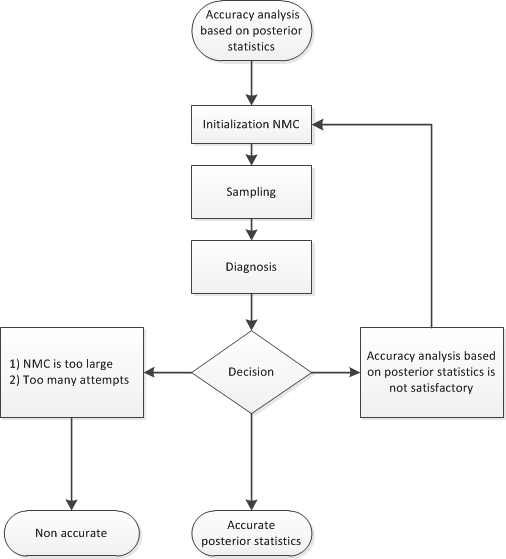
If you choose the accuracy analysis based on the Heidelberger-Welch halfwidht test and the Raftery-Lewis test (the default option), then you might want to choose a posterior quantile of interest for the Raftery-Lewis test (by default, 0.025). You can also change the tolerance for the accuracy analysis (by default, TOL=0.95). Notice that the Raftery-Lewis test produces a proxy for the number of posterior samples that are required. In each attempt, the current number of posterior samples is compared to this proxy. If the proxy is greater than the current NMC, then the algorithm reinitializes itself. To control this reinitialization, you can use the option RLLIMITS=(LB=lb UB=ub). In particular, there are three cases

  • If the proxy is greater than ub, then NMC is set equal to ub.

  • If the proxy is less than lb, then NMC is set equal to lb.

  • If lb is less than the proxy, which is less than ub, then NMC is set equal to the proxy.

For example: 

   proc countreg data=dataset;
      ...;
      bayes raftery(q=0.025) automcmc=( accuracy=(tol=0.95 targetstats=(rllimits=(lb=k1 ub=k2))) );
      ...;
   run;

Figure 11.8 shows a flowchart of the AUTOMCMC algorithm based on the Heidelberger-Welch halfwidth test and the Raftery-Lewis test approach to determine whether the posterior samples provide an accurate representation of the posterior distribution.

Figure 11.8: Flowchart of the AUTOMCMC Algorithm: Accuracy Analysis Based on the Heidelberger-Welch Halfwidth Test and the Raftery-Lewis Test

Flowchart of the AUTOMCMC Algorithm: Accuracy Analysis Based on the Heidelberger-Welch Halfwidth Test and the Raftery-Lewis Test



[1] Roberts, Gelman, and Gilks (1997) and Roberts and Rosenthal (2001) demonstrate that the relationship between acceptance probability and scale in a random walk Metropolis scheme is $p =2\Phi \left( -\sqrt {I} c /2\right)$, where $c $ is the scale, p is the acceptance rate, $\Phi $ is the CDF of a standard normal, and $I\equiv E_{f}[ ( f^{\prime } (x) /f (x) ) ^{2} ] $, $ f\left( x\right) $ is the density function of samples (Roberts, Gelman, and Gilks, 1997; Roberts and Rosenthal, 2001). This relationship determines the updating scheme, with I replaced by the identity matrix to simplify calculation.