The COUNTREG Procedure
- Overview
- Getting Started
-
Syntax
 Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSTORE StatementWEIGHT StatementZEROMODEL Statement
Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSTORE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics
Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics -
Examples

- References
The data set DocVisit contains information for approximately 5,000 Australian individuals about the number and possible determinants of doctor
visits that were made during a two-week interval. This data set contains a subset of variables that are taken from the Racd3 data set used by Cameron and Trivedi (1998). The DocVisit data set can be found in the SAS/ETS Sample Library.
The variable Doctorco represents doctor visits. Additional variables in the data set that you want to evaluate as determinants of doctor visits
include Sex (coded 0=male, 1=female), Age (age in years divided by 100), Illness (number of illnesses during the two-week interval, with five or more coded as five), Income (annual income in Australian dollars divided by 1,000), and Hscore (a score on a general health questionnaire, in which a high score indicates bad health). Summary statistics for these variables
are computed in the following statements and presented in Output 11.1.1.
proc means data=docvisit; var doctorco sex age illness income hscore; run;
Output 11.1.1: Summary Statistics
| Variable | N | Mean | Std Dev | Minimum | Maximum | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
The following statements fit a Poisson model to the data by using the covariates Sex, Illness, Income, and Hscore:
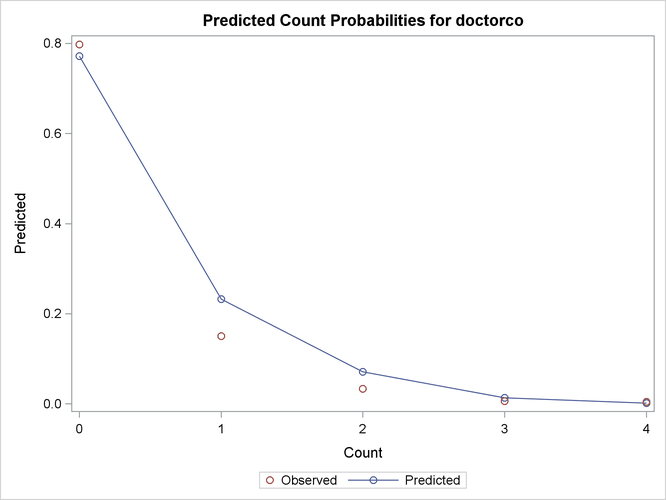
proc countreg data=docvisit plots(only counts(0 to 4 by 1))=(predprob predpro); model doctorco=sex illness income hscore / dist=poisson printall; run;
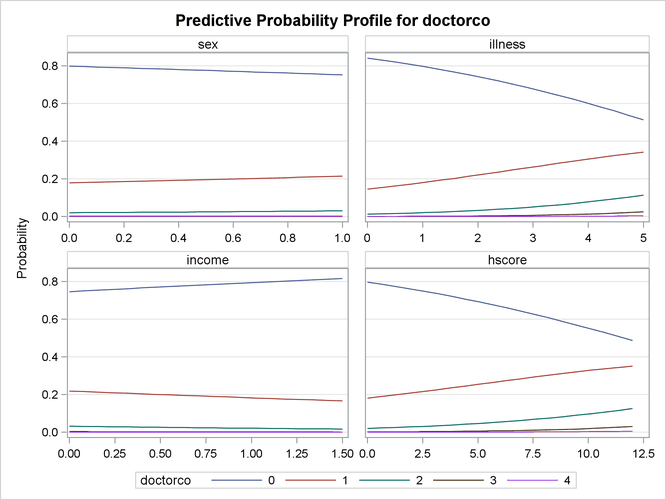
Output 11.1.2 shows the predicted probabilities of count levels 0 to 4 from the Poisson model. Most of the observed counts are in the range 0 to 4 and account for more than 99% of the entire data set. One factor that would be interesting to explore is how the model-predicted probabilities of those count levels react to different regressor values. Output 11.1.3 shows the predictive profiles of the count levels in question against the first three regressors in the model. In each panel, the regressor in question is varied while all other regressors are fixed at their observed mean and the model parameters are fixed at their MLE.
In this example, the DIST= option in the MODEL statement specifies the Poisson distribution. In addition, the PRINTALL option displays the correlation and covariance matrices for the parameters, log-likelihood values, and convergence information in addition to the parameter estimates. The parameter estimates for this model are shown in Output 11.1.4.
If some regressors are categorical in nature (meaning that these variables can take only a few discrete qualitative values),
specify them in the CLASS statement. In this example, Sex is categorical because it takes only two values. A CLASS variable can be numeric or character.
Consider the following extension:
proc countreg data=docvisit; class sex; model doctorco=sex illness income hscore / dist=poisson; run;
The partial output is given in Output 11.1.5.
Output 11.1.5: Parameter Estimates of Poisson Model with CLASS statement
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| Intercept | 1 | -1.619969 | 0.063985 | -25.32 | <.0001 |
| sex 0 | 1 | -0.235583 | 0.054362 | -4.33 | <.0001 |
| sex 1 | 0 | 0 | . | . | . |
| illness | 1 | 0.270326 | 0.017080 | 15.83 | <.0001 |
| income | 1 | -0.242095 | 0.077829 | -3.11 | 0.0019 |
| hscore | 1 | 0.096313 | 0.009089 | 10.60 | <.0001 |
If the CLASS statement is present, the COUNTREG procedure creates as many indicator or dummy variables as there are categories
in a CLASS variable and uses them as independent variables. In order to avoid collinearity with the intercept, the last-created
dummy variable is assigned a zero coefficient by default. This means that only the dummy variable that is associated with
the first level of Sex (male=0) is used as a regressor. Consequently, the estimated coefficient for this dummy variable is the negative of the one
for the original Sex variable in Output 11.1.4, because the reference level has switched from male to female.
Now consider a more practical task. The previous example implicitly assumes that each additional illness during the two-week
interval has the same effect. In other words, this variable is thought of as a continuous variable. But this variable has
only six values, and it is quite possible that the number of illnesses has a nonlinear effect on doctor visits. In order to
check this conjecture, the following statements specify the Illness variable in the CLASS statement so that it is represented in the model by a set of six dummy variables that can account for
any type of nonlinearity:
proc countreg data=docvisit; class sex illness; model doctorco=sex illness income hscore / dist=poisson; run;
The parameter estimates are displayed in Output 11.1.6.
Output 11.1.6: Parameter Estimates of Poisson Model with CLASS statement
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| Intercept | 1 | -0.385930 | 0.088062 | -4.38 | <.0001 |
| sex 0 | 1 | -0.219118 | 0.054190 | -4.04 | <.0001 |
| sex 1 | 0 | 0 | . | . | . |
| illness 0 | 1 | -1.934983 | 0.121267 | -15.96 | <.0001 |
| illness 1 | 1 | -0.698307 | 0.089732 | -7.78 | <.0001 |
| illness 2 | 1 | -0.471100 | 0.090742 | -5.19 | <.0001 |
| illness 3 | 1 | -0.488481 | 0.099127 | -4.93 | <.0001 |
| illness 4 | 1 | -0.272372 | 0.107593 | -2.53 | 0.0114 |
| illness 5 | 0 | 0 | . | . | . |
| income | 1 | -0.253583 | 0.077441 | -3.27 | 0.0011 |
| hscore | 1 | 0.094590 | 0.009025 | 10.48 | <.0001 |
The Estimate column shows the difference between each ILLNESS parameter and ILLNESS=5. Note that these estimates for different
Illness categories do not increase linearly but instead show a relatively large jump from zero illnesses to one illness, followed
by relatively smaller increases.
Suppose you suspect that the population of individuals can be viewed as two distinct groups: a low-risk group, consisting
of individuals who never go to the doctor, and a high-risk group, consisting of individuals who do go to the doctor. You might
suspect that the data have this structure both because the sample variance of Doctorco (0.64) exceeds its sample mean (0.30), which suggests overdispersion, and because a large fraction of the Doctorco observations (80%) have the value zero. Estimating a zero-inflated model is one way to deal with overdispersion that results
from excess zeros.
Suppose also that you suspect that the covariate Age has an impact on whether an individual belongs to the low-risk group. For example, younger individuals might have illnesses
of much lower severity when they do get sick and be less likely to visit a doctor, all other factors being equal. The following
statements estimate a zero-inflated Poisson regression, with Age as a covariate in the zero-generation process:
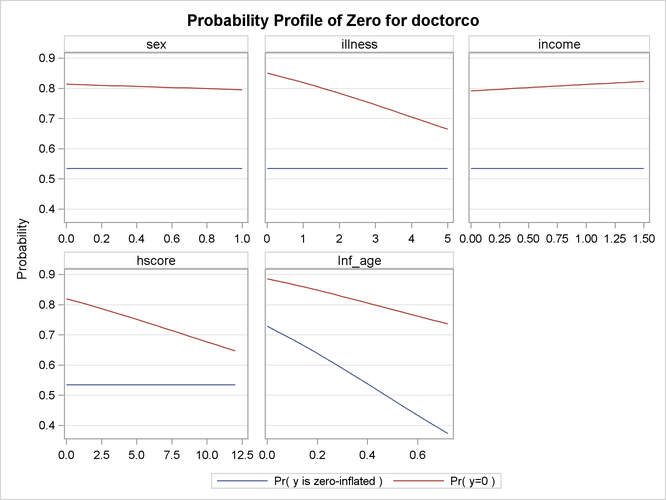
proc countreg data=docvisit plots(only)=(dispersion zeroprofile); model doctorco=sex illness income hscore / dist=zip; zeromodel doctorco ~ age; run;
You might be interested in exploring how the zero process selection probability reacts to different regressor values. Output 11.1.7 displays this information in much the same fashion as Output 11.1.3. Because Sex, Illness, Income, and Hscore do not appear in the ZEROMODEL statement, the zero-inflation selection probability does not change for different values of
those regressors. However, the plot shows that Age positively affects the zero process selection probability in a linear fashion.
In this case, the ZEROMODEL statement that follows the MODEL statement specifies that both an intercept and the variable Age be used to estimate the likelihood of zero doctor visits. Output 11.1.8 shows the resulting parameter estimates.
Output 11.1.8: Parameter Estimates for ZIP Model
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| Intercept | 1 | -1.033387 | 0.096973 | -10.66 | <.0001 |
| sex | 1 | 0.122511 | 0.062566 | 1.96 | 0.0502 |
| illness | 1 | 0.237478 | 0.019997 | 11.88 | <.0001 |
| income | 1 | -0.143945 | 0.087810 | -1.64 | 0.1012 |
| hscore | 1 | 0.088386 | 0.010043 | 8.80 | <.0001 |
| Inf_Intercept | 1 | 0.986557 | 0.131339 | 7.51 | <.0001 |
| Inf_age | 1 | -2.090924 | 0.270580 | -7.73 | <.0001 |
The estimates of the zero-inflated intercept (Inf_Intercept) and the zero-inflated regression coefficient for Age (Inf_age) are approximately 0.99 and –2.09, respectively. Because the zero-inflation model uses a logistic link by default,
you can estimate the probabilities for individuals of ages 20, 50, and 70 as follows:
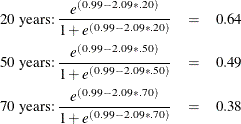
That is, the estimated probability of belonging to the low-risk group is about 0.64 for a 20-year-old individual, 0.49 for a 50-year-old individual, and only 0.38 for a 70-year-old individual. This supports the suspicion that older individuals are more likely to have a positive number of doctor visits.
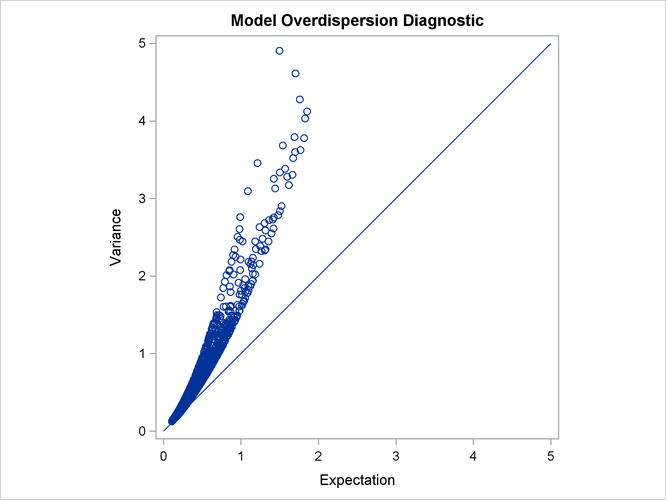
Alternative models to account for the overdispersion are the negative binomial and the zero-inflated negative binomial models, which can be fit using the DIST=NEGBIN and DIST=ZINB options, respectively.
Output 11.1.9 plots the conditional variance against the conditional mean and can be used as a diagnostic tool to check the level of overdispersion in a model.