ODS Graphics :: SAS/ETS(R) 13.2 User's Guide

ODS Graph Names

PROC SEVERITY assigns a name to each graph that it creates by using ODS. You can use these names to selectively reference the graphs. The names are listed in Table 23.18.

Table 23.18: ODS Graphics Produced by PROC SEVERITY

ODS Graph Name	Plot Description	PLOTS= Option
CDFPlot	Comparative CDF plot	CDF
CDFDistPlot	CDF plot per distribution	CDFPERDIST
PDFPlot	Comparative PDF plot	PDF
PDFDistPlot	PDF plot per distribution	PDFPERDIST
PPPlot	P-P plot of CDF and EDF	PP
QQPlot	Q-Q plot	QQ

Comparative CDF Plot

The comparative CDF plot helps you visually compare the cumulative distribution function (CDF) estimates of all the candidate distribution models and the empirical distribution function (EDF) estimate. The plot does not contain CDF estimates for models whose parameter estimation process does not converge. The horizontal axis represents the values of the response variable. The vertical axis represents the values of the CDF or EDF estimates.

If you specify truncation, then conditional CDF estimates are plotted. Otherwise, unconditional CDF estimates are plotted. The conditional estimates are computed by using the method that is described in the section Truncation and Conditional CDF Estimates.

If you specify regression effects, then the plotted CDF estimates are from a mixture distribution. For more information, see the section CDF and PDF Estimates with Regression Effects.

CDF Plot per Distribution

The CDF plot per distribution shows the CDF estimates of each candidate distribution model unless that model’s parameter estimation process does not converge. The plot also contains estimates of the EDF. The horizontal axis represents the values of the response variable. The vertical axis represents the values of the CDF or EDF estimates.

This plot shows the lower and upper pointwise confidence limits for the EDF estimates. For an EDF estimate $F_ n$ with standard error $\sigma _ n$ , they are computed as $\mbox{MAX}(0, F_ n - z_{(1-\alpha /2)} \sigma _ n)$ and $\mbox{MIN}(1, F_ n + z_{(1-\alpha /2)} \sigma _ n)$ , respectively, where $z_ p$ is the pth quantile from the standard normal distribution and $\alpha$ denotes the confidence level that you specify in the EDFALPHA= option (the default is $\alpha =0.05$ ).

If you specify truncation, then conditional CDF estimates are plotted. Otherwise, unconditional CDF estimates are plotted. The conditional estimates are computed by using the method that is described in the section Truncation and Conditional CDF Estimates.

If you specify regression effects, then the plotted CDF estimates are from a mixture distribution. For more information, see the section CDF and PDF Estimates with Regression Effects.

Comparative PDF Plot

The comparative PDF plot helps you visually compare the probability density function (PDF) estimates of all the candidate distribution models. The plot does not contain PDF estimates for models whose parameter estimation process does not converge. The horizontal axis represents the values of the response variable. The vertical axis represents the values of the PDF estimates.

If you specify the HISTOGRAM option, then the plot also contains the histogram of response variable values. If you specify the KERNEL option, then the plot also contains the kernel density estimate of the response variable values.

If you specify regression effects, then the plotted PDF estimates are from a mixture distribution. For more information, see the section CDF and PDF Estimates with Regression Effects.

PDF Plot per Distribution

The PDF plot per distribution shows the PDF estimates of each candidate distribution model unless that model’s parameter estimation process does not converge. The horizontal axis represents the values of the response variable. The vertical axis represents the values of the PDF estimates.

If you specify the HISTOGRAM option, then the plot also contains the histogram of response variable values. If you specify the KERNEL option, then the plot also contains the kernel density estimate of the response variable values.

If you specify regression effects, then the plotted PDF estimates are from a mixture distribution. For more information, see the section CDF and PDF Estimates with Regression Effects.

P-P Plot of CDF and EDF

The P-P plot of CDF and EDF is the probability-probability plot that compares the CDF estimates of a distribution to the EDF estimates. A plot is not prepared for models whose parameter estimation process does not converge. The horizontal axis represents the CDF estimates of a candidate distribution, and the vertical axis represents the EDF estimates.

This plot can be interpreted as displaying the data that are used for computing the EDF-based statistics of fit for the given candidate distribution. As described in the section EDF-Based Statistics, these statistics are computed by comparing the EDF, denoted by $F_ n(y)$ , to the CDF, denoted by $F(y)$ , at each of the response variable values y. Using the probability inverse transform $z = F(y)$ , this is equivalent to comparing the EDF of the z, denoted by $F_ n(z)$ , to the CDF of z, denoted by $F(z)$ (D’Agostino and Stephens, 1986, Ch. 4). Because the CDF of z is a uniform distribution ( $F(z)=z$ ), the EDF-based statistics can be computed by comparing the EDF estimate of z to the estimate of z. The horizontal axis of the plot represents the estimated CDF $\hat{z}=\hat{F}(y)$ . The vertical axis represents the estimated EDF of z, $\hat{F}_ n(z)$ . The plot contains a scatter plot of ( $\hat{z}$ , $\hat{F}_ n(z)$ ) points and a reference line $F_ n(z)=z$ that represents the expected uniform distribution of z. Points that are scattered closer to the reference line indicate a better fit than the points that are scattered farther away from the reference line.

If you specify truncation, then the EDF estimates are conditional, as described in the section EDF Estimates and Truncation. So conditional estimates of CDF are displayed, which are computed by using the method that is described in the section Truncation and Conditional CDF Estimates.

If you specify regression effects, then the displayed CDF estimates, both unconditional and conditional, are from a mixture distribution. For more information, see the section CDF and PDF Estimates with Regression Effects.

Q-Q Plot

The Q-Q plot is a quantile-quantile scatter plot that compares the empirical quantiles to the quantiles from a candidate distribution. A plot is not prepared for models whose parameter estimation process does not converge. The horizontal axis represents the quantiles from a candidate distribution, and the vertical axis represents the empirical quantiles.

Each point in the plot corresponds to a specific value of the EDF estimate, $F_ n$ . The Y coordinate is the value of the response variable for which $F_ n$ is computed. The X coordinate is computed by using one of the two following methods for a candidate distribution named dist:

If you have defined the dist_QUANTILE function that satisfies the requirements listed in the section <phrase remap="Argument">dist</phrase>_QUANTILE, then that function is invoked by using 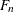$F_ n$ and estimated distribution parameters as arguments. The QUANTILE function is defined in the Sashelp.Svrtdist library for all the predefined distributions.
If the dist_QUANTILE function is not defined, then PROC SEVERITY numerically inverts the dist_CDF function at the CDF value of 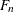$F_ n$ for the estimated distribution parameters. If the dist_CDF function is not defined, then the exp(dist_LOGCDF) function is inverted. If the inversion fails, the corresponding point is not plotted in the Q-Q plot.

If you specify truncation, then the EDF estimates are conditional, as described in the section EDF Estimates and Truncation. The CDF inversion process, whether done numerically or by evaluating the dist_QUANTILE function, needs to accept an unconditional CDF value. So the $F_ n$ value is first transformed to an unconditional estimate $F_ n^ u$ as

$F_ n^ u = F_ n \cdot (\hat{F}(t^ r_{\text {max}}) - \hat{F}(t^ l_{\text {min}})) + \hat{F}(t^ l_{\text {min}})$

where $\hat{F}(t^ r_{\text {max}})$ and $\hat{F}(t^ l_{\text {min}})$ are as defined in the section Truncation and Conditional CDF Estimates.

If you specify regression effects, then the value of the first distribution parameter is determined by using the DFMIXTURE=MEAN method that is described in the section CDF and PDF Estimates with Regression Effects.

The SEVERITY Procedure

ODS Graphics